Объединенный институт высоких температур Российской академии наук, Москва
Расширяющиеся фронты химических реакции имеют отношение к процессам в двигателях с искровым зажиганием, к проблемам предотвращения взрывов, а также таких космических явлений, как термоядерное горение в сверхновых. При воспламенении горючей смеси газов в районе точки зажигания, возникает сферическое пламя. Сразу после зажигания пламя является гладким и сферическим. С увеличением размера фронт пламени деформируется и ускоряется. Ускорение фронта пламени является сложным процессом под действием теплового расширения, различных неустойчивостей–гидродинамических, термо-диффузионных, термо-акустических и турбулентности. Когда фронт пламени достигает критического значения Pe, его ускорение становится неавтомодельным, а затем автомодельным. Величина Pe представляет собой отношение радиуса фронта пламени к толщине фронта пламени. Л.Д. Ландау показал, что пламя становится неустойчивым к возмущениям всех длин волн при Re > 1. А.Г. Истратов и В.Б. Либрович показали, что пламя становится неустойчивым при Re > 103-104. Они учитывали влияние химической кинетики, диффузии и теплопроводности и показали, что эти процессы препятствуют развитию возмущений с малой длиной волны. На сегодняшний день существует множество методов моделирования ускорения пламени, как аналитических (фрактальный подход, анализ неустойчивостей, статистический турбулентный подход Колмогорова-Обухова…) так и численных (RANS, LES, DNS…).
Работа выполнена при поддержке Российского Научного Фонда, грант №14-50-00124
Виктор Владимирович Голуб
ФГУП "ЦАГИ"
В первой части лекции, которая носит обзорный характер, приведены результаты исследований гиперзвуковых течений вязкого газа начиная с середины XX века. Обсуждаются особенности течений для различных режимов вязко-невязкого взаимодействия, которые были установлены в экспериментальных работах Борового В.Я., Майкапара Г.И., Whitehead A.H., Hefner J.N., Rao D.M., Cross E.J. и др. Для режима сильного взаимодействия приведены автомодельные решения: Lees L.J. – Stewartson K. - обтекания полубесконечной пластины, Whalen R.J. - скользящей пластины и Ладыженского М.Д. - плоских треугольных крыльев. Далее обсуждаются вопросы, связанные с распространением возмущений против потока, которое впервые в 1970 году было установлено Нейландом В.Я. [1, 2]. Приведены результаты исследований Stewartson K. обтекания пластины с учетом решения уравнений для ударного слоя, а также решения Михайлова В.В., Нейланда В.Я., Дудина Г.Н. для обтекания треугольных крыльев на режиме сильного взаимодействия.
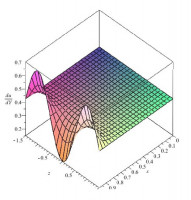
Во второй части лекции обсуждается вопрос о возможности образования пространственного течения на пластине конечной длины на режиме сильного взаимодействия. В предположении, что на задней кромке пластины задается дополнительное условие, которое является функцией от поперечной координаты и, учитывая вид первых членов разложения для функций течения в окрестности передней кромки [3], сформулированы и решены краевые задачи для определения следующих членов разложения. Впервые показано, что для функций течения p(x, z), δ(x, z), u(x, Y, z), ν(x, Y, z), H(x, Y, z) эти члены имеют порядок O( (pα(z)/p0)2 x2α), а для w(x, Y, z) - O( dpα(z)/dz (pα(z)/(p0)2) x2α+1), где α - собственное число и pα(z) - произвольный параметр. Установлено, что возникающее вторичное течение в сечениях пропорционально величине dpα(z)/dz.
На рисунке приведена зависимость du/dY на поверхности пластины, которая пропорциональна коэффициенту продольного трения, при температурном факторе Hw=1.5 и параметре pα(z)=0.2 cos(πz).
Рассмотрено также обтекание скользящей пластины. Установлено принципиальное отличие от предыдущего случая. Уравнение для w(x, Y, z) не отделяются от основной системы уравнений, а самое главное, третьи члены разложений имеют порядок O( (dpα(z)/dz) xα+1). Таким образом, при наличии угла скольжения, влияние третьего члена разложения на распространений возмущений существенно больше, чем при отсутствии скольжения. Установлено, что увеличение угла скольжения приводит к значительному уменьшению значений собственного числа.
Работа выполнена при финансовой поддержке РФФИ (проект № 18-01-00211).
1. Нейланд В.Я. Распространение возмущений вверх по течению при взаимодействии гиперзвукового потока с пограничным слоем // Изв. АН СССР. МЖГ. 1970. № 3. С. 40-49.
2. Нейланд В.Я., Боголепов В.В., Дудин Г.Н., Липатов И.И. Асимптотическая теория сверхзвуковых течений вязкого газа. – М.: Физматлит, 2003. – 456 с.
3. Дудин Г.Н., Нейланд В.Я. Об индуцировании трехмерных возмущений в пограничном слое при сильном взаимодействии с гиперзвуковым потоком // Изв. РАН. МЖГ. 2018. № 1. С. 89-96.
Георгий Николаевич Дудин
Вычислительный центр им. А.А. Дородницына ФИЦ ИУ РАН
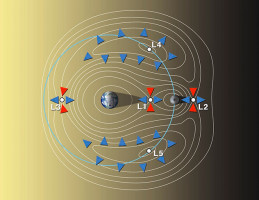
В классической ограниченной плоской круговой задаче трех тел существует пять точек либрации, в которых уравновешиваются силы притяжения к основным телам и центробежная сила, возникающая за счет вращения системы отсчета, связанной с основными телами. Две из этих точек – треугольные лагранжевы точки либрации – устойчивы по Ляпунову в достаточно широком диапазоне отношений масс основных тел. В окрестности этих точек естественно ожидать скопления космической материи. В системе Солнце-Юпитер зафиксировано порядка десяти тысяч таких космических тел – троянских астероидов. Кроме троянцев Юпитера известны троянцы Земли, Марса, Урана и Нептуна.
Подобные скопления астрономы пытались обнаружить и в треугольных точках либрации системы Земля-Луна. Впервые наличие сгущения космической массы в этих точках было зарегистрировано польским астрономом Кордылевским более полувека назад. Однако, после Кордылевского многие астрономы пытались повторить эти наблюдения, и в большинстве случаев их попытки оказывались безуспешными. Дискуссия о «неуловимых облаках Кордылевского» не утихает до сих пор.
Как показало теоретическое исследование, феномен «появления и исчезновения» облаков Кордылевского объясняется существенным влиянием на движение частиц гравитационных сил и сил светового давления, действующих со стороны Солнца. При учете этих сил треугольные точки либрации системы Земля-Луна уже не будут точками равновесия всех действующих сил. Частица, помещенная в треугольную точку либрации без начальной относительной скорости быстро покидает окрестность этой точки. Вместо точек равновесия возникают устойчивые периодические движения с периодом в один синодический месяц, равный промежутку времени между двумя новолуниями (29дн. 12час. 44мин.).
В теоретическом исследовании мы рассматривали ограниченную плоскую круговую задачу четырех тел Земля-Луна-Солнце-частица: Земля и Луна движутся по круговым орбитам вокруг их общего центра масс, который, в свою очередь, движется по круговой орбите вокруг Солнца. Показано существование устойчивых периодических орбит, охватывающих треугольные точки либрации: каждая из двух симметричных треугольных точек либрации охватывается двумя устойчивыми периодическими орбитами. Одна из орбит показана на правом рисунке (внутренняя орбита), цифры означают фазы Луны с интервалом 1/8 синодического месяца. Устойчивость по Ляпунову этих орбит обусловливает возможность наличия в окрестности точки, движущихся по периодической орбите, скопления частиц, движущихся по близким возмущенным орбитам. Эти частицы могут составлять в общей совокупности четыре облака Кордылевского.
Для успешного наблюдения этих облаков нужно знать точное место их нахождения на небосводе и время для наблюдения. Появление облака на линии визирования треугольной точки либрации соответствует вполне определенному периоду синодического месяца, сдвинутому относительно момента новолуния на фиксированный отрезок времени вперед или назад в зависимости от выбора одной из двух треугольных точек либрации. Показано, что именно этот период отвечает наилучшим условиям наблюдения: минимальному расстоянию от Земли и наилучшему освещению Солнцем. Кроме того, для наблюдения необходимо, чтобы в данной местности расчетный период времени приходился на ночь и чтобы точка либрации находилась выше горизонта, а Луна находилась ниже горизонта. Одновременное выполнение этих условий осуществляется не каждый месяц и требует дополнительных расчетов. Проведенные расчеты подтвердились известными из астрономической литературы датами успешных наблюдений. Эти трудности объясняют кажущийся «феномен появления и исчезновения» облаков Кордылевского.
Интересно было выяснить структуру распределения плотности частиц внутри облака Кордылевского. Для этого было численно проинтегрировано уравнение в частных производных Лиувилля для определения плотности вероятности распределения координат и скоростей частиц в шестимерном фазовом пространстве с последующим агрегированием решения по скоростям. Полученные распределения качественно совпали с фотографиями, полученными Кордылевским.
Что касается силы светового давления, то она также как и гравитационная сила обратно пропорциональна расстоянию частицы от Солнца, поэтому эффект светового давления сводится к редукции коэффициента притяжения к Солнцу. С другой стороны, сила светового давления пропорциональна площади Миделя частицы ортогональной направлению солнечных лучей, пропорциональной квадрату характерного линейного размера частицы, а гравитационная сила пропорциональна массе частицы, которая при постоянной плотности пропорциональна кубу линейного размера частицы. Отсюда следует, что эффект светового давления увеличивается обратно пропорционально линейному размеру частицы. При учете светового давления мы получаем семейство периодических траекторий, рождающегося из периодических траекторий, соответствующих отсутствию светового давления.
При определенном микроскопическом размере пылевых частиц действие гравитационных и световых сил уравновешивается, и мы приходим к классической невозмущенной задаче трех тел. Отдельно был рассмотрен этот особый случай микроскопических пылевых частиц. Однако, микроскопические космические частицы обычно оказываются электрически заряженными, и для них существенную роль играют электростатические силы взаимодействия, т.е. необходимо рассматривать уравнение движения плазмы – интегро-дифференциальное уравнение в частных производных Власова. Исследование показало наличие периодически изменяющихся устойчивых пульсирующих и неравномерно вращающихся форм облаков заряженных частиц в окрестности треугольных точек либрации.
Работа выполнена при частичной поддержке грантов РФФИ №15-01-03747 и №16-01-00625.
1. Salnikova T.V., Stepanov S.Ya., Anna Shuvalova A.I. Three-body problem for the Earth-Moon system under photo-gravitational influence of the Sun // Advances in the Astronautical sciences, 2018, vol. 161, pp. 201-208
2. Сальникова Т.В., Степанов С.Я. Математическая модель образования космических пылевых облаков Кордылевского // Доклады Академии наук, Наука (М.), 2015, том 463, № 2, с. 164-167
Сергей Яковлевич Степанов
ЦАГИ имени проф. Н.Е. Жуковского, Жуковский, Моск. обл.
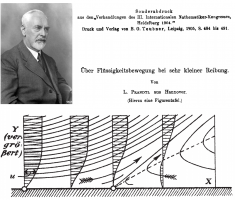
В докладе представлены исторические аспекты создания новых направлений в механике и в математике, связанные с новым подходом к исследованию проблем, содержащих малый параметр (или малые параметры). Эти подходы во многом связаны с именем Людвига Прандтля, создавшего как теорию пограничного слоя, так и методологию решения многих других задач с использованием асимптотических методов. Кроме истории создания этой теории представлены также и результаты, полученные в течение последующих 100 лет после публикации ключевой работы Прандтля. Обсуждаются перспективы дальнейших исследований, а также достигнутые результаты в области изучения устойчивости и перехода ламинарного пограничного слоя.
Рис. Сверху - Людвиг Прандтль и его труд «О движении жидкости с малым трением», 1904 г., снизу - пограничный слой на пластине (из работы Прандтля 1904 г.)
Игорь Иванович Липатов
Институт проблем механики им. А.Ю. Ишлинского РАН
Несмотря на то, что космическое пространство заполнено очень разреженным газом, для построения моделей физических явлений, встречающихся в космосе, часто используются методы гидроаэромеханики и магнитной гидродинамики. Это обусловлено, во-первых, тем, что обычно характерные масштабы этих явлений очень велики, а длины свободного пробега часто оказываются малыми по сравнению с ними. Во-вторых, космическое пространство заполнено в основном ионизованным газом, т.е. газом, который находится в состоянии плазмы. В последнем случае длины свободного пробега могут определяться не только парными кулоновскими столкновениями между заряженными частицами, но и так называемыми «коллективными» процессами, при которых длины свободного пробега существенно меньше длин свободного пробега в парных столкновениях, что дает возможность построения гидродинамических моделей. Активное развитие теоретических моделей тех явлений, которые встречаются в космическом пространстве, началось после того, как космические аппараты вышли в открытый космос, а приборы, устанавливаемые на них, смогли проводить прямые измерения гидродинамических параметров (скорости, плотности, температуры). Кроме того, появилась возможность исследования удаленных астрофизических явлений во всем диапазоне длин волн. Это, конечно, накладывает особую ответственность на ученых, занятых построением теоретических моделей, поскольку ценность модели определяется экспериментальным подтверждением ее выводов.
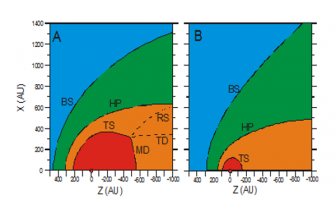
В настоящем докладе будут затронуты две проблемы, к которым автор имеет самое непосредственное отношение, а именно, взаимодействие солнечного ветра с межзвездной средой, окружающей солнечную систему, и с кометными атмосферами. Обе проблемы сводятся к газодинамическому или магнитогидродинамическому (МГД) взаимодействию двух сверхзвуковых потоков, в которых происходят химические реакции (процессы перезарядки, фотоионизации, ионизации электронным ударом и др.). Запуск космических аппаратов (КА) Voyager – 1, Voyager – 2, Pioneer – 10, Pioneer – 11 в середине 70-х годов прошлого столетия для изучения удаленных областей солнечной системы придал особую актуальность первой проблеме. Автору доклада вместе с сотрудниками и коллегами удалось построить пионерские модели с образованием двух ударных волн (в солнечном ветре и в межзвездной плазме) и тангенциального разрыва, разделяющего оба потока. В частности, в работе [1] впервые была предложена модель в ньютоновском приближении тонкого слоя. которая дала толчок к созданию реальной модели, учитывающей главный процесс резонансной перезарядки атомов Н, проникающими из межзвездной среды в солнечный ветер, с протонами [2]. Многие физические явления, предсказанные в модели [2], были через много лет подтверждены экспериментами на КА. В частности, на Рис. 1 приведены данные расчета формы и положения сильных разрывов, полученные в этой работе. Аппараты Voyager – 1 и Voyager – 2 пересекли ударную волну торможения солнечного ветра в 2004 и 2007 году на расстояниях 84 а.е. и 94 а.е., соответственно, что, с точностью ~ 3%, совпадает с предсказанным положением этой ударной волны (TS).
Для понимания процессов, которые происходят при взаимодействии солнечного ветра с кометными атмосферами, важным моментом были миссии космических аппаратов Вега – 1, Вега – 2, Giotto, Suissei и Sakigakе к комете Галлея в марте 1986 года и аппарата Rosetta к комете Чурюмова – Герасименко (2014 – 2016 годы). Пионерская работа по созданию гидродинамической модели в этой проблеме принадлежит авторам работы [3]. Применительно к исследованию кометы Галлея в марте 1986 года качественная модель в [3] была численно решена в работе [4], результаты которой хорошо совпали с данными экспериментов на космических аппаратах. В дальнейшем авторами работ [5 – 7] была развита МГД модель взаимодействия солнечного ветра с атмосферами комет Галлея, Григга – Шеллерупа и Чурюмова – Герасименко во время прохождения этих комет через перигелий.
Рисунок: Результаты численной модели взаимодействия солнечного ветра и межзвёздной звезды (Baranov and Malama, JGR, 1993). Левый рисунок не учитывает процесс резонансной перезарядки. Правый рисунок учитывает этот важный в проблеме эффект.
Автор выражает благодарность гранту РФФИ № 16-01-00305 за частичную финансовую поддержку доклада.
[1] Баранов В.Б., Краснобаев К.В., Куликовский А.Г., ДАН СССР, т. 194, стр. 41, 1970,
[2] Baranov V.B., Malama Yu.G., J. Geophys. Res., v. 98, pp. 15157 – 15163, 1993.
[3] L. Biermann, B. Brosowski, and H.U. Schmidt, Solar Phys., v. 1, p. 254, 1967
[4] Баранов В.Б., Лебедев М.Г., Письма в АЖ, т.. 12, стр.. 551, 1986
[5] Алексашов Д.Б., Баранов В.Б, Лебедев, Известия РАН, МЖГ, № 1, 2015
[6] Baranov V.B., Alexashov D.B., Lebedev M.G., MNRAS, v. 449, pp. 2268–2273, 2015
[7] Lebedev M.G., Baranov V.B., Alexashov D.B., Earth, Moon and Planets, v. 116, pp. 159 – 179, 2015
Баранов Владимир Борисович
Санкт-Петербургский Политехнический университет Петра Великого
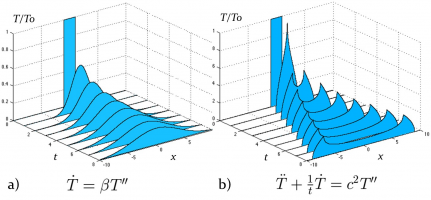
В докладе излагаются подходы и приложения механики дискретных сред. Рассматриваются задачи, в которых проявляется нарушение континуальности среды – или в силу дискретности структуры вещества, или в силу особенности протекающих в нем процессов. Подробно рассматриваются задачи, связанные с описанием аномальных тепловых процессов на микроуровне: немонотонной тепловой релаксации, тепловой сверхпроводимости и др. Предлагаются подходы, позволяющие в простейших случаях на основе уравнений динамики частиц вещества получить аналитическое описание указанных процессов. Проводится сравнение эволюции теплового возмущения при обычной теплопроводности (рис. 1а) и тепловой сверхпроводимости (рис. 1b). Показывается, что тепло в сверхпроводящих системах может распространяться со скоростью, близкой к скорости звука, что открывает возможность для перспективных практических приложений.
Рисунок: сравнение эволюции теплового возмущения при обычной теплопроводности (рис. 1а) и тепловой сверхпроводимости (рис. 1b).
Список литературы:
1. А.М. Кривцов. Распространение тепла в бесконечном одномерном гармоническом кристалле. Доклады Академии Наук. 2015, том 464, № 2, C. 162-166. (English version: Krivtsov A. M. Heat transfer in infinite harmonic one dimensional crystals. Doklady Physics, 2015, Vol. 60, No. 9, pp. 407–411.)
Кривцов Антон Мирославович
Центральный Институт Авиационного Моторостроения (ЦИАМ), Москва
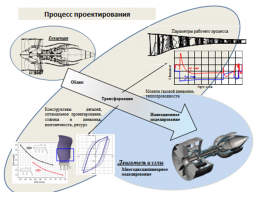
Авиационные двигатели – высоконагруженные конструкции энергетического машиностроения, процесс проектирования которых требует применения современных методов и алгоритмов многодисциплинарного математического моделирования объединяющих в единую стратегию «Виртуального двигателя» [1] модели газовой динамики, теплопроводности и механики деформируемого твердого тела. Актуальность такого подхода основана на необходимости сокращения объемов дорогостоящих натурных испытаний деталей, узлов и конструкций. Кроме этого, технология многодисциплинарного моделирования позволяет, при наличии моделей различного уровня, обеспечить как распознавание и восполнение объемов информации, получаемой в натурных экспериментах, так и проведение вычислительных экспериментов, позволяющих исследовать поведение конструкций в экстремальных условиях.
Методически процесс проектирования двигателя и его узлов может быть разбит на три стадии: создания облика конструкции (область дивергенции), проектирования деталей и узлов (область трансформации) и имитационного моделирования (область конвергенции) [1]. На первой стадии определяются условия и требования, которые позволяют вести на последующих стадиях автономную работу над отдельными узлами и деталями параллельно. При этом на каждой из стадий проектирования деталей и узлов двигателя необходимо применять математические модели различного уровня, однако следует соблюдать требования информационного единства и информационной взаимосвязи между моделями газовой динамики, теплопроводности и механики твердого тела. Отметим, что информационное единство и взаимосвязь между математическими моделями определяются граничными и начальными условиями, которые во многих случаях являются вычисляемыми. Это важно для стадии имитационного моделирования, на которой необходимо применять модели наиболее приближенные к условиям работы детали, узла или двигателя, что позволяет получить окончательные оценки рабочих параметров двигателя, кинетики теплового и напряженно-деформированного состояния деталей в рабочем цикле, прогнозировать ресурс и надежность конструкции. В лекции рассмотрены принципы создания моделей многодисциплинарного моделирования и приведены примеры применения стратегии «Виртуальный двигатель» на различных стадиях проектирования узлов и деталей.
На стадии концептуального проектирования – формирования облика конструкции определенное место занимают экспертные базы знаний, обобщающие существующий опыт создания двигателей и тенденции развития технологий производства материалов, деталей и узлов, математические модели прогноза развития технологий, потребностей рынка на ряд лет вперед, методы экспресс оптимизации при ограниченном объеме информации. Несмотря на то, что стоимость этого этапа в общих затратах на разработку двигателя невелика, его реализации необходимо уделять большое внимание, так как ошибка в прогнозе может привести к проблеме успешной реализации проекта. Следует отметить, что эта часть процесса проектирования требует участия специалистов с наиболее высокой квалификацией.
Так как авиационный двигатель хорошо структурированная конструкция, проектирование его деталей и узлов происходит на стадии трансформации параллельно в различных подразделениях, при условии, что разрабатываемые проекты не выходят за рамки общих ограничений установленных на стадии концептуального проектирования. При этом определенное место занимают «быстрые алгоритмы», основанные на одновременном применении средств вычислительной механики и оптимизации при проектировании лопаток компрессора и турбины, дисков и роторов, опор и силовой схемы двигателя. На этой стадии существенно качество моделей и алгоритмов газовой динамики, теплопроводности и структур-ного анализа, моделей поведения материалов, моделей прогноза ресурса и надежности [2]. Ряд примеров применения таких алгоритмов приведен в докладе.
На стадии конвергенции применяют модели, наиболее адекватно описывающие физические процессы в деталях и узлах двигателя. Это позволяет оценить поведение конструкции на всех этапах рабочего цикла, учесть возможные ресурсные явления, моделировать аварийные ситуации и т.д. В докладе приведен пример математического моделирования кинетики теплового и напряженно-деформированного состояний ротора компрессора с использованием термомеханической модели, объединяющей совместную работу модулей газовой динамики, описывающих вторичные течения в полостях, модулей расчета теплового состояния деталей и модуля изменения напряжений и деформаций конструкции. Также в докладе рассмотрены:
- технологии «Виртуального двигателя» при моделирования нелинейных колебаний систем ротор-корпус, зубчатых колес редукторов и трансмиссий, уплотнений с учетом эффектов контактного взаимодействия деталей. Показано, что наибольший эффект может быть получен при предварительном анализе трехмерных задач расчета статики и динамики узлов и редукции этих задач к адекватным «быстрым моделям» «балочного типа»;
- принципы построения моделей пластичности, ползучести и ресурса применительно к задачам неизотермического циклического деформирования высоконагруженных деталей ГТД;
- принципы построения систем автоматизированного и оптимального проектирования дисков и лопаток ГТД. Определенное внимание уделено разработке систем взаимодействующих с конструктором в диалоговом режиме;
- перспективы применения быстрых алгоритмов МКЭ и МГЭ для решения физически и геометрически нелинейных задач деформирования деталей ГТД; принципы построения вычислительных комплексов, в которых взаимодействуют модули, работающие с моделями различного уровня и принципы управления потоками информации.
Вопросы технологии «Виртуального Двигателя» рассмотрены в ряде глав работы [1] и в других публикациях [2-5].
1. Скибин В.А., Солонин В.И, Темис Ю.М. в кн. Машиностроение. Энциклопедия/ Ред. Совет К.В. Фролов (пред.) и др. – М.: Машиностроение. Самолеты и вертолеты. Т. IV-21/ Авиационные двигатели. Кн.3 / В.А. Скибин, В.И. Солонин, Ю.М. Темис и др.; под ред. В.А. Скибина, Ю.М. Темиса и В.А. Сосунова. – 2010. – 720 с.
2. Temis Y.M.,. Selivanov A.V, Yakushev D.A. “Virtual Engine” Approach for the Coupled Analysis of Engine Struc-ture, Proc. 23rd ISABE Conference, Manchester, UK, 3-8 Sep. 2017, Paper ISABE-2017-22645.
3. Темис Ю.М., Якушев Д.А. Оптимальное проектирование конструктивных элементов ГТД. Техника воздушного флота, №1(694) М.: ЦАГИ, 2009. С. 54-64.
4. Темис Ю.М., Якушев Д.А., Алхимов Д.А. Проблемы оптимального проектирования деталей ГТД // III Меж-дународный технологический форум «Инновации. Технологии. Производство»: Сборник материалов мини-конгресса Центрального института авиационного моторостроения имени П.И. Баранова «Математическое мо-делирование и проектирование в авиадвигателестроении» / Под ред. д.т.н., проф. Ю.М. Темиса. – Рыбинск: РГАТУ имени П. А. Соловьева, 2016. – С. 11-24.
5. Бондарь В.С., Алхимов Д.А., Факеев А.И., Темис Ю.М., Якушев Д.А., Пестов А.В. Система автоматизированного проектирования роторов ГТД. // Известия МГТУ «МАМИ». Естественные науки. М., МГТУ «МАМИ», № 1(23), 2015. Т. 4. С. 10–20.
Темис Юрий Моисеевич
Институт проблем механики им.А.Ю.Ишлинского РАН, Москва
Изнашивание есть удаление материала с поверхности трения вследствие ее разрушения, проявляющееся в постепенном изменении формы и размеров взаимодействующих тел. Изнашивание машин и механизмов приводит к ухудшению работы сопряжений и выходу их из строя.
При моделировании разрушения поверхностных слоёв элементов трибосопряжений используются методы и модели механики контактного взаимодействия и разрушения c учетом ряда специфических свойств, выделяющих изнашивание в особый вид разрушения. Специфика износа заключается, прежде всего, в том, что сам факт протекания этого процесса не является критическим для работы сопряжения. Обычно допустимый износ подвижных элементов сопряжений намного больше характерного размера частицы износа [1], поэтому при работе сопряжений имеет место многократно повторяющееся отделение частиц материала с поверхности трения. Свойства (микрогеометрия, степень поврежденности и т.д.) оставшегося материала зависят от истории процесса фрикционного взаимодействия, т.е. изнашивание является процессом наследственного типа. Кроме того, изнашивание есть процесс с обратной связью. Процессы самоорганизации и формирования равновесных структур при изнашивании являются проявлением действия обратной связи [2].
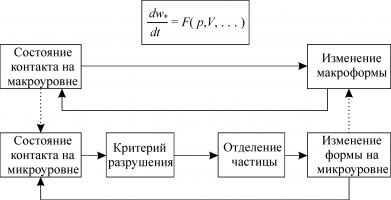
Модели изнашивания обычно рассматриваются на двух масштабных уровнях (см. рисунок): макроуровень, определяющий кинетику изменения макроформы тел при изнашивании, и микроуровень, описывающий каждый элементарный акт отделения частицы с поверхности [3]. Многократное повторение расчетов на микроуровне позволяет оценить изменение характеристик сопряжения на макроуровне (изменение макроформы, сближение тел при изнашивании и т.д.) и рассчитать долговечность сопряжения по критериям износостойкости.
Рисунок - Основные этапы моделирования изнашивания и их взаимосвязь.
При построении модели изнашивания на микроуровне (нижняя часть рисунка) необходимо, прежде всего, определить физический механизм отделения частицы износа с поверхности трения. К числу наиболее распространенных механизмов изнашивания, проявляющихся в условиях фрикционного взаимодействия поверхностей, относятся абразивное, адгезионное, усталостное, коррозионно-механическое и т.д. В соответствии с установленным механизмом изнашивания выбирается критерий разрушения, рассчитываются напряженное состояние и температура поверхностных слоев, возникающие вблизи поверхности при заданных условиях контактного взаимодействия, а также другие характеристики, входящие в критерий разрушения. После этого с использованием методов и подходов механики разрушения моделируется отделение частицы и определяются новые характеристики поверхностного слоя [3,4]. Этот подход, в частности, применяется для моделирования контактно-усталостного разрушения колес и рельсов в условиях трения качения [5,6].
Анализ процессов, протекающих на микроуровне, позволяет разработать феноменологическую модель изнашивания пары трения на макроуровне (верхняя часть рисунка), определяющую зависимость скорости износа dw*/dt от макрохарактеристик контакта, таких как контактное давление p, скорость V относительного перемещения поверхностей, температура и т.д. Вид этой функции зависит от процесса, протекающего на микроуровне, и определяется на базе моделирования элементарных актов разрушения и отделения частиц износа с поверхности трения [7].
С целью расчета ресурса трибосопряжений на макроуровне разработаны общие методы анализа контактной задачи с учетом формоизменения тел при изнашивании. Эта задача в общем случае описывается системой уравнений эволюционного типа. Определены необходимые условия существования установившегося режима изнашивания. Этот режим особенно важен, поскольку основная доля ресурса сопряжения приходится на установившийся режим, который характеризуется формированием стационарной формы и стационарным (или квазистационарным при растущей области контакта) распределением давлений [8]. На основании построенных моделей процесса изнашивания ставится и решается обратная задача управления параметрами структуры поверхностей с целью оптимизации процесса изнашивания (например, минимизации времени приработки, обеспечения требуемой формы изношенной поверхности и т.д.) [3]. Построено также численно-аналитическое решение износоконтактной задачи в условиях осциллирующих нагрузок при неполном проскальзывании в области контактного взаимодействия (фреттинг-износ) [9].
Разработанные методы решения износоконтактных задач используются для расчета кинетики изменения при изнашивании контактных характеристик (контактного давления, сближения взаимодействующих поверхностей, размера области контакта и т.д.) многих трибосопряжений – подшипников скольжения, зубчатых передач, направляющих скольжения, уплотнений [10,11]. Исследование износоконтактных задач позволяет также разработать методы управления процессами изнашивания различных трибосопряжений.
Исследование выполнено при финансовой поддержке Программы Президиума РАН I.16 «Развитие физико-химической механики поверхностных явлений как фундаментальной основы для разработки современных конструкций и технологий».
1. Крагельский И.В., Добычин М.Н., Комбалов В.С. Основы расчетов на трение и износ. - М.: Машиностроение, 1977, 576 с.
2. Буше Н.А., Копытко В.В. Совместимость трущихся поверхностей. – М.: Наука, 1981, 128 с
3. Горячева И.Г. Механика фрикционного взаимодействия. – М. Наука, 2001, 478 с.
4. Горячева И.Г., Торская Е.В. Моделирование накопления контактно-усталостных повреждений и усталостного износа // Сб. научн. тр. “Трибология. Состояние и перспективы” / Под. ред. И.Г. Горячевой и М.А. Броновца. 2016, Уфа: РИК УГАТУ, Т.1. 134–147
5. Goryacheva I, Zakharov S. Rolling contact fatigue defects in freight car wheels // Wear., 2005, V. 258. № 78. P. 11421147
6. Контактно-усталостные повреждения колес грузовых вагонов. / Под ред. С.М. Захарова. М.: Интекст, 2004, 160 с.
7. Горячева И.Г., Чекина О.Г. Изнашивание поверхностей: от моделирования микроразрушения к анализу формоизменения. // Изв.РАН. МТТ. 1999. № 5, С. 131-147
8. Горячева И.Г., Добычин М.Н. Контактные задачи в трибологии. – М. Машиностроение, 1988, 254 с.
9. Горячева И.Г., Горячев А.П. Износоконтактная задача с неполным проскальзыванием // ПММ. 2006, Т. 70. Вып. 6. С. 10421053
10. Goryacheva I.G. Contact Mechanics in Tribology. Dordrecht: Kluwer, 1998, 344 p.
11. Солдатенков И.А. Износоконтактная задача с приложениями к инженерному расчету износа. М. Физматкнига, 2010, 160 с.
Ирина Георгиевна Горячева
Центральный институт авиационного моторостроения имени П.И. Баранова
Выполнено сравнение термических коэффициентов полезного действия и удельных тяг и импульсов прямоточных реактивных двигателей разных типов с медленным ("дефлаграционным") горением (МГ) и с горением в движущихся (пульсирующих и вращающихся – «спиновых») и неподвижных детонационных волнах (ДВ). Актуальность такого сравнения обусловлена распространенными, особенно в последнее время, утверждениями о возможном увеличении тяговых характеристик воздушно-реактивных двигателей (ВРД) с горением в ДВ (в первую очередь, в пульсирующих – PDE и вращающихся – RDE) на десятки процентов в сравнении с прямоточными ВРД (ПВРД) с МГ при постоянном давлении в дозвуковом потоке. Подобные прогнозы, однако, опираются не на прямой расчет тяг этих двигателей, а на сравнение их идеальных термических коэффициентов полезного действия (кпд) – hth и на применимые только к стационарным течениям в инерциальных системах координат формулы, связывающие также идеальные удельные тяги и импульсы с идеальными кпд. Для PDE эти формулы неверны из-за нестационарности течения.
В России утверждения о преимуществах детонационного горения (ДГ) нередко сопровождаются ссылками на заметку Я.Б. Зельдовича [1] 1940 г., переведенную на Западе только в начале XXI века. Для незнакомых с этой заметкой ссылки на столь авторитетного ученого производят требуемый эффект в противоположность тому, что писал сам автор. Хотя Я.Б. Зельдович обнаружил некоторое увеличение термического коэффициента полезного действия (КПД) при ДГ, это не вызвало у него эйфории. Напротив, в той же заметке высказаны только скептические соображения о применении ДГ, например: "... поиски циклов с ДГ в погоне за небольшим увеличением принципиально достижимого кпд бесперспективны". Ни в этой, ни в других публикациях Я.Б. Зельдовича высказываний в поддержку ДГ нет.
В развитие [1, 2] выполнен термодинамический анализ разных типов ВРД с ДГ и МГ. В исследуемых далее ВРД горению почти всегда предшествует сжатие в воздухозаборнике поступающего из атмосферы со скоростью V0 воздуха и всегда заканчивается "расчетным" расширением в сопле продуктов сгорания до давления набегающего потока р0. В рассматриваемых моделях двигателей предварительное сжатие воздуха в воздухозаборнике и расширение продуктов сгорания в сопле принимаются изэнтропическими и стационарными. По определенным, как в [2], идеальным термическим кпд (hth) находится отношение Ve/V0, где Ve – скорость на выходе из сопла при расчетном расширении до р0. Удельные тяга и импульс пропорциональны разности (Ve/V0 – 1). Рассмотренные типы ВРД включают двигатели с МГ при постоянном давлении, как в ПВРД (по циклу Брайтона), и постоянном объеме (по циклу Хэмфри), пульсирующие детонационные двигатели (PDE) с горением в ДВ Чепмена - Жуге (ДВCJ), ВРД с горением в стационарных ДВCJ, в том числе, с предварительным торможением сверхзвукового потока (SDEy³1, y = Т3/Т0, Т0 и Т3 – температуры холодного воздуха и горючей смеси перед ДВ) и в косой ДВ – SDEOSW (при y = 1).
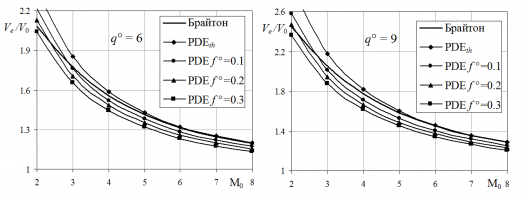
При фиксированных показателях адиабаты воздуха, горючей смеси и продуктов сгорания идеальные характеристики рассмотренных ВРД, предполагающие, как в [2], отсутствие потерь при торможении воздуха в воздухозаборнике, его смешении с газообразным топливом и истечении продуктов сгорания из реактивного сопла, зависят от двух безразмерных параметров: числа Маха полета М0 и q° = q/(cpT0) – безразмерной теплотворной способности горючей смеси (ср – теплоемкость при постоянном давлении). При q° = 6 и 9 сравнение идеальных кпд hth и рассчитанных по hth с помощью упомянутых выше формул (незаконных для PDE) идеальных удельных тяг и импульсов всех рассмотренных двигателей выполнено для М0 от 0.3 до 8. Для этих q° и М0 по такой идеальной тяге PDE незначительно превосходит ВРД с горением при постоянном объеме (по циклу Хэмфри), а ПВРД с МГ – намного только при М0 < 1.5. С ростом М0 превышение идеальной тяги PDE над идеальными тягами других ВРД за исключением SDEOSW быстро уменьшается. Так, при q° = 6 и 9 превосходство по идеальной тяге PDE над остальными становится малым при увеличении числа Маха полета М0.
Пусть PDE имеет n цилиндрических, синхронно работающих групп детонационных камер (ДК) с мгновенно открывающимися и закрывающимися клапанами (входными силовыми стенками). При открытых клапанах в ДК поступает идеально перемешанная горючая смесь. Период работы одной ДК PDE можно разбить на несколько этапов: 1. Открытие клапана, заполнение ДК горючей смесью, мгновенные закрытие клапана и инициирование ДВ волны у входного конца ДК; 2. Приход ДВ на правый конец ДК – сечение входа в идеально регулируемое реактивное сопло; 3. ДВ отражается от правого частично открытого сечения ДК (сужения сопла) как ударная волна (УВ), которая движется к закрытому входному сечению ДК. Далее нестационарные ударные волны, двигаясь по ДК, могут несколько раз отразиться от ее концов. Несмотря на затухание, отражающиеся УВ – не учитываемый при определении идеальных характеристик PDE источник роста энтропии. Клапан мгновенно открывается, когда среднее давление продуктов сгорания в ДК становится меньше давления заторможенного воздуха и идеально перемешанного с ним топлива в объеме перед клапаном.
Истечение продуктов сгорания происходит на протяжении всего цикла работы PDE. Течение в расширяющейся части сопла квазистационарное и изэнтропическое, площадь выходного сечения сопла идеально регулируемая. Расчёты проводились в рамках одномерной задачи в приближении уравнений Эйлера. Система уравнений одномерной нестационарной газовой динамики численно решалась с помощью явной монотонной распадной разностной схемы второго порядка (для гладких решений) по пространственной координате х и по времени t. Второй порядок по времени обеспечивался привлечением схемы Рунге - Кутты. При заданных f ° (отношении площади критического сечения сопла к площади поперечного сечения ДК), М0 и q° в течении периода работы ДК PDE отношение скоростей Ve/V0 получается как функция времени. Его интегрирование по периоду дает средние значения Ve/V0 и тяговые характеристики с учетом нестационарности и неизэнтропичности течения продуктов сгорания в детонационной камере.
На рисунке приведены кривые отношений Ve/V0 для ПВРД (цикл Брайтона, от времени не зависит) и для PDE: посчитанных по идеальному термическому кпд (PDEth) и для нескольких значений f °, найденных в рамках описанной выше нестационарной модели. Видно, что в типичных ситуациях ПВРД лучше многокамерных PDE с вращающимся клапаном (для f °= 0.3 и 0.1 – при М0 ³ 2 и М0 ³ 3). Согласно [3] тяговые характеристики ПВРД заведомо лучше тяговых характеристик и однокамерного PDE, предложенного в [4]. По этим характеристикам уступают ПВРД и все рассмотренные выше ВРД с горением в стационарных ДВ. Из еще не рассмотренных "детонационных" ВРД в последнее время особое внимание уделяется двигателям с вращающейся или спиновой ДВ (RDE). Одно из объяснений такого внимания – переход к стационарному течению во вращающейся со скоростью ДВ системе координат и последующие рассуждения с сохраняющейся в стационарных потоках полной энтальпией. При этом, правда, забывают, что в координатах, вращающихся с угловой скоростью w, вдоль линий тока сохраняется не "обычная" полная энтальпия H, а разность H °= H – (wr)2/2. В кольцевой камере сгорания RDE произведение wr равно скорости детонационной волны. Поэтому величина w так велика, что любые изменения радиальной координаты r при истечении продуктов сгорания заведомо исключают возможность определения отношения Ve/V0 через hth ВРД с ДГ. В противоположность этому, в силу сохранения H удельный импульс Isp RDE с сужающимся центральным телом и цилиндрической "внешней" образующей сопла заметно уменьшится. То что это так, подтверждают низкие значения Isp, рассчитанные в [5] для четырех вариантов RDE, летящих с М0 = 5 в однородной стехиометрической смеси водорода и воздуха с параметрами атмосферы Земли на высоте 20 км. Эти значения Isp = 1990, 2350, 2300 и 2250 с "традиционно" для авторов [5] (см. [3]) завышены: определяя Isp, они почему-то не учитывают сопротивления наветренной части центрального тела воздухозаборника. Исправленные значения Isp близки к 1420, 1830, 1780 и 1720 с, однако даже завышенные величины Isp заметно меньше Isp ПВРД, который при тех же условиях по оценке авторов [3] равен 3500¸3900 с. Дополнительное возрастание энтропии в RDE также имеет место – в УВ, примыкающей к ДВ на границе свежей горючей смеси и продуктов сгорания. Правда, интенсивность этой УВ невелика.
Итак, утверждения о возможном увеличении тяговых характеристик ВРД на десятки процентов благодаря использованию ДГ необоснованны. Даже для дозвуковых и малых сверхзвуковых чисел Маха полета, на которых ВРД с МГ может по тяговым характеристикам уступать PDE, последние заведомо уступают ТРД с МГ. Поэтому преимущества ВРД с ДГ, если и возможно, то не по тяговым характеристикам, а по простоте конструкции (как при малых М0 по сравнению с ТРД) или по меньшей теплонапряженности тракта двигателя (напротив, при больших сверхзвуковых числах Маха М0 > 5 в сравнении c пульсирующим детонационно-дефлаграционным двигателем [6]).
Работа выполнена при поддержке РФФИ (проект 17-01-00126).
Рисунок: кривые Ve/V0 ПВРД (цикл Брайтона) и PDE, рассчитанные по идеальному кпд (PDEth) и по нестационарной модели
1. Зельдович Я.Б. К вопросу об энергетическом использовании детонационного горения // ЖТФ. 1940. Т. 10. Вып. 17. С. 1453-1461.
2. Heiser W.H., Pratt D.T. Thermodynamic Cycle Analysis of Pulse Detonation Engines // J. of Propulsion and Power. 2002. V. 18. No. 1. P. 68-76.
3. Егорян А.Д., Крайко А.Н., Пьянков К.С., Тишин А.П. О расчете характеристик импульсного детонационного двигателя и их сравнении с характеристиками ПВРД // Теплофизика и аэромеханика. 2016. Т. 23. № 2. С. 307-310.
4. Remeev N.Kh., Vlasenko V.V., Khakimov R.A. Analysis of operation process and possible performance of the supersonic ramjet-type pulse detonation engine // Pulse and continuous detonation propulsion / Eds. G. Roy, S. Frolov. Moskow: TORUS PRESS, 2006. P. 235-250.
5. Дубровский А.В., Иванов В.С., Зангиев А.Э., Фролов С.М. Трехмерное численное моделирование характеристик прямоточной воздушно-реактивной силовой установки с непрерывно-детонационной камерой сгорания в условиях сверхзвукового полета // Химическая физика. 2016. Т. 35. № 6. С. 49-63.
6. Крайко А.Н., Александров В.Ю., Александров В.Г. и др. Способ организации горения топлива и детонационно-дефлаграционный пульсирующий прямоточный воздушно-реактивный двигатель. 2016. Патент РФ № 2585328.
Александр Николаевич Крайко
Математический институт им. В.А. Стеклова РАН
Динамические явления в природе описываются дифференциальными уравнениями.
Мы сконцентрируемся на случае обыкновенных дифференциальных уравнений, хотя следы обсуждаемых эффектов и явлений можно найти и в уравнениях с частными производными. Вплоть до конца XIX века основные усилия математиков, механиков и физиков были направлены на получение явных решений уравнений динамики. Переворот в понимании подходов и приоритетов произвел А.Пуанкаре, который с одной стороны, объяснил, что в общей ситуации получение явных формул для решений дифференциальных уравнений дело безнадежное, а с другой стороны предложил ряд методов качественного исследования динамических систем. На этом пути была обнаружена типичность различных хаотических явлений сначала в гамильтоновой, а затем и в диссипативной динамике. Историю этих вопросов, а также математические определения понятия хаоса я и планирую обсудить в своей лекции.
Дмитрий Валерьевич Трещев