МГУ имени М.В. Ломоносова
Рассматриваются приближенные решения задачи о расширении области горячего ионизованного водорода, окружающего звезду с температурой порядка 10 000 К, в среду с заданным распределением плотности. Движение ионизованного газа считается изотермичным. Из-за сильного взаимодействия вещества и излучения вводится предположение о существовании баланса между поглощаемой и излучаемой средой энергией - в отличие от классической задачи о сильном взрыве, когда справедливо предположение о сохранении полной энергии движущегося газа.
Для данной задачи были получены аналитические решения в случае сферически симметричной задачи (с использованием метода Черного) и в случае осесимметричной задачи (с использованием метода Компанейца). Полученные в первом случае результаты хорошо согласуются с данными, поученными численным путем в работе [3].
Проводится анализ решения полученного при применении метода Компанейца для задачи о расширении области HII в неоднородном газе. Решалась осесимметричная, плоская задача. Для определения формы ударной волны было получено нелинейное уравнение в частных производных и найдено его аналитическое решение. Установлены отличия полученного решения от решения задачи о точечном взрыве в неоднородной атмосфере. При анализе данного решения были проведены оценки развития неустойчивости Рэлея-Тейлора, исходя из данных об ускорении ударной волны.
Приближенные решения задачи о расширении области HII представляют интерес, поскольку точные решения требуют решения уравнений радиационной газовой динамики, учитывающей радиационные процессы. Приближенные модели позволяют получать данные, которые хорошо согласуются с более сложными расчетами.
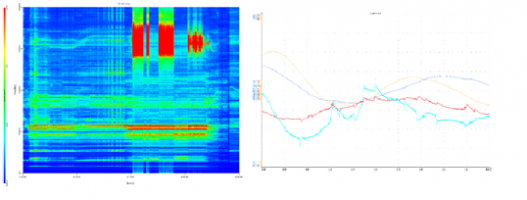
Результаты, полученные в ходе исследования расширения областей HII важны для изучения вопросов звездообразования. Например, на рис.1 изображена область HII, на периферии которой были обнаружены молодые звездные объекты. В ходе их исследования ставится следующий вопрос: существовали ли эти объекты до возникновения области HII или они образовались под влиянием расширения области HII.
1. А.С. Компанеец Точечный взрыв в неоднородной атмосфере Доклады Академии наук СССР. Том 130, №5, С. 1001-1003
2. К.В Краснобаев, Г.Ю. Котова, Р.Р. Тагирова Двумерные неустановившиеся движения фотоиспаряемых газовых оболочек Сборник "Проблемы современной механики: к 85-летию со дня рождения Г.Г. Черного. Изд-во Моск. ун-та изд-во "Омега-Л". Институт механики МГУ, 2008, С. 191-206
3. Zavagno A. et al. Triggered star formation on the borders of Galactic HII region RCW 120 Astronomy & Astrophysics -2007. - T. 472 -№3 -C. 835-846
4. Kim J.G., Kim W.T., Ostriker E.C. Disruption of Molecular Clouds by Expansion of Dusty HII Regions //The Astrophysical Journal. –2016. –T.819. –№.2. –С.137
5. Torii et al. Cloud-cloud collision as a trigger of the high-mass star formation: a molecular line study in RCW 120//The Astrophysical Journal. –2015. –T.806. –№.1. –С. 7.
Анна Сергеевна Гаврилова
ГНЦ ФГУП Центр Келдыша

Моделирование капиллярного распада струй вязких жидкостей является актуальной задачей для многих технических приложений. Одно из них – отвод низкопотенциального тепла в циклах космических энергетических установок нового поколения в процессе радиационного охлаждения специальным образом сформированного дисперсного потока, свободно распространяющегося в космическом пространстве [1]. Генерация капель осуществляется методом вынужденного капиллярного распада, а сбор остывшего рабочего тела – с помощью уловителя капель. К теплоносителю предъявляется требование низкой испаряемости. Все потенциально пригодные для использования в космосе рабочие тела имеют достаточно большую вязкость. Закономерности распада струй таких жидкостей при числе Онезорге, близком к единице, рассмотрены в работе [2], в которой получены зависимости размеров основных и сателлитных капель от волнового числа возмущения. Однако результаты экспериментальных исследований свидетельствуют о том, что капиллярный распад сильно вязких струй может сопровождаться образованием не только сателлитных капель, но и микросателлитов (или субсателлитов). При этом на одну основную каплю приходится несколько субсателлитов, масса которых может на несколько порядков отличаться от ее массы.
Ранее проводились исследования образования микросателлитов в процессе капиллярного распада струй маловязких жидкостей (например [3]). Однако из экспериментальных наблюдений известно, что процесс образования субсателлитов сложным образом зависит от числа Онезоге [4]. В представленной работе теоретически и экспериментально исследуется процесс образования микросателлитов при капиллярном распаде струй вязких жидкостей.
Микросателлиты образуются в области тонкого перешейка, соединяющего зародыши основной и сателлитной капель. При числе Онезорге, близком к единице, силы инерции пренебрежимо малы по сравнению с силами вязкости и поверхностного натяжения. Утончение струи происходит по автомодельной закономерности и слабо зависит от начальных условий. Эти закономерности рассмотрены в работе [5]. В представленной работе исследуется устойчивость автомодельных закономерностей вязкого утончения. Предложена теоретическая модель, позволяющая определить момент зарождения структуры зародышей микросателлитов на поверхности струи. Исследованы автомодельные закономерности отрыва зародыша микросателлита от струи. Объяснена фрактальная форма поверхности струи вблизи точки её разрыва. Проведено сравнение теоретически полученных результатов с экспериментом и численным расчётом.
Список использованных источников.
1. А.А. Коротеев, А.А. Сафронов, Н.И. Филатов. Влияние структуры капельной пелены на мощность бескаркасных космических излучателей и эффективность энергетических установок. Теплофизика высоких температур. 2016. Т. 54 № 5. С. 817–820. DOI: 10.1134/S0018151X16050175.
2. А.А. Сафронов. Особенности капиллярного распада струй жидкости при числах Онезорга больше единицы // Инженерно-физический журнал. 2017. Т. 90 №1. С. 176-185. DOI: 10.1007/s10891-017-1552-7.
3. Tjahjadi, M., Ottino, J. M., & Stone, H. A. (1992). Satellite and subsatellite formation in capillary breakup // Journal of Fluid Mechanics, V. 243, P. 297-317. 1992. DOI: 10.1017/S0022112092002738.
4. Campo D.L., Clasen C. The slow retraction method (SRM) for the determination of ultra-short relaxation times in capillary breakup extensional rheometry experiments // Journal of Non-Newtonian Fluid Mechanics. V. 165, Is. 23–24, December 2010, P. 1688–1699.
5. Jens Eggers. Stability of a viscous pinching thread // Physics of fluids, 24, 072103 (2012). http://dx.doi.org/10.1063/1.4732545.
Андрей Александрович Сафронов
ОКБ имени А. Люльки
В процессе сгорания топливовоздушной смеси в основных и форсажных камерах авиационных газотурбинных двигателях (ГТД) могут возникать различные, в том числе и автоколебательные процессы, сопровождающиеся изменениями скоростей и давлений потока. В зависимости от конструкции и назначения ГТД, данные процессы могут возникать на различных режимах как полета, так и работы летательного аппарата, а следовательно, приводить к ухудшению КПД двигателя и разрушению его конструкционных элементов. Для предупреждения и устранения таких процессов, необходима выработка диагностических признаков с целью разработки системы анализа и диагностирования опасных колебательных процессов, приводящих к уменьшению удельной тяги, ресурса двигателя и увеличению расхода топлива.
Алексей Игоревич Зубко
НИИ механики МГУ имени М.В. Ломоносова
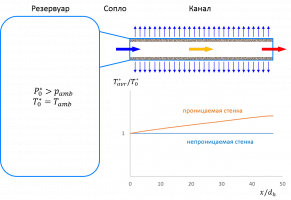
В работе рассмотрен новый вид безмашинного энергоразделения, основанный на отсосе «холодных» слоёв пограничного слоя при высокоскоростном течении газа в канале с проницаемыми стенками. На базе уравнений Навье-Стокса, дополненных уравнениями неразрывности, энергии, а также k-e модели турбулентности построена математическая модель устройства, реализующего данный вид энергоразделения. Задача рассматривались в осесимметричной постановке.
При использовании экспериментальных данных [1, 2] проведена валидация математической модели. На основе разработанной модели проведены параметрические исследования. Проанализирован широкий диапазон режимов течения: от непроницаемой стенки до асимптотического отсоса. Показано влияние начального числа Маха, а также молекулярного числа Прандтля на величину энергоразделения.
Работа выполнена при поддержке Российского научного фонда проект № 14-19-00699
Дмитрий Евгеньевич Хазов
ИПФ РАН
В настоящей работе предлагается методика пошаговой верификации результатов численных расчетов течений обтекания препятствия на основе их сравнения с результатами лабораторных экспериментов, осуществленных в рамках одного исследования.
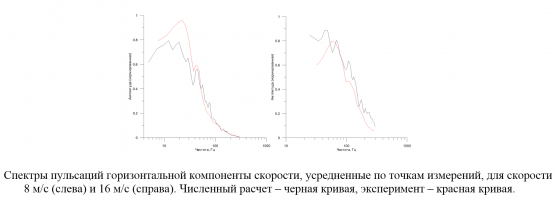
Лабораторные измерения проводились на замкнутой аэродинамической трубе ИПФ РАН, характеризующейся низким уровнем интенсивности турбулентности (~1%) на входе рабочего участка. В рабочий участок помещался объект препятствия (параллелепипед) для обтекания. Размеры объекта составляли 500х315х47 мм. Поперечный размер практически равен ширине рабочего участка, что обеспечивает двумерный характер обтекания в трубе. Тело устанавливалось на специальный столик, передняя кромка которого имела хорошо обтекаемый профиль, чтобы поток при подходе к препятствию был горизонтальный плоскопараллельный. Скорость воздушного потока в экспериментах составляла 8 м/с. Соответственно число Рейнольса рассчитанное по высоте препятствия равнялось 2,6*104.
Для измерений применялась схема PIV c непрерывной лазерной подсветкой и скоростной видеосъемкой [1]. В качестве модели турбулентности для численного решения задачи использоволся метод отсоединенных вихрей DES, который обеспечивает описание в пристеночной области (пограничном слое) при помощи модели напряжений Рейнольдса RANS, а в удаленной области (в свободной турбулентной струе) – при помощи метода крупных вихрей LES. Для решения нашей задачи в качестве RANS была выбрана модель переноса сдвиговых напряжений Ментера.
Сравнение результатов рассчетов с данными экспериментов осуществлялась в 2 этапа. Вначале сравнивались общие картины поля обтекания. Показано, что рассчет хорошо воспроизводит общую картину включая характерные размеры застойной области. На втором этапе сравнивались пульсационные характеристики воздушного потока обтекания - частотных спектров флуктуаций продольной компоненты скорости воздушного потока, полученных по данным PIV-измерений и численного моделирования. Анализ частотных характеристик представляет наибольший интерес с точки зрения многочисленных практических приложений, например, исследование вопроса генерации звука турбулентностью. Продемонстрировано, что форма рассчетных и экспериментальных спектров хорошо совпадают для эксперимента.
Исследования проведены при поддержке проекта РНФ №18-19-00473, проекта РФФИ №18-48-520023 р_а, гранта Президента СП-1740.2016.1.
1. Сергеев Д.А. Измерительный комплекс для исследования течений жидкости методом Particle Image Velocimetry (PIV) на основе твердотельного лазера с диодной накачкой // Приборы и техника эксперимента. 2009. № 3, С.138-144
Максим Игоревич Вдовин
Объединенный институт высоких температур Российской академии наук, Москва
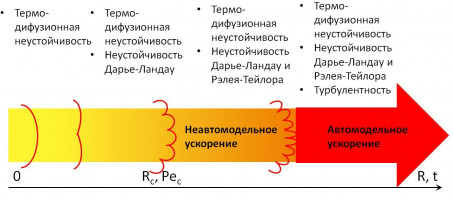
Расширяющиеся фронты химических реакции имеют отношение к процессам в двигателях с искровым зажиганием, к проблемам предотвращения взрывов, а также таких космических явлений, как термоядерное горение в сверхновых. При воспламенении горючей смеси газов в районе точки зажигания, возникает сферическое пламя. Сразу после зажигания пламя является гладким и сферическим. С увеличением размера фронт пламени деформируется и ускоряется. Ускорение фронта пламени является сложным процессом под действием теплового расширения, различных неустойчивостей–гидродинамических, термо-диффузионных, термо-акустических и турбулентности. Когда фронт пламени достигает критического значения Pe, его ускорение становится неавтомодельным, а затем автомодельным. Величина Pe представляет собой отношение радиуса фронта пламени к толщине фронта пламени. Л.Д. Ландау показал, что пламя становится неустойчивым к возмущениям всех длин волн при Re > 1. А.Г. Истратов и В.Б. Либрович показали, что пламя становится неустойчивым при Re > 103-104. Они учитывали влияние химической кинетики, диффузии и теплопроводности и показали, что эти процессы препятствуют развитию возмущений с малой длиной волны. На сегодняшний день существует множество методов моделирования ускорения пламени, как аналитических (фрактальный подход, анализ неустойчивостей, статистический турбулентный подход Колмогорова-Обухова…) так и численных (RANS, LES, DNS…).
Работа выполнена при поддержке Российского Научного Фонда, грант №14-50-00124
Виктор Владимирович Голуб
НИИ Механики МГУ имени М.В. Ломоносова
Исследования флаттера эластичных трубок при протекании через них жидкостей имеет приложение в различных областях. Например, изгибная неустойчивость может возникнуть в различных промышленных охладителях, включая охладители ядерных реакторов. Другим примером может служить потеря устойчивости и вибрации стенок сосудов в организме человека и животных [1]. Настоящая работа посвящена исследованию устойчивости течения степенной жидкости в упругих трубках конечной длины.
Трёхмерная система уравнений (уравнение Навье-Стокса для степенной жидкости и уравнение движения трубки), описывающая длинноволновые низкочастотные движения системы, сводится к одномерной системе уравнений путем интегрирования по поперечному сечению трубки.
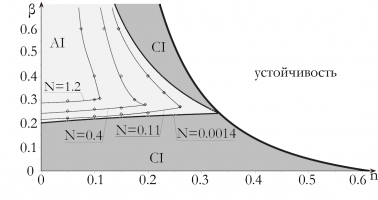
Для бесконечно длинной упругой трубки показано, что неустойчивость, при которой сохраняется осесимметричность движения трубки, возможна лишь при показателе степенного закона n<0.611. Однако, если неустойчивость будет конвективной, то она может не наблюдаться в реальности. Но если неустойчивость будет абсолютной, что возможно только при показателе степенного закона n<1/3, то локализованные возмущения растут во всей области [2].
Для трубок конечной длины без учёта продольного натяжения задача исследовалась аналитически. Найденная граница неустойчивости совпадает с границей абсолютной неустойчивости для бесконечно длинных трубок. При учёте продольного натяжения численно было показано, что область неустойчивости уменьшается при увеличении значения продольного натяжения N.
Анастасия Борисовна Подопросветова
Механико-математический факультет, БГУ, г. Минск
В работе исследовано плоское движение тонких несмешивающихся слоев вязких жидкостей на внешней поверхности горизонтально расположенного, вращающегося с постоянной угловой скоростью цилиндра в поле сил тяжести и инерции. Подобного рода течения можно использовать при нанесении двухслойных покрытий на цилиндрические поверхности. Используя условие постоянства потока в окружном направлении [1], в работах [2,3] решена задача определения вида поверхностей двух слоев в случае установившегося движения жидкостей как на внутренней, так и на внешней поверхности вращающейся цилиндрической оболочки.
В данном исследовании получена общая трехмерная постановка задачи движения двух несмешивающихся слоев вязких жидкостей в поле центробежных, поверхностных и гравитационных сил.
С помощью основных постулатов теории тонкого слоя [4] система уравнений, представляющая собой постановку двумерной нестационарной плоской задачи, была упрощена. В случае умеренного движения, пренебрегая инерционными членами уравнений Навье-Стокса, получены окружные и радиальные компоненты скорости, а также взаимосвязанная система уравнений эволюции наружного и внешнего слоев в гравитационном и поверхностном поле. Разработан и реализован численный метод ее исследования. Получены и проанализированы формы раздела слоев и свободной поверхности от длительного устойчивого состояния при медленном вращении до развития возмущений со временем и распада слоя при увеличении влияния центробежных сил.
Александр Игоревич Ермоленко
БГУ
В работе исследовано плоское движение тонких несмешивающихся слоев вязких жидкостей на внешней поверхности горизонтально расположенного, вращающегося с постоянной угловой скоростью цилиндра в поле сил тяжести и инерции. Подобного рода течения можно использовать при нанесении двухслойных покрытий на цилиндрические поверхности. Используя условие постоянства потока в окружном направлении [1], в работах [2,3] решена задача определения вида поверхностей двух слоев в случае установившегося движения жидкостей как на внутренней, так и на внешней поверхности вращающейся цилиндрической оболочки.
В данном исследовании получена общая трехмерная постановка задачи движения двух несмешивающихся слоев вязких жидкостей в поле центробежных, поверхностных и гравитационных сил.
С помощью основных постулатов теории тонкого слоя [4] система уравнений, представляющая собой постановку двумерной нестационарной плоской задачи, была упрощена. В случае умеренного движения, пренебрегая инерционными членами уравнений Навье-Стокса, получены окружные и радиальные компоненты скорости, а также взаимосвязанная система уравнений эволюции наружного и внешнего слоев в гравитационном и поверхностном поле. Разработан и реализован численный метод ее исследования. Получены и проанализированы формы раздела слоев и свободной поверхности от длительного устойчивого состояния при медленном вращении до развития возмущений со временем и распада слоя при увеличении влияния центробежных сил.
Анастасия Геннадьевна Макоед
Научно исследовательский институт механики МГУ им. М. В. Ломоносова
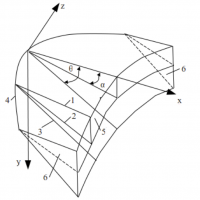
Поставлена и решена задача о форме волнолета максимального аэродинамического качества, построенного на плоской ударной волне и имеющего плоскость симметрии, при двух изопериметрических условиях: заданы удельный объем волнолета и коэффициент подъемной силы. Верхняя поверхность волнолета направлена по набегающему потоку и не возмущает его. Нижняя поверхность состоит из прямых, составляющих одинаковый угол α с невозмущенным потоком. Передняя кромка – кривая, расположенная в плоскости ударной волны, генерируемой нижней поверхностью и составляющей угол θ с направлением набегающего потока. Кроме давления в модели взаимодействия потока с поверхностями волнолета присутствует локальный коэффициент трения, изменяющийся, как на пластине, независимо вдоль каждой хорды от передней к задней кромке. Экстремаль – распределение длины хорды волнолета в плане по размаху находится с использованием метода локальных вариаций, адаптированного к вариационной задаче с двумя изопериметрическими условиями. Показано, что при нормированных специальным образом Су и Сх задача сводится к поиску минимума функционала Сх, зависящего от четырех параметров: α, М - числа Маха, С - тангенса угла, определяющего скос донного среза и m - параметра, характеризующего состояние пограничного слоя. Таким образом, в рамках применяемой модели экстремаль не зависит от числа Рейнольдса, а зависит только от состояния пограничного слоя. В качестве начального контура волнолета в плане принимался контур, состоящий из отрезков прямых, который, как показал анализ необходимых условий экстремума ни при каких сочетаниях определяющих параметров не является экстремалью. Определена форма оптимального волнолета при отсутствии и наличии ограничений на длину и размах волнолета, а также на тепловой поток к передней кромке при различных комбинациях определяющих параметров и состояниях пограничного слоя. Установлено, что оптимальный волнолет может содержать боковые шайбы, а криволинейный участок передней кромки как при отсутствии ограничения на тепловой поток, так и при его наличии содержит точку перегиба. Показано, что при уменьшении угла α аэродинамическое качество у оптимальных волнолетов увеличивается, а форма меняется незначительно. Угол скоса донного среза волнолета слабо влияет на K. Рост числа Маха при сохранении состояния пограничного слоя приводит к значительному изменению формы оптимального волнолёта.
Работа выполнена при частичной финансовой поддержке РФФИ (проект № 18-01-00182).
Сергей Сергеевич Страдомский
ФГУП "ЦАГИ"
В первой части лекции, которая носит обзорный характер, приведены результаты исследований гиперзвуковых течений вязкого газа начиная с середины XX века. Обсуждаются особенности течений для различных режимов вязко-невязкого взаимодействия, которые были установлены в экспериментальных работах Борового В.Я., Майкапара Г.И., Whitehead A.H., Hefner J.N., Rao D.M., Cross E.J. и др. Для режима сильного взаимодействия приведены автомодельные решения: Lees L.J. – Stewartson K. - обтекания полубесконечной пластины, Whalen R.J. - скользящей пластины и Ладыженского М.Д. - плоских треугольных крыльев. Далее обсуждаются вопросы, связанные с распространением возмущений против потока, которое впервые в 1970 году было установлено Нейландом В.Я. [1, 2]. Приведены результаты исследований Stewartson K. обтекания пластины с учетом решения уравнений для ударного слоя, а также решения Михайлова В.В., Нейланда В.Я., Дудина Г.Н. для обтекания треугольных крыльев на режиме сильного взаимодействия.
Во второй части лекции обсуждается вопрос о возможности образования пространственного течения на пластине конечной длины на режиме сильного взаимодействия. В предположении, что на задней кромке пластины задается дополнительное условие, которое является функцией от поперечной координаты и, учитывая вид первых членов разложения для функций течения в окрестности передней кромки [3], сформулированы и решены краевые задачи для определения следующих членов разложения. Впервые показано, что для функций течения p(x, z), δ(x, z), u(x, Y, z), ν(x, Y, z), H(x, Y, z) эти члены имеют порядок O( (pα(z)/p0)2 x2α), а для w(x, Y, z) - O( dpα(z)/dz (pα(z)/(p0)2) x2α+1), где α - собственное число и pα(z) - произвольный параметр. Установлено, что возникающее вторичное течение в сечениях пропорционально величине dpα(z)/dz.
На рисунке приведена зависимость du/dY на поверхности пластины, которая пропорциональна коэффициенту продольного трения, при температурном факторе Hw=1.5 и параметре pα(z)=0.2 cos(πz).
Рассмотрено также обтекание скользящей пластины. Установлено принципиальное отличие от предыдущего случая. Уравнение для w(x, Y, z) не отделяются от основной системы уравнений, а самое главное, третьи члены разложений имеют порядок O( (dpα(z)/dz) xα+1). Таким образом, при наличии угла скольжения, влияние третьего члена разложения на распространений возмущений существенно больше, чем при отсутствии скольжения. Установлено, что увеличение угла скольжения приводит к значительному уменьшению значений собственного числа.
Работа выполнена при финансовой поддержке РФФИ (проект № 18-01-00211).
1. Нейланд В.Я. Распространение возмущений вверх по течению при взаимодействии гиперзвукового потока с пограничным слоем // Изв. АН СССР. МЖГ. 1970. № 3. С. 40-49.
2. Нейланд В.Я., Боголепов В.В., Дудин Г.Н., Липатов И.И. Асимптотическая теория сверхзвуковых течений вязкого газа. – М.: Физматлит, 2003. – 456 с.
3. Дудин Г.Н., Нейланд В.Я. Об индуцировании трехмерных возмущений в пограничном слое при сильном взаимодействии с гиперзвуковым потоком // Изв. РАН. МЖГ. 2018. № 1. С. 89-96.
Георгий Николаевич Дудин
НИИ механики МГУ имени М.В. Ломоносова, Москва/ ООО "Тесис", Москва
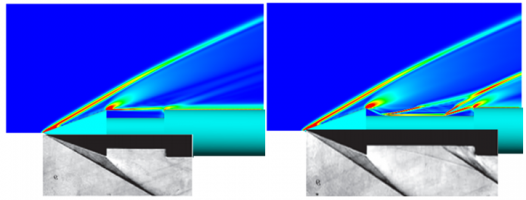
Представлены результаты экспериментального и численного исследования сверхзвукового обтекания осесимметричного тела с кольцевой каверной прямоугольного сечения.
В ходе экспериментов осуществлялось непрерывное изменение протяженности каверны при различных фиксированных углах атаки, а также непрерывное изменение угла атаки при фиксированной протяженности каверны. На основе данных визуализации и измерения давления изучена эволюция структуры обтекания каверны, включая режимы перестройки структуры на границах переходной области. В области исследованных диапазонов изменения угла атаки и относительной протяженности каверны определены границы переходной области, в которой возникают гистерезисные явления. Результаты весовых испытаний показали, что при наличии каверны сопротивление обтекаемого тела с замкнутым режимом течения в каверне может существенно превышать сопротивление аналогичного тела с открытым режимом течения. Экспериментально установлено, что в области гистерезиса возможно принудительное переключение с замкнутого режима обтекания каверны к открытому режиму [1].
Численное моделирование сверхзвукового осесимметричного обтекания тела с кольцевой каверной выполнено с использованием программного комплекса FlowVision. Проведено исследование сходимости задачи по расчетной сетке, определена оптимальная модель турбулентности. Выполнено сравнение с экспериментом. Исследовано влияние скорости изменения длины каверны на характер изменения течения. Проиллюстрирован механизм перестройки режимов течения в каверне при непрерывном изменении ее длины. Дана оценка протяженности области гистерезиса при сверхзвуковом обтекании тела с каверной. Показано, что внесение кратковременного возмущения в уже сформировавшееся течение позволяет изменить режим течения в каверне и тем самым увеличить или уменьшить сопротивление тела [2].
Исследования проводились в рамках госбюджетной темы АААА-А16-116021110201-2 НИИ механики МГУ (http://www.imec.msu.ru).
1.Гувернюк С. В., Зубков А. Ф., Симоненко М. М. Экспериментальное исследование сверхзвукового обтекания осесимметричной кольцевой каверны // Инженерно-физический журнал. 2016. Т. 89. № 3. С. 670–679.
2.Шишаева А. С., Симоненко М. М., Гувернюк С. В., Аксенов А. А.. Численное моделирование аэродинамического гистерезиса при сверхзвуковом обтекании осесимметричного тела с каверной в программном комплексе flowvision. // Физико-химическая кинетика в газовой динамике, 2017, Т. 18(1).
Анастасия Сергеевна Шишаева
ФИАН им. П.Н. Лебедева
На основании колмогоровского закона «4/5» [1, 2] получены аналитические соотношения для тройных двухточечных корреляций градиентов скорости и скорости в однородной изотропной несжимаемой турбулентности. Соответствующий тензор корреляции может быть выражен через скорость диссипации, корреляционную функцию продольного приращения скорости второго порядка и новую скалярную функцию. Некоторые компоненты тензора не зависят от новой функции. Полученные аналитические результаты согласуются с данными прямого численного моделирования стационарной изотропной турбулентности. Новая скалярная функция может быть с большой точностью аппроксимирована в инерционном диапазоне масштабов постоянным значением, зависящим только от скорости диссипации. Обсуждается значение полученных корреляторов в теории турбулентного транспорта [3, 4].
Исследование выполнено во ФГУП «Центральный аэрогидродинамический институт имени профессора Н.Е. Жуковского» за счет гранта Российского научного фонда (проект №17-11-01271)
1. Колмогоров А.Н. Рассеяние энергии при локально изотропной турбулентности // ДАН СССР, 1941, 32, 1, 19-21.
2. Ландау Л.Д., Лифшиц Е.М. Гидродинамика, М: Физматлит, 2006, 736 с.
3. Il'yn A. S., Sirota V. A., Zybin K. P. Statistical properties of the T-exponential of isotropically distributed random matrices // J. Stat. Phys., 2016, 7, 709.
4. Казанцев А.П. Об усилении магнитного поля проводящей житкостью // ЖЭТФ, 1967, 53, 5 (11), 1806-1813.
Алексей Викторович Копьев
Московский Авиационный Институт
Дальнейшее развитие ракетно-космической техники (РКТ) и, в частности, ее перспективного направления – гиперзвуковые летательные аппараты (ГЛА), тесно связано с созданием новых теплозащитных материалов (ТЗМ), способных защитить конструкцию от термохимической и механической эрозии. Для использования таких материалов в конструкции ГЛА необходимо знать спектр свойств, таких как: термостойкость, износостойкость, излучательные и каталитические свойства и др.
Каталитические и излучательные свойства материалов однозначно определяются компонентным составом, физико-химическими характеристиками, кристаллической структурой, пористостью, напряженным состоянием, глубиной пробега излучения и другими характеристиками. При этом следует иметь в виду, что в процессе интенсивного аэродинамического нагрева эти свойства изменяются.
Все сказанное выше, предполагает проведение комплексных экспериментально-теоретических исследований с целью изучения каталитических и излучательных свойств материалов. При этом такие исследования должны проводиться в условиях реального полета как для отдельных химических элементов, так и их композиций.
Каталитические свойства поверхности ТЗМ характеризуется константой скорости поверхностной рекомбинации, kw. Для экспериментального определения этого параметра, изготовляется калориметры охлаждаемого и неохлаждаемого типа, поверхность теплоприёмного элемента которого покрывается тонким слоем (5...10 мкм) термостойкого композиционного материала, подвергающегося исследованию.
Проведенный анализ показал, что из всех возможных технологий формирования на поверхности калориметра таких покрытий, наилучшей является – низкотемпературная газодинамическая технология.
В свою очередь, излучательные свойства поверхности ТЗМ характеризуются интегральной излучательной способностью, εw. Для её определения на стенде МАИ используется автоматизированная инфракрасная тепловизионная система серии М-9200 («MIKRON infrared, INS com.»,USA, рис.1) Температурное поле поверхности теплоприёмного элемента калориметра с тонким слоем теплозащитного покрытия, представлено на рисунке.
По результатам обработки эксперимента интегральная излучательная способность покрытия на поверхности теплоприёмного элемента калориметра определялась с использованием соотношения:
εw =( Тw,R / Тw, ист )^4, где Тw,R – радиационная температура при наличии подсветки от высокотемпературного набегающего потока, Тw, ист – истинная температура поверхности образца.
1. Никитин П.В., Шкуратенко А.А. Влияние каталитически активной поверхности на интенсивность конвективного теплообмена // Труды МАИ. 2016. №88.
2. Никитин П.В., Сотник Е.В. Катализ и излучение в системах тепловой защиты космических аппаратов // Янус-К, 2013-336с.
Анна Александровна Шкуратенко
Лаборатория вибрационной гидромеханики, Пермский государственный гуманитарно-педагогический университет, Пермь
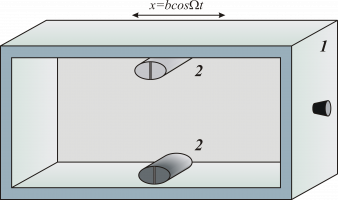
В работе представлены результаты экспериментального исследования вибрационной динамики твердых одиночных и множественных включений в форме эллиптических цилиндров в заполненном вязкой несжимаемой жидкостью прямоугольном контейнере, совершающем поступательные гармонические колебания.
Изучаются особенности поведения тел в зависимости от их относительного размера и плотности, количества тел в объеме жидкости, расстояния между телами и стенкой при различных значениях безразмерной амплитуды и частоты вибраций. Эксперименты проводятся в постановке, ранее описанной авторами в работе [1].
Для выяснения природы взаимодействия тел с границами полости и друг с другом, а также построения траекторий колебаний тел, проводится скоростная видеосъемка процесса с его последующей покадровой обработкой и анализом. С целью изучения структуры осредненных сдвиговых колебаний жидкости применяется P.I.V. методика.
При проведении исследования, наряду с осциллирующим движением тела, особое внимание уделено осредненным эффектам, возбуждаемым в результате колебаний тел в жидкости. В частности, изучению вибрационной подъемной силы, действующей на твердые эллиптические включения в непосредственной близости от твердых границ.
Эксперименты проводятся как с тяжелыми, так и с легкими эллиптическими цилиндрами. Особое внимание уделяется телам с плотностями, мало отличающимися от плотности жидкости, поскольку пробные эксперименты показали, что вибрационная подъемная сила, действующая на тела с относительной плотностью близкой к единице, имеет определенно другую природу, не связанную с инерционными колебаниями включения относительно жидкости.
Результаты исследований обобщаются на плоскости управляющих безразмерных параметров. Исследование проводится при варьировании в широком диапазоне безразмерной частоты и амплитуды вибраций полости. Особое внимание уделено предельному случаю низких безразмерных частот, когда размеры тел оказываются сравнимы с толщиной вязкого пограничного слоя Стокса.
Полученные результаты исследования могут найти активное применение в разработке эффективных методов управления твердыми включениями в вязкой жидкости.
Работа выполнена при финансовой поддержке Российского Научного Фонда (проект 18-71-00122).
1. V.D. Schipitsyn, V.G. Kozlov. Oscillatory and Steady Dynamics of a Cylindrical Body Near the Border of Vibrating Cavity Filled with Liquid // Microgravity Sci. Technol. (2018) 30: 103-112. DOI: https://doi.org/10.1007/s12217-017-9583-4
Виталий Дмитриевич Щипицын