БЕЗВОЛНОВОЕ СТЕКАНИЕ НЕНЬЮТОНОВСКОЙ ЖИДКОСТИ ПО ВЕРТИКАЛЬНОЙ ОСЦИЛЛИРУЮЩЕЙ ПЛОСКОСТИ
Автор: Регина Дамировна Вахитова
Соавторы: Могилевский Евгений Ильич, Николаев Егор Борисович
Организация: Механико-математический факультет МГУ имени М.В. Ломоносова, Москва
Толщина слоя со свободной поверхностью, стекающего по плоскости под действием силы тяжести определяется балансом массовой силы и трения на твердой поверхности. Для линейно-вязкой жидкости имеется точное решение уравнений Навье-Стокса, которое предсказывает, что расход жидкости пропорционален третьей степени толщины. При течении неньютоновской жидкости эта зависимость определяется реологическим законом, в частности, для степенной жидкости (эффективная вязкость является степенной функцией скорости сдвига) показатель степени зависит от показателя вязкости и расход пропорционален большей степени толщины для псевдопластических жидкостей и меньшей для дилатантных. В случае нелинейного закона зависимости вязкости от скорости сдвига колебания плоскости приводят к локальному изменению трения и существенному изменению расхода, причем его среднее значение по периоду также изменяется.
Изучается зависимость среднего расхода стекания неньютоновской жидкости по наклонной плоскости от параметров колебаний. Периодическое решение нелинейного уравнения в частных производных параболического типа разыскивается с помощью различных подходов. Рассмотрены асимптотические случаи: медленные колебания, период которых много больше времени вязкой релаксации, вызывающие квазистационарное течение; быстрые колебания, которые приводят к образованию тонкого осциллирующего подслоя; слабая зависимость вязкости от скорости сдвига. В первых двух случаях удается аналитически найти вид зависимости расхода от параметров колебаний. Для слабо неньютоновских жидкостей задача сводится к линейному неоднородному уравнению, периодическое решение которого находятся методом Фурье.
Для произвольного реологического закона и произвольных параметров колебаний решается нестационарная задача, периодическое решение устанавливается за достаточно большое время.
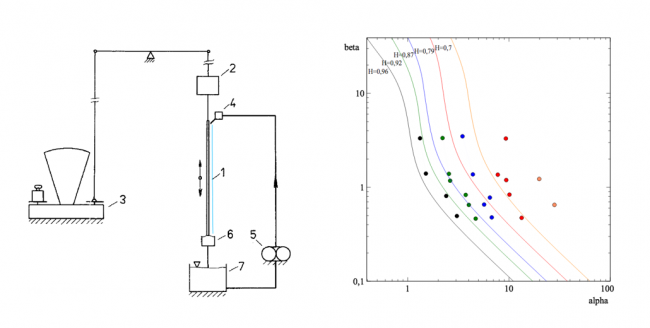
Результаты расчетов сравниваются с опубликованными экспериментальными данными. По осям отложены безразмерная амплитуда скорости плоскости и частота колебаний. Обнаружены значительные расхождения при малых амплитудах и частотах колебаний, различия, вероятно, связаны с недостаточно точно выбранной реологической моделью.
Работа выполнена при поддержке Совета по грантам при Президенте РФ (проект МК -1798.2017.1)
