К ЧИСЛЕННОМУ ИНТЕГРИРОВАНИЮ УРАВНЕНИЙ НЕЛИНЕЙНОЙ АКУСТИКИ ПРИМЕНИТЕЛЬНО К ЗАДАЧЕ О ЗВУКОВОМ УДАРЕ
Автор: Харис Фаритович Валиев
Соавторы: А.Н. Крайко, К.С. Пьянков, Н.И. Тилляева
Организация: ЦИАМ
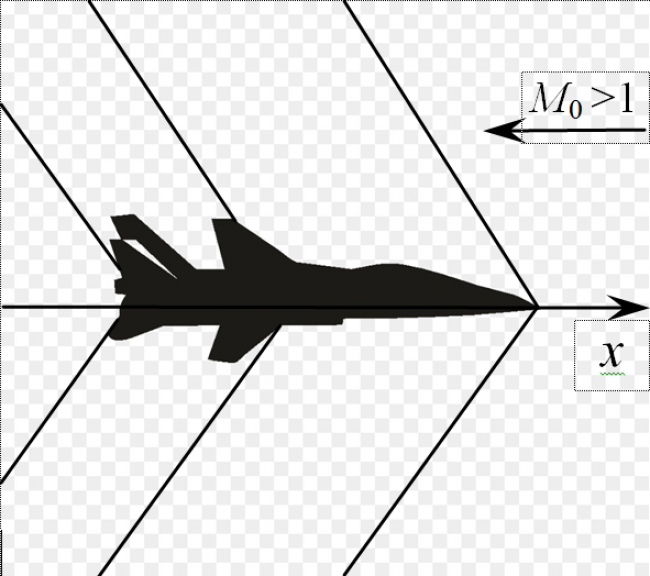
Рассматриваются возможности численных и аналитических инструментов описания звукового удара – следствия сверхзвуковой скорости летательных аппаратов. Несмотря на стремительный рост быстродействия и памяти компьютеров и прогресс вычислительной газовой динамики, возможности численного решения уравнений течения ограничены расчетом структур, возмущения параметров в которых не очень малы (больше 10–2-10–3 их значений в невозмущенном потоке). В результате, при изучении звукового удара численный расчет обтекания летательных аппаратов ограничен расстояниями в несколько их длин при удалении земной поверхности на сотни таких длин. На бόльших расстояниях используется численно-аналитический аппарат со сложными формулами – решениями линеаризованных уравнений Эйлера и главными нелинейными поправками к ним. Важный результат таких расчетов – осесимметричная асимптотика, согласно которой вдали от летательного аппарата структуры, примыкающие к головной ударной волне, затухают, как осесимметричные, свои на разных меридиональных плоскостях. В докладе с учётом опыта расчетов ударно-волновых структур перед сверхзвуковыми решетками [1] показана возможность быстрого и точного расчета ударно-волновых структур звукового удара при численном решении уравнений Эйлера без ограничений на расстояния и малую интенсивность затухающих ударных волн. Ключевую роль при этом играет адаптация разностной сетки к особенностям ударно-волновой структуры звукового удара. В известных авторам программах расчета звукового удара в приближении уравнений невязкого газа в лучшем случае удается обнаружить лишь движение в требуемом направлении (см., например, [2, 3]). Правильно адаптированных сеток нет нигде. Наконец, расчет эволюции структуры звукового удара в осесимметричном приближении с удаления в 15-20 длин летательного аппарата до земной поверхности сведен к мгновенному (доли секунды на персональном компьютере) решению задачи Коши для обыкновенных дифференциальных уравнений.
