Компактная разностная схема для эллиптических уравнений с разрывным коэффициентом. Линия скачка коэффициента с изломом
Автор: Дмитрий Андреевич Шадрин
Соавторы: В.А. Гордин
Организация: НИУ ВШЭ, Гидрометцентр РФ.
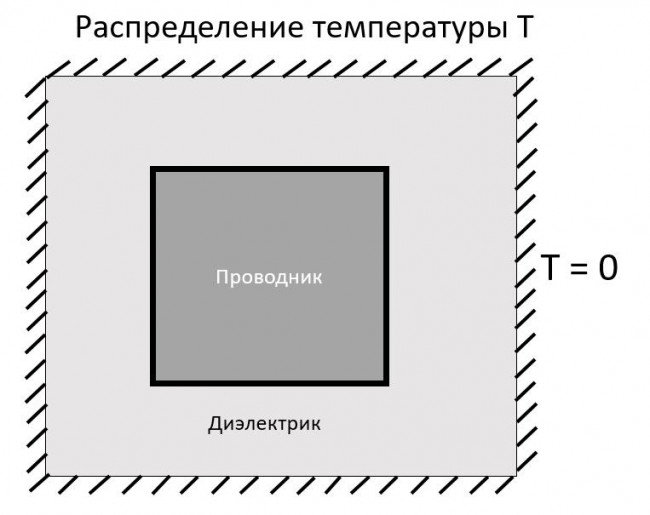
Рис. 1. Схема области вычислений Ω, разделенной на однородные подобласти Ω1, Ω2, линия скачка Г обозначена жирной линией.
Разработана компактная разностная схема 4-го порядка точности для решения 2-мерных краевых задач для уравнений Пуассона (1) и Гельмгольца (2), которые имеют множество приложений в технике и физике (в т.ч. геофизике [1]). Как правило, коэффициент θ - кусочно-непрерывная функция, она имеет скачок на линии Г, которая содержит изломы. В данном случае (см. Рисунок)
div(θ(x,y)grad(u(x,y))= f(x,y), (1)
div(θ(x,y)grad(u(x,y)) + ρU(x,y)= f(x,y), (2)
На внешней границе вычислительной области для решения u ставятся граничные условия Неймана или Дирихле. На линии стыка Г - условия Кирхгофа (3).
[u] = 0 (3а),
[∂nu] = 0 (3b).
Здесь [] – осцилляции функции на Г, ∂n - производная вдоль нормали к Г.
Задача (1,3) симулирует распределение тепла (или электростатического потенциала (2, 3)) для области из двух сред, например, проводника прямоугольного сечения, окруженного слоем диэлектрика.
Численные эксперименты подтверждаю 4-й порядок компактной схемы при большом скачке коэффициента θ (примерно в 10000 раз), данные порядок точности не достигался в других работах (см. [2]). Особая сложность компактной аппроксимации состоит в подборе шаблонов и тестовых функций (см. [3]) для аппроксимации дифференциальной задачи около углов Г. В точках излома Г для аппроксимации было использовано разложение решения u в ряд по обобщенным собственным функциям дифференциального оператора из уравнения (1), данные функции брались в качестве тестовых. В точках около углов использовался смешанный набор из обобщенных собственных функций и мономов.
Работа подготовлена в ходе проведения исследования (№ 20-04-021) в рамках Программы «Научный фонд Национального исследовательского университета „Высшая школа экономики“ (НИУ ВШЭ)» в 2020 — 2021 гг. и в рамках государственной поддержки ведущих университетов Российской Федерации «5-100».
[1] M.Schneider, D.Gläser, B.Flemisch, R. Helmig, Comparison of finite-volume schemes for diffusion problems, Oil Gas Sci. Technol. Rev. IFP
Energ. Nouvelles 73 (2018) 82, http://dx.doi.org/10.2516/ogst/2018064.
[2] Raphaele Herbin, Florence Hubert. Benchmark on Discretization Schemes for Anisotropic Diffusion
Problems on General Grids. Finite volumes for complex applications V, Jun 2008, France. pp.659–692.
ffhal-00429843f
[3] А. А. Самарский Е. С. Николаев, Методы решения сеточных уравнений. Главная редакция физико-математической литературы изд-ва Наука*,М., (1978)
