Многократное маховское отражение при дифракции ударной волны на клине
Автор: Андрей Николаевич Максимов
Организация: МГУ им. М.В. Ломоносова
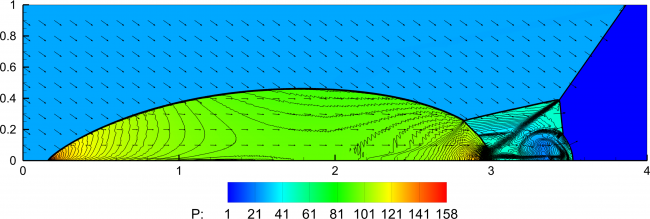
Проблема дифракции ударной волны на клине, впервые описанная еще в XIX веке Махом, по сей день является не до конца изученной, несмотря на многочисленные экспериментальные, численные и теоретические исследования, проводимые в этой области. Самая полная на данный момент классификация различных автомодельных конфигураций регулярного и маховского отражения приведена в [1]. В зависимости от определяющих параметров задачи (числа Маха ударной волны, показателя адиабаты газа и угла клина) в расчетах и экспериментах [1] наблюдались различные конфигурации с ординарным, двойным и даже тройным маховским отражением.
В настоящей работе исследованы конфигурации, характеризующиеся отрицательным углом наклона отраженного скачка [2] (скачок расположен ниже траектории движения тройной точки). Численные расчеты выполнены с использованием TVD модификации явной схемы МакКормака [3]. Расчетная область повернута так, что горизонтальная ось направлена вдоль образующей клина, а падающая ударная волна наклонена на угол клина (Рис. 1). В начальный момент ударная волна проходит через вершину клина, и параметры течения определяются соотношениями Рэнкина-Гюгонио на скачке. В процессе расчета поддерживаются граничные условия на левой и верхней границе, соответствующие движению ударной волны с известным числом Маха.
Обнаружен новый автомодельный режим многократного (четырехкратного) маховского отражения, характеризующийся ветвлением ударно-волновых конфигураций (Рис. 1). Для умеренных значений числа Маха режим реализуется в газах с показателем адиабаты близким к единице. Выполнение условия автомодельности проверялось сравнением распределений параметров в различные моменты времени. Проведено исследование перехода от нового режима отражения к регулярному отражению при изменении угла клина. Определены границы существования конфигураций многократного отражения при изменении показателя адиабаты газа.
Работа выполнена под руководством П.Ю. Георгиевского при частичной финансовой поддержке РФФИ (проект 18-01-00793-а).
