О ВОЗМОЖНЫХ ПОПРАВКАХ К УРАВНЕНИЮ НАВЬЕ-СТОКСА ПО ЧИСЛУ КНУДСЕНА

Автор: Аунг Зо

Соавторы: С.О. Гладков

Организация: Московский авиационный институт (национальный исследовательский университет) (МАИ)

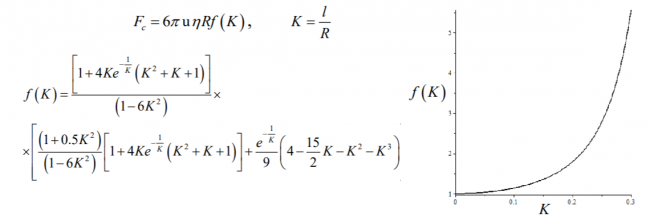
   В настоящем сообщении речь пойдет о вычислении поправок к уравнению Навье – Стокса в виде дополнительных слагаемых по длине свободного пробега молекул.

   Формально это означает, что малым параметром задачи является число Кнудсена, стандартно определяемого как , где  длина свободного пробега молекул жидкости или газа,  линейный размер тела.

    Важность нахождения этих поправок обусловлена интересом научной общественности к исследованию различных свойств наночастиц, в том числе и гидродинамических. Он связан с тем, что в последнее время довольно модными объектами исследования стали частицы, размер которых колеблется в диапазоне . Если речь идет о подобного рода линейных размерах, то классическими формулами, например, формулой Стокса для шара, воспользоваться довольно проблематично, поскольку в этом случае длина свободного молекул оказывается сравнимой с линейным размером тела.

   Все вычисления будут проведены с помощью хорошо проверенного, как теорией, так и практикой, метода классического кинетического уравнения Больцмана (см., к примеру, [1] – [3]). Благодаря этому подходу мы дадим подробный вывод уравнения Навье – Стокса с учетом всех дополнительных слагаемых с точностью до членов порядка  по времени релаксации , где  импульс молекулы. Проведенные вычисления позволяют получить ответ на поставленный вопрос, и выявить все дополнительные дивергентные слагаемые к правой части уравнения Навье Стокса. Одним из них будет бигармонический оператор, входящий в уравнение со знаком минус. Как это будет строго аналитически показано, наличие этого слагаемого дает возможность вычислить соответствующие поправки по числу Кнудсена  к силе Стокса (см. также [4] – [6]).

1. S.O. Gladkov. The theory of thermal conductivity and hydrodynamics of Maxwell gas, which is under the influence of an external sound wave. Solid State Communications. 1995. V. 94. N9. PP.789 – 791.

2. Е.М. Лифшиц, Л.П. Питаевский. Физическая кинетика. Т. 10. М.: Наука. 1979. 528 с. 

3. П. Резибуа, М. Де Лернер. Классическая кинетическая теория жидкостей и газов. М.: Мир. 1980. 423 с.

4. С.О. Гладков. О доказательстве единственности гидродинамического решения Стокса. Известия вузов. Физика. 2018. Т. 61. В. 6. СС. 103 – 105. 

5. С.О. Гладков. О конвективном движении газа в цилиндрическом объеме. Письма в ЖТФ. 2005. Т. 31. В. 12. СС. 71 – 75.

6. С.О. Гладков. К вопросу о вычислении времени остановки вращающегося в вязком континууме цилиндрического тела и времени увлечения соосного с ним внешнего цилиндра. ЖТФ. 2018. Т. 59. В. 3. СС. 377 – 341.