Расчет оболочки вращения с использованием теории течения на основе МКЭ в смешанной формулировке

Автор: Виталий Рябуха

Соавторы: Гуреева Н.А.

Организация: ФГБОУ ВО «Финансовый университет при Правительстве РФ», г.Москва; ФГБОУ ВО «Волгоградский государственный аграрный университет», г.Волгоград

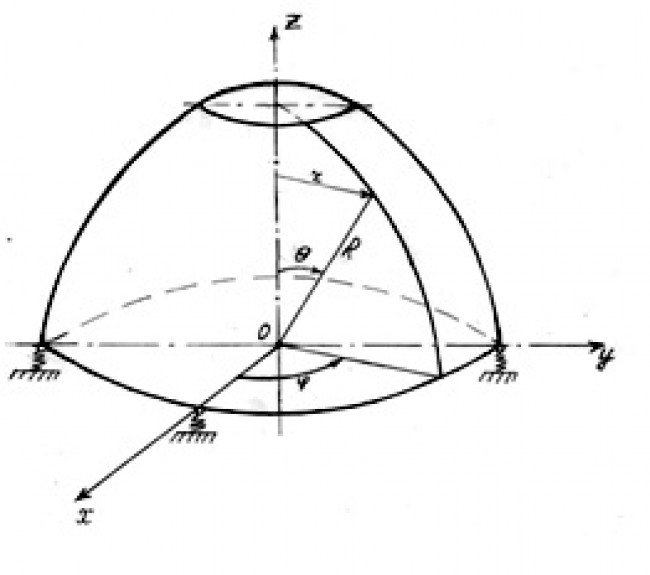
В расчете произвольно нагруженной оболочки вращения (Рис.1) при шаговом процессе нагружения используется метод конечных элементов (МКЭ) в смешанной формулировке при учете физической нелинейности на основе теории пластического течения.

В качестве конечного элемента выбрана в глобальной системе координат призма с треугольным основанием. Узловыми неизвестными приняты приращения перемещений и приращения напряжений. Для выполнения численного интегрирования по объему конечного элемента он отображается на локальную призму с основанием в форме равнобедренного треугольника (координаты ) с координатой  по высоте, изменение которой выражается неравенством .

Для выражения глобальных координат через их узловые значения использовались линейные функции от координат  [1] и линейные функции от координаты  [1]. Такие функции использовались и для аппроксимации как приращений перемещений внутренней точки конечного элемента через их узловые значения, так и для приращений напряжений.

Определяющие уравнения на шаге нагружения принимались на основе теории пластического течения. Полные приращения деформаций являются суммой деформаций упругих и пластических [2]. Приращения упругих деформаций получались на основе закона Гука. Приращения пластических деформаций определялись на основе гипотезы о пропорциональности приращений пластических деформаций компонентам девиатора полных напряжений. Коэффициент пропорциональности при этом является функцией отношения приращения интенсивности напряжений к интенсивности напряжений. Приращения интенсивности напряжений представлялись в общем виде зависимостью от приращений напряжений. После чего в матричном виде формировались соотношения между полными приращениями деформаций и приращениями  напряжений.

Матрица напряженно-деформированного состояния конечного элемента на шаге нагружения формируется с использованием функционала, основанного на равенстве возможных и действительных работ внешних и внутренних сил с заменой в нем действительной работы внутренних сил разностью полной работы приращений напряжений и их дополнительной работы [3].

После подстановки в функционал определяющих уравнений в матричном виде и аппроксимирующих выражений искомых величин (приращений перемещений и приращений напряжений) выполняется его минимизация по узловым неизвестным, в результате чего получается матрица напряженно-деформированного состояния конечного элемента на шаге напряжения.

Исследование выполнено при финансовой поддержке РФФИ и Администрации Волгоградской области в рамках научного проекта № 19-41-340004 р_а.