Влияние формы неровностей на характеристики периодического дискретного контакта

Автор: Анастасия Александровна Яковенко

Организация: Институт проблем механики им. А.Ю. Ишлинского РАН

Учет шероховатости взаимодействующих тел приводит к необходимости рассмотрения задач дискретного контакта. Шероховатость представляет собой совокупность неровностей различной формы и размеров, расстояние между которыми много меньше характерной длины макротела. Шероховатость образует микрорельеф, который может иметь случайный (статистический) или регулярный характер. В данной работе рассмотрен регулярный микрорельеф, который моделируется периодической системой одинаковых инденторов.

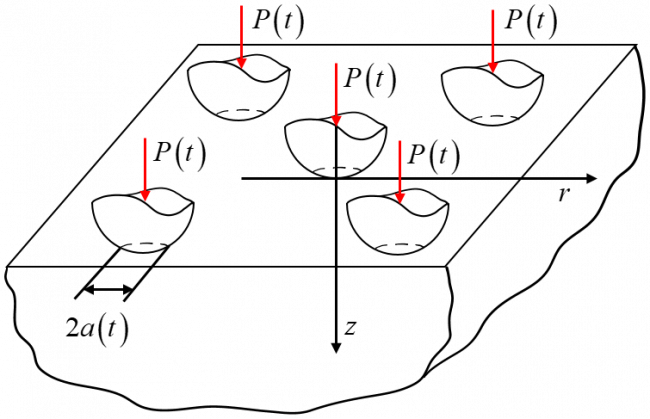
Исследовано взаимодействие с вязкоупругим полупространством периодической одноуровневой системы жестких инденторов (рис.1), форма поверхности которых описывается степенной функцией, а именно произведением константы на радиальную координату в степени 2n (n - натуральное число). К каждому индентору в нелевой момент времени прикладываетс постоянная заданная нагрузка. Плотность расположения инденторов определяется средним количеством неровностей на единице площади N. Регулярность пространственного расположения неровностей позволяет ввести величину номинального давления (как произведение нагрузки на N).

Для решения задачи использовался метод локализации [1], согласно которому в рассмотрение берется лишь заданное количество неровностей, ближайших к рассматриваемому, а действие остальных заменяется распределенным по полупространству вне круга радиуса A номинальным давлением. В данной работе исследовался простейший случай, когда реальное распределение контактных давлений учитывается только под поверхностью рассматриваемого индентора. Для описания поведения вязкоупругого полупространства используются интегральные соотношения с одной функцией релаксации  (или соответствующей функцией ползучести), то есть считается, что коэффициент Пуассона постоянен. Показано, что вязкоупругая задача сводится к аналогичной задаче в упругой постановке. Исследована модель Максвелла и модель стандартного вязкоупругого тела.

Получены зависимости от времени следующих контактных характеристик: распределение контактного давления на единичном пятне контакта, радиус единичного пятна контакта и функция дополнительного смещения. Исследовано влияние на эти характеристики формы неровностей и плотности их расположения. Для случая n=1 результаты представлены в работе [2]. Показано также, как с помощью полученных результатов можно перейти к задаче на макроуровне, то есть исследования взаимодействия тел на макроуровне с учетом микрорельефа контактных поверхностей [3].  

Работа выполнена при поддержке РФФИ (грант № 20-01-00400).

1.Горячева И.И. Механика фрикционного взаимодействия. М.: Наука. 2001. 478 с.

2.Yakovenko A., Goryacheva I. The Periodic Contact Problem for Spherical Indenters and Viscoelastic Half-Space // Tribology International. 2021.

3.Goryacheva I.G. Mechanics of discrete contact // Tribology International, 39. 2006. Pр. 381-386.