ЗАДАЧА КОШИ ДЛЯ КОЛЕБЛЮЩЕГОСЯ ЦИЛИНДРА В ЦИРКУЛЯЦИОННОМ ПОТОКЕ И ИНТЕНСИФИКАЦИЯ ЗАВИХРЕННОСТИ В КРИТИЧЕСКОМ СЛОЕ
Автор: Михаил Александрович Юдин
Соавторы: Копьев Виктор Феликсович, Чернышев Сергей Анатольевич
Организация: Центральный аэрогидродинамический институт имени профессора Н.Е. Жуковского
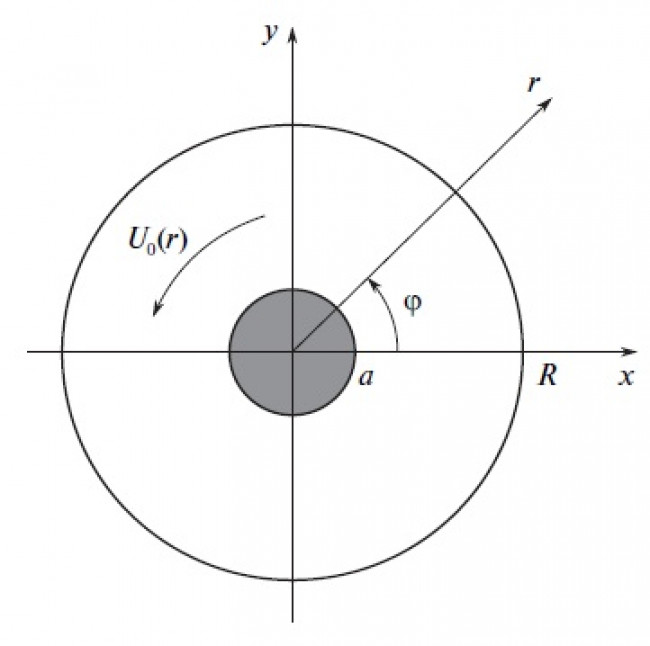
Данная работа является продолжением работ, посвященных неустойчивости цилиндра в циркуляционном потоке жидкости [1,2] и нацелена на более подробное изучение сдвиговой неустойчивости, возникающей в задаче. Сдвиговая неустойчивость представляет большой интерес, так как является причиной неустойчивости трехмерных вихрей, и по-видимому отвечает за турбулизацию вихревого кольца при больших числах Рейнольдса [3]. Исследование данной неустойчивости в трехмерных задачах представляет большие трудности. Задача о неустойчивости цилиндра радиуса a при обтекании его потоком жидкости с угловой скоростью U0(r), ограниченным стенками внешнего кожуха радиуса R (рис.1), представляется наиболее простой, в которой может быть выявлена сдвиговая неустойчивость, связанная с потоком энергии из критического слоя к колебаниям системы.
Ранее была решена задача о собственных колебаниях цилиндра в циркуляционном потоке жидкости [2]. Однако, собственные колебания не определяют полностью динамику этой системы, поскольку ее спектр содержит не только дискретную, но и непрерывную часть. В частности, представляет интерес начальная задача, решение которой является суперпозицией возмущений всего спектра.
Для исследования течения в области между цилиндрами используется аппарат поля смещения ε(r,t). Возмущение поля завихренности пропорционально радиальной компоненте поля смещения . Решение задачи Коши для поля смещения в кольце a<r<R выписывается в общем виде с помощью преобразования Лапласа. Для частных случаев (случай малой завихренности), интегралы могут быть вычислены точно. Таким образом, может быть построена зависимость завихренности от времени во всем течении.
Показано, что установление колебательного режима сопровождается перестройкой течения вблизи критического слоя. При этом поле смещения жидких частиц имеет сильно изрезанный характер и нарастающую по времени амплитуду.
Полученное решение для поля завихренности позволяет рассчитать поток энергии. Расчет потока энергии может быть проведен не только в случае малой монотонной завихренности, но и в точной постановке для течения с завихренностью обратно пропорциональной расстоянию до оси цилиндра.
Работа выполнена при поддержке Российского фонда фундаментальных исследований (грант №16-01-00746).
