Московский Государственный Университет им. М.В. Ломоносова
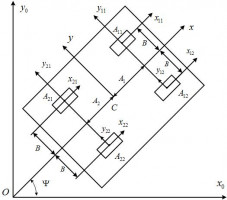
Рассматривается динамика корпуса двухосного четырехколесного аппарата (автомобиля, робота и т.д.) при попадании колес ведущей оси на «микст» – участок опорной плоскости с различными коэффициентами трения для колес одной оси. Для автомобиля такая ситуация возможна при въезде на обледенелую обочину, в лужу масла и т.п. Ранее в [1,2] было показано, что после завершения быстрого переходного процесса выравнивания контактных сил корпус аппарата получает импульс угловой скорости, способный привести к заносу. В зависимости от условий движения аппарата рассматриваются разные модели сил взаимодействия его колес с опорной плоскостью. Для описания динамики колес аппарата без потери сцепления с опорной плоскостью используются модель непроскальзывания и модель увода в продольном и поперечном направлениях, для описания скольжения колес – модель трения кулона и модель поликомпонентного сухого трения. Математические модели динамики аппарата формируются с использованием методов разделения быстрых и медленных движений, основанных на подходах фракционного анализа и теории сингулярных возмущений [3]. Возможность их применения связана с сильным разнесением постоянных времени движения аппарата на начальной стадии заноса [1–4]. Получены оценки импульсов угловой скорости, и показано, что моменты верчения колес слабо влияют на эти оценки, но важны при исследовании динамики корпуса аппарата на «миксте» после воздействия импульса угловой скорости. Описано развитие заноса, определяемого более медленной динамикой корпуса аппарата, для перечисленных случаев движения с уводом и со скольжением колес.
Благодарности. Данная работа была поддержана Фондом развития теоретической физики и математики «БАЗИС», грант 19-8-2-29-1.
1.Новожилов И.В., Павлов И.С., Фрольцов В.А. О поведении автомобиля на «миксте» // Механика твердого тела. 2001. № 3. C. 61–67.
2.Влахова А.В., Новодерова А.П. Занос колесного аппарата на «миксте» // Вестник Московского университета. Серия 1: Математика. Механика, издательство Изд-во Моск. ун-та (М.). №5.
3.Влахова А.В. Математические модели движения колесных аппаратов. М.-Ижевск: АНО «Ижевский институт компьютерных исследований», 2014. 148 с.
4.Влахова А.В., Новодерова А.П. Моделирование заноса аппарата с повернутыми передними колесами // Изв. РАН. МТТ. 2019. № 1. с.23-49.
Анна Павловна Новодерова
Механико-математический факультет МГУ имени М.В. Ломоносова, Москва; НИИ механики МГУ имени М.В. Ломоносова, Москва
В работах [1-3] предложен феноменологический метод описания аэродинамических сил и моментов, действующих на ротор Савониуса в воздушном потоке. Данный метод позволяет описать аэродинамическое воздействие потока на ротор в виде функциональной зависимости сил и моментов от мгновенных значений обобщенных координат и скоростей, а также параметров систем, содержащих в своем составе ротор Савониуса. Как следствие такой подход дает возможность исследовать сложные механические системы, используя малопараметрические модели.
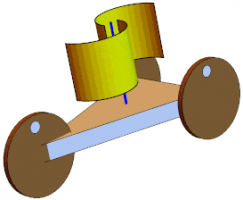
На основе упомянутого метода в данной работе исследуется динамика механической и электромеханической систем, в состав которых входит рассматриваемый тип ротора. А именно, построены математические модели ветроэнергетической установки на базе ротора Савониуса и ветродвижителя с ротором Савониуса. В первом случае энергия ветра преобразуется в электроэнергию, во втором – в полезную работу – движение ветромобиля, а ротор всегда выступает в качестве ветроприемного элемента. Описаны характеристики установившихся режимов движения и переходных процессов в зависимости от параметров и начальных условий.
Данное исследование в отличие от работы [4] учитывает зависимость аэродинамического воздействия на ротор и от угловой скорости вращения, и от угла поворота относительно набегающего потока. Обсуждается, какие свойства динамики изучаемых объектов можно уловить, используя не только усредненное значение момента на обороте, как это принято делать в таких случаях.
1. Мастерова А.А. Моделирование динамики малогабаритной ветроэнергетической установки на базе ротора Савониуса/ Труды конференции-конкурса молодых ученых. 13-17 октября 2017 г. / М.: Издательство Московского университета, 2018. – 140-147 с.
2. Мастерова А.А. Моделирование динамики колесной тележки, приводимой в движение с помощью ротора Савониуса/ Труды конференции-конкурса молодых ученых. 15-17 октября 2018 г. / М.: Издательство Московского университета – 98-105 с.
3. Мастерова А.А. Эмпирический подход к описанию воздействия потока на ротор Савониуса/ Тезисы конференции-конкурса молодых ученых Научно-исследовательского института механики МГУ имени М.В. Ломоносова 21-25 октября 2019 г. – с. 21.
4. Мастерова А.А. Динамика колесной тележки с ротором Савониуса / Всероссийская конференция молодых ученых-механиков YSM-2018. Тезисы докладов (4 − 14 сентября 2018 г., Сочи, «Буревестник» МГУ) / M.: Издательство Московского университета, 2018. – 116-116 с.
Анна Андреевна Мастерова
Самарский национальный исследовательский университет имени академика С.П. Королева
Проблема засорения околоземного космического пространства – одна из важнейших проблем, стоящих перед человечеством сегодня. В 1987 году американский астрофизик Дональд Кесслер рассмотрел возможные последствия неконтролируемого увеличения количества искусственных объектов на орбите. Рассмотренный им процесс, названный эффектом Кесслера, показал возможность лавинообразного роста космического мусора, который может быть инициирован столкновением всего двух крупных объектов [1]. Количество объектов космического мусора на орбите нашей планеты по данным на 2010 год составляет около 16 тыс. [2] и это число с каждым годом растет, а значит растет и вероятность сценария, предложенного Кесслером.
В работе рассматривается процесс увода крупногабаритного космического мусора посредством буксировки на гибкой сцепке и влияние на этот процесс выбора точки закрепления троса. Буксир моделируется как материальная точка, космический мусор – как твердое тело, трос рассматривается как упругий, невесомый стержень, ориентация тела определяется углом φ между осями систем координат [3].
Рассмотрено движение в бессиловом и центральном ньтоновском гравитационном полях в случаях плоского и пространственного движения. Проведена серия численных экспериментов.
1.Kessler D.J., Cour-Palais B.G. Collision frequency of artificial satellites: the creation of a debris belt // Journal of geophysical research, 1978, vol. 83, pp. 2637 - 2646.
2.Wood A. Gravity by Alfonso Cuarón // Science Fiction Film and Television, 2014, vol. 7, no. 3, pp. 441 - 444.
3.Файзуллин Л. Ф. Управление связкой буксир-космический мусор на этапе буксировки [Текст]/ Л. Ф. Файзуллин // Королевские чтения. 2019. Т. 1. С. 71 - 72
Ленар Фаязович Файзуллин
Механико-математический факультет МГУ имени М.В. Ломоносова
В работе рассматривается математическая модель контактного взаимодействия деформируемого колеса с недеформируемой опорной поверхностью.
Используется представление колеса в виде абсолютно твердого диска и деформируемого протектора, образованного множеством радиально расположенных упругих стержней [1-3]. Взаимодействие элемента протектора и дороги описывается в рамках модели сухого трения Кулона. Деформация колеса определяется как совокупность деформаций элементов протектора. Сначала рассматривается дискретная модель с конечным числом стержней, затем осуществляется переход к непрерывной модели протектора. Стержневой протектор служит моделью среды, поглощающей энергию и обуславливающей сопротивление качению.
Границы области контакта, участков сцепления и проскальзывания внутри нее, величины и направления сил реакции считаются заранее неизвестными и определяются в ходе исследования в зависимости от жесткостных и геометрических характеристик протектора, а также сил и момента, приложенных к диску колеса.
Сначала решается задача о нагружении деформируемого колеса вертикальной силой в двумерной постановке. Описано равновесие нагруженного колеса, найдена зона контакта и условия возникновения внутри нее участков проскальзывания. Вычислены реакции опорной поверхности. Определены потери энергии на цикле последовательной нагрузки-разгрузки колеса.
Далее рассмотрена трехмерная постановка задачи о нагружении деформируемого колеса. Допускается отклонение плоскости колеса от вертикальной, а также смещения деформированных элементов протектора в произвольных направлениях, в том числе выход из плоскости диска колеса. Получены выводы о влиянии углов развала и схождения на распределение сил в области контакта.
Наконец, изучен ряд задач динамики колеса со стержневым протектором в двумерной постановке. Исследовано движение колеса под действием сил и момента, приложенных к центру диска. Выведены уравнения движения деформируемого колеса. В результате исследования проскальзывания в области контакта получен метод определения типа движения (качение без проскальзывания, качение с частичным проскальзыванием, движение юзом). Изучен стационарный режим движения, при котором линейная и угловая скорость колеса остаются постоянными. Определены условия, необходимые для поддержания заданного стационарного режима движения.
1. Вильке В.Г., Гусак Г.В. Об одной модели армированной шины со стержневым протектором // ПММ. 2011. Т.75. Вып.3. С.435-448
2. Гусак Г.В. Силы реакции при статическом нагружении колесной пары с развалом // Вестн. Моск. ун-та. Сер.1. Математика. Механика. 2018. №4. С.40-47
3. Гусак Г.В. Гистерезисные потери при нагрузке-разгрузке колеса со стержневым протектором // Вестн. Моск. ун-та. Сер.1. Математика. Механика. 2020. №2. С.28-34
Галина Валерьевна Гусак
Механико-математический факультет МГУ имени М.В. Ломоносова, Москва
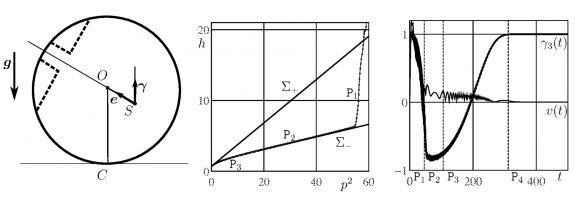
На рисунке: Волчок тип-топ. Диаграмма Смейла. Переворот волчка.
Обсуждается проблема качественного анализа динамики диссипативных механических систем с симметрией на основе обобщенных диаграмм Смейла. Классическая теория Смейла [1] разработана для консервативных механических систем с симметрией. Такие системы допускают интеграл энергии и интегралы Нетер. Критические уровни интеграла энергии на фиксированных уровнях интегралов Нетер образуют в пространстве констант этих интегралов бифуркационное по Смейлу множество. На этом множестве происходят перестройки топологического типа областей возможности движения системы. Очевидно, все точки пространства констант интегралов инвариантны относительно фазового потока системы.
В лекции обсуждается проблема распространения теории Смейла на случай диссипативныхмеханических систем с симметрией [2,3]. В этом случае энергия не возрастает вдоль движений системы. Показано, что критические уровни начального значения энергии на фиксированных уровнях интегралов Нетер по-прежнему задают в пространстве этих постоянных (начальное значение энергии и постоянные интегралов Нетер) бифуркационное по Смейлу множество.Для неконсервативного случая, в отличие от классического случая консервативных систем, инвариантны относительного фазового потока только точки, лежащие на бифуркационном по Смейлу множестве. Все остальные точки эволюционируют вдоль подпространства постоянных интегралов Нетер в сторону уменьшения энергии, асимптотически приближаясь к бифуркационному по Смейлу множеству. Таким образом, обобщенные диаграммы Смейла позволяют находить множество предельных движений диссипативных систем с симметрией по начальному значению энергии системы и значениям интегралов Нетер. Общие результаты иллюстрируются на примерах построения диаграмм Смейла как для консервативных (гироскоп в кардановом подвесе [4]), так и для неконсервативных (волчок тип-топ [3]) систем.
1. Смейл С. Топология и механика. Успехи мат. наук. 1972. Т.27. №2. С.77-120
2. Карапетян А.В. Устойчивость стационарных движений. М.: Эдиториал УРСС. 1998.
3. Карапетян А.В. Глобальный качественный анализ динамики диссипативных систем с симметрией на основе обобщенных диаграмм Смейла. В сб. «Современные проблемы математики и механики»М.: МГУ. 2009. Т.2. Механика. Вып.2.
4. Карапетян А.В., Чаплыгина М.П. Бифуркационный анализ динамики гироскопа в кардановом подвесе. Вестник МГУ. Сер.1. Мат.Мех. 2019. №3. С.73-76.
Александр Владиленович Карапетян
НИИ механики МГУ
В работе рассматривается, как преобразовать механическую энергию в электрическую, для ветроэнергетических установок колебательного типа. В качестве ветроприёмного устройства используется двухзвенный аэродинамический маятник. О его динамике достаточно подробно написано в работах [1-3]. Где, в частности, показано, что при определённых значениях параметров, маятник может совершать периодические движения, с которых возможно снимать энергию. Предполагается, что съём энергии производится с помощью генератора на первом звене, так как ось вращения этого звена неподвижна, в отличие от оси вращения второго звена. Поэтому воздействие генератора вводится, как демпфирование d в первом шарнире.
Для некоторых параметров системы результаты численного моделирования достаточно хорошо количественно согласовывались с экспериментом (V=13 м/с. R=16,5 см). Для таких параметров и была дана оценка энергии, которую можно снимать с данного объекта. При отсутствии пружин на первом звене положение равновесия «по потоку» было асимптотически устойчиво. При увеличении 
– жёсткости пружины на первом звене, частота автоколебаний увеличивалась. Амплитуда первого звена вначале увеличивалась, а затем уменьшалась с ростом . В связи с этим, интересуют параметры, при которых была наибольшая амплитуда колебаний и следующие далее, то есть значения =1.6, 3.2 и 6.4 (подробнее в [2-3]). Менялось лишь значение коэффициента d.
Проведено численное исследование зависимости коэффициента полезного действия 
от параметра d.
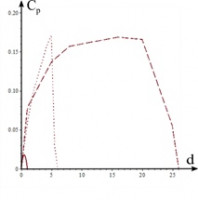
На Рис.1 представлена эта зависимость для трёх пружин, которые были рассмотрены выше. Для случая значение мало, а для 
и 
, в определённом диапазоне достигает значений 0.15-0.17. При этом для диапазон d для «оптимальных» мал, а для 
диапазон d существенно больше. Поэтому введение пружины на первом звене приводит не только к потере устойчивости, но и к увеличению коэффициента .
1. Голуб А.П., Селюцкий Ю.Д. О влиянии жёсткости крепления на динамику двухзвенного аэродинамического маятника // Доклады Академии Наук. 2018. Том 481. №3. С. 254-257
2. Голуб А.П. Экспериментальное исследование упруго-закреплённого аэродинамического двухзвенного маятника // Труды конференции-конкурса молодых учёных НИИ механики МГУ. 2018. С. 77-81
3. Голуб А.П. Диссертация на соискание учёной степени к.ф.-м.н. Динамика двухзвенного аэродинамического маятника // МГУ имени М.В. Ломоносова. 2019.
Андрей Петрович Голуб
МГУ имени М.В. Ломоносова
В докладе рассматриваются новые примеры применения метода асимптотического разделения движений для исследования динамики систем твердых тел. В каждой задаче естественным образом возникает малый параметр, при нулевом значении которого уравнения допускают один или несколько первых интегралов. При возмущении системы значения этих интегралов медленно меняются с течением времени, что позволяет производить качественный анализ решений полной системы.
В задаче о движении экипажа повышенной маневренности с омниколесами выявляется связь между динамической системой, описывающей его движения по инерции [1], и классической задачей неголономной механики о коньке Чаплыгина. Исследуется механизм потери устойчивости прямолинейных движений такого экипажа (по результатам курсовой работы студента механико-математического факультета Я.Э. Минькова).
В задаче о торможении однородного упругого деформируемого цилиндра по полупространству из того же материала [2] рассматривается два варианта возмущений: однородный цилиндра из вязкоупругого материала [3] и неоднородный упругий цилиндр(по результатам курсовой работы студентки механико-математического факультета А.Н. Зотовой). В каждой из представленных задач методом введения быстрых и медленных переменных удается выявить качественные свойства решений возмущенных задач.
Работа выполнена при поддержке гранта РФФИ 19-01-00140.
Александра Александровна Зобова
Московский Авиационный Институт (национальный исследовательский университет)
На заре изучения динамики спутников, в так называемом «спутниковом приближении», то есть в случае, когда размеры спутника значительно меньше расстояния до притягивающего центра, является частичным разделением движения: ориентационное движение спутника вокруг центра масс существенно не влияет на движение Кеплеровского центра масс спутника. В то же время движение центра масс спутника существенно влияет на изменение его положения. Использование истинной аномалии в качестве независимой переменной, вероятно, происходит на основании работы Бине, что дает возможность интегрировать задачу Кеплера и одно из двух тел. Впоследствии аналогичная переменная была применена в задаче о трех телах Леви-Чивита и Нехвилла.
Такое свойство движения центра масс, которое наблюдалось, позволило Белецкому использовать после упомянутой классики истинную аномалию в качестве независимой переменной. Было выведено так называемое «уравнение Белецкого», которое было успешно применено для описания динамических свойств движения спутника по круговой и эллиптической орбитам. Вероятно, необходимость компенсировать колебания спутника, возникающие из-за перераспределения внутренних масс, например смещения экипажа, циркуляции жидкостей, привела к идее принудительного перераспределения масс спутника в зависимости от его положения на Кеплеровской орбите. Начало исследований существования относительных равновесий спутников и их устойчивости при периодическом распределении внутренних масс было найдено в перечисленных выше работах.
В данной работе рассмотрена задача исследования динамики относительного движения спутника с переменными свойствами инерции, объектом исследования является притягивающий центр, неподвижный в пространстве со спутником с пульсирующим тензором инерции. Для решения поставленной задачи были выдвинуты основные предположения: спутниковое приближение (центр масс движется вдоль постоянной предписанной Кеплеровой орбиты) и деформация спутника таковы, что главные центральные оси инерции неподвижны относительно его «твердого» каркаса (меняться могут только величины моментов инерции). После проведения ряда вычислений были получены численные и графические решения в поставленной задаче.
Анастасия Алексеевна Кириенко
Механико-математический факультет МГУ имени М.В. Ломоносова, Москва; НИИ механики МГУ имени М.В. Ломоносова, Москва
В рамках данного исследования был создан лабораторный макет ротора Савониуса. Прототип изучали в аэродинамической трубе НИИ механики МГУ при малых скоростях набегающего потока. Замерялись силы, действующие на ротор, и аэродинамический момент. В процессе эксперимента изменялись значения скорости набегающего потока и угловой скорости вращения ротора (в том числе исследовалось вращение в обратную сторону).
На базе полученных данных предложена модификация модели воздействия потока на ротор типа Савониуса, описанная в работах [1-3]. В рамках такой модели безразмерный коэффициент аэродинамического момента раскладывается в ряд Фурье. Получена зависимость коэффициентов ряда от безразмерной угловой скорости.
Такая модель позволяет существенно упростить проведение параметрического анализа для сложных механических систем, имеющих в своем составе ротор Савониуса. Это достигается благодаря расширению методов, применимых для решения такого рода задач за счет средств теоретической механики. Далее результаты можно уточнить с помощью классических методов теории сплошных сред, дающих более точное количественное совпадение, но слишком ресурсоемких для анализа динамики в широкой области параметров.
1. Мастерова А.А. Моделирование динамики малогабаритной ветроэнергетической установки на базе ротора Савониуса/ Труды конференции-конкурса молодых ученых. 13-17 октября 2017 г. / М.: Издательство Московского университета, 2018. – 140-147 с.
2. Мастерова А.А. Моделирование динамики колесной тележки, приводимой в движение с помощью ротора Савониуса/ Труды конференции-конкурса молодых ученых. 15-17 октября 2018 г. / М.: Издательство Московского университета – 98-105 с.
3. Мастерова А.А. Эмпирический подход к описанию воздействия потока на ротор Савониуса/ Тезисы конференции-конкурса молодых ученых Научно-исследовательского института механики МГУ имени М.В. Ломоносова 21-25 октября 2019 г. – с. 21.
Анна Андреевна Мастерова
