НИИ механики МГУ, Москва
Графическая аннотация – рисунок, привязанный к каждому докладу на сайте конференции, - важный визуальный элемент, разъясняющий в научно-популярном стиле суть научной работы участника конференции. Из быстрого просмотра графической аннотации на сайте конференции каждый участник нашей конференции, не специализирующийся в данной области механики, должен получить общее представление о содержании доклада. Графическая аннотация должна по возможности ответить по крайней мере на один из следующих вопросов:
- В чем заключается суть предлагаемого метода исследования некоторой научной проблемы? В чем состоит актуальность и научная новизна?
- Какова область практического приложения результатов исследований? Какая выгода от использования результатов исследований?
Если не удается подготовить графическую аннотацию, отвечающую на эти вопросы, то в качестве графической аннотации можно использовать цветной рисунок, иллюстрирующий
- результаты расчётов, излагаемых в докладе;
- постановку эксперимента;
- схему исследуемого физического явления;
- другой иллюстративный материал, который будет излагаться в докладе.
Графическая аннотация должна быть рисунком в формате JPEG или PNG, размер которого не превышает 0.5 Мб.
С графическими аннотациями конференций 2017 и 2018 годов можно ознакомиться на сайте нашей конференции.
Оргкомитет
НИИ механики МГУ, Москва
Каждому участнику конференции предоставляется возможность сделать не более одного устного доклада и 1-2 стендовых доклада. На устном докладе участник представляет основное содержание своей работы. Ожидается, что изложение устного доклада даётся в научно-популярном стиле, понятном для широкой аудитории. На стендовых докладах, дополняющих устный доклад, участник делает сообщение о частных узкоспециализированных проблемах и результатах. Продолжительность устных докладов будет определяться исходя из числа участников (но не более 20 минут). Участнику необходимо направить в адрес Оргкомитета отдельную аннотацию для каждого доклада (и устного, и стендовых).
Оргкомитет
Федеральное государственное бюджетное образовательное учреждение высшего образования «Пермский государственный национальный исследовательский университет», Институт механики сплошных сред УрО РАН, Пермь
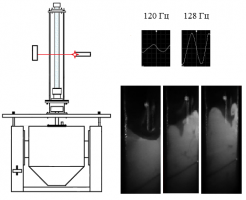
В настоящей работе экспериментально показана возможность визуализации акустических течений в воде и растворах NaCl. Эксперименты проводились в кювете размерами 110×116×160 мм3, имеющей форму прямоугольного параллелепипеда. Кювета была изготовлена из оргстекла толщиной 3 мм. Электродинамический источник ультразвука находился заподлицо с дном кюветы. Для регистрации динамики пузырьков использовалась высокоскоростная камера. Более подробно методика эксперимента и его специфические особенности описаны в статьях [1, 2]. В качестве рабочих жидкостей использовались: дистиллированная вода, водные солевые растворы NaCl с массовым содержанием соли от 0% до 30%.
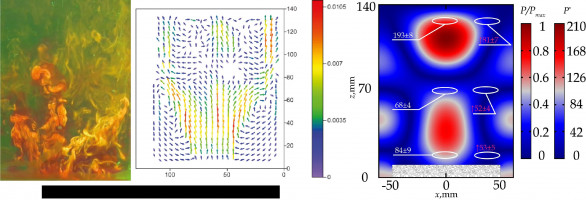
Воздействие горизонтального излучателя УЗ на жидкость сосредоточено в цилиндрическом объёме, в котором выделяют несколько зон в зависимости от расстояния от излучателя. В предварительных экспериментах был использован флюоресцирующий метод визуализации течения. В качестве флюоресцирующего вещества был использован родамин (рис.1, А). Затем, для оценки влияния ультразвукового источника на различные жидкости и растворы был применён метод PIV (Particle Image Velocimetry) - цифровой трассерной визуализации (рис.1, А). Использование данных методов позволило продемонстрировать возможность визуализации акустического течения, а также изучить некоторые его особенности связанные, как показали численные расчеты, с распределением акустического давления в полости ячейки (рис 1, Б). На рис. 1, Б используется две маркерные цветовые шкалы. Первая шкала показывает нормированное на максимальное значение давление, фиксируемое в исследуемой области - P/Pmax. Вторая шкала показывает численное значение среднего значения давления регистрируемого датчиком - P∗. На рисунке 1 наблюдается качественное совпадение течения возникающего в жидкости при визуализации с использованием родамина, PIV, проведённого с использованием метода главных компонент, и численного расчета.
Исследование выполнено за счет гранта Российского научного фонда (проект № 20-69-46066).
1. Козлов М. В., Рыбкин, К. А., Фатталов, О. О., Любимова, Т. П. Динамика парогазовых пузырьков вблизи твердых поверхностей в солевых растворах при дегазации // Теория, эксперимент и новые технологии: конф. (Новосибирск - Шерегеш, 28 февраля-06 марта 2020 г). Новосибирск: Издательство Параллель, 2020. С. 90-91.
2. Rybkin K. A. et al. Experimental study of formation and dynamics of cavitation bubbles and acoustic flows in NaCl, KCl water solutions //Journal of Physics: Conference Series. – IOP Publishing, 2017. – Т. 879. – №. 1. – С. 012026.
Максим Владимирович Козлов
НИИ механики МГУ имени М.В. Ломоносова
Моделируется течение смеси газа и заряженных частиц, с учётом их взаимодействия и электризации, в случае плоской стационарной затопленной струи несжимаемой жидкости в предположении, что движение частиц не влияет на течение несущей среды. При описании движения частиц используется подход Лагранжа: частицы движутся под действием силы тяжести, гидродинамических и электростатических сил. При взаимодействии (соударении) частиц меняются их скорости и заряды. Предполагается, что смесь состоит из частиц двух различных диаметров. В начальный момент распределение частиц определяется их количеством (или размерами занимаемой ими области), общей концентрацией и долей крупных частиц. Проводится детальное исследование влияния параметров распределения на течение смеси в виде затопленной струи и эволюцию электрического поля в процессе течения. Определяются количественные характеристики электрического поля (накопленный частицами заряд, максимальная напряжённость электрического поля и другие). Оценивается количество и начальная концентрация частиц, при которых напряжённость поля достигает критических значений самостоятельного разряда или молнии.
1. Абрамович Г.Н. Теория турбулентных струй. Репринтное воспроизведение издания 1960 г. М.: ЭКОЛИТ, 2011. 720 с.
2. Горохова Н. В. Эволюция электрического поля в течениях смеси газа с заряженными частицами // XII Всероссийский съезд по фундаментальным проблемам теоретической и прикладной механики: сборник трудов в 4 томах. РИЦ БашГУ Уфа, 2019. Т. 4. С. 31–33.
3. Soo S.L. Dynamics of charged suspensions // International reviews in aerosol physics and chemistry. Vol. 2. Pergamon Press, Oxforf. 1971. P. 61-149.
Наталья Владимировна Горохова
Пермский государственный национальный исследовательский университет
Динамика возникающих в жидкости кавитационных пузырьков зависит от различных факторов, могут наблюдаться как коллапс пузырьков, так и их коалесценция и длительное существование относительно крупных пузырьков, как в объеме жидкости, так и вблизи твердых поверхностей [1].
Дегазация жидкости — процесс уменьшения содержания газа в жидкости. На данный момент существуют химические и физические способы дегазации. В основе химических методов удаления из воды, растворенных газов лежит их химическое связывание, достигаемое введением реагентов или фильтрованием через специальные загрузки. Сущность физических методов дегазации заключается в следующем: вода, содержащая удаляемый газ, приводится в соприкосновение с воздухом, если парциальное давление этого газа в воздухе близко к нулю; создаются условия, при которых растворимость газа в воде становится ничтожно малой.
В данной работе рассматривается ультразвуковой способ дегазации жидкости. При ультразвуковой обработке жидкости создается большое количество малых пузырьков, в которые мигрирует растворенный газ и увеличивает размер этих пузырьков. Далее, за счет силы Архимеда пузырьки поднимаются на поверхность воды и высвобождают находящийся внутри газ во внешнюю среду.
В настоящей работе проведены эксперименты по изучению динамики парогазовых пузырьков дрейфующих вблизи твердых поверхностей под действием ультразвука с использованием дистиллированной воды, а также растворами NaCl и KCl с различными концентрациями, для пластин из аморфного кварца, органического стекла и тефлона. Разработана методика оценки площади поверхности пластины покрытой пузырьками.
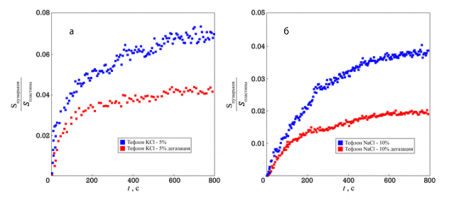
Эксперименты показали, что на скорость роста площади, занимаемой пузырьками, существенно влияет степень дегазации воды. При длительной дегазации воды пузырьковые кластеры на поверхности оргстекла практически не образуются. Однако, на поверхности тефлона можно выделить несколько зон в которых наблюдалось устойчивое прикрепление пузырьков, возможно, вследствие диффузии воздуха с открытой поверхности жидкости в кювете.
Экспериментально подтверждено различие в динамике роста площади, покрытой пузырьками, для тефлона и оргстекла. Результаты работы могут найти применение при объяснении влияния дегазации растворов на качество флотации руд, в частности сильвинитовой руды.
Исследование выполнено за счет гранта Российского научного фонда (проект № 19-31-90138).
1. K. A. Rybkin, Yu. K. Bratukhin, T. P. Lyubimova et al. Experimental study of formation and dynamics of cavitation bubbles and acoustic flows in NaCl, KCl water solutions // Journal of Physics: Conference Series / IOP Publishing. — Vol. 879. — 2017. — P. 012026.
Матвей Максимович Гончаров
ИММ - обособленное структурное подразделение ФИЦ КазНЦ РАН
Серьезной проблемой загрязнения окружающей среды являются выбросы частиц аэрозоля микронного размера, связанные с дымовыми газами сжигания ископаемого топлива, химическим взаимодействием газов, измельчением твердых тел [1]. Для удаления частиц были разработаны различные технологии, такие как электрофильтры, высокоэффективные фильтры, обладающие низкой эффективностью. Ранее были проведены различные исследования резонансных режимов коагуляции и осаждения частиц [2, 3], доказавших свою эффективность в простых установках в виде трубы. Как известно, современные технические системы обладают компактностью и технологически сложностью конструкции. В связи с этим исследуются нелинейные колебания газа и аэрозоля в резонаторах различной формы и размеров.
Исследования ведутся в широком диапазоне частот и амплитуд возбуждения. Получена визуализация процесса осаждения аэрозоля в резонаторе при вынужденных колебаниях среды. Выявлены особенности изменения концентрации частиц от времени при различных начальных концентрациях. Дано сравнение для осаждения аэрозоля в трубе со скачком сечения от осаждения в гладкой трубе в безударно-волновом режиме колебаний.
Исследование выполнено при поддержке РФФИ № 19-01-00442 и гранта президента Российской Федерации (номер гранта МК-297.2020.1).
1. Медников Е. П. Акустическая коагуляция и осаждение аэрозолей. // М.: Изд-во АН СССР. 1963. 263 с.
2. Губайдуллин Д. А., Зарипов Р. Г., Ткаченко Л. А., Шайдуллин Л. Р. Экспериментальное исследование коагуляции и осаждения газовзвеси в закрытой трубе при переходе к ударно-волновому режиму // Теплофизика высоких температур. 2017. Т. 55. № 3. С. 484–486.
3. Губайдуллин Д. А., Зарипов Р. Г., Ткаченко Л. А., Шайдуллин Л. Р. Динамика табачного дыма при резонансных колебаниях в закрытой трубе // Теплофизика высоких температур. 2019. Т. 57. № 2. С. 312-315.
Линар Радикович Шайдуллин
Московский государственный университет имени М.В.Ломоносова
Потоки на склонах, такие как снежные лавины, грязекаменные сели, оползни, подводные мутьевые потоки, в процессе движения разрушают подстилающую поверхность и уносят массу вниз по течению. В случае селевых или подводных мутьевых потоков интерес представляет глубина разрушения склона, так как потоком могут быть разрушены элементы инфраструктуры, изменена форма русла. В случае снежных лавин разрушение подстилающей поверхности изучается для определения изменения массы потока, так как в процессе движения масса потока может измениться в несколько раз, это важно учитывать при проектировании заградительных сооружений.
Для моделирования разрушения потоком и вовлечения в движение материала склона используется многофазный подход. Методом контрольных объёмов рассчитывается движение 3 фаз: материал подстилающей поверхности, материал движущегося потока, воздух. Используется решатель multiphaseInterFoam пакета OpenFOAM. В качестве механизма захвата рассматривается захват при превышении напряжения на дне потока некоторого порогового значения, описанный в работах [1, 2]. Материал потока представлен средой Хершеля-Балкли, использование данного реологического закона позволяет смоделировать процесс отложения материала потока на поверхности склона, а также остановку потока.
Для верификации полученной модели течения рассчитывается снежная лавина в 22 очаге на горе Юкспор (Хибины). Последний раз катастрофическая лавина сошла здесь в 2017 году, тогда были засыпаны автомобильная и железная дороги, выбиты окна в близлежащем доме, погибли 3 человека. В работе используются данные о лавине из этого очага, сошедшей в 1965 году. Для этой лавины известна масса сорвавшегося снега и масса лавинных отложений, что позволяет оценить количество захваченного потоком материала.
Дарья Игоревна Романова
НИИ механики МГУ им. М.В. Ломоносова
Исследуется эффективность газового воздействия на нефтяной пласт, в рамках моделирования смешивающегося вытеснения в пористой среде при закачке углеводородного (УВ) газа. Для описания течения в пористой среде, используется композиционная модель фильтрации, позволяющая учесть изменения компонентного состава жидкостей и газов в пласте, теплофизические свойства которых задаются уравнением состояния Ван-дер-Ваальсового типа. Эффективность нефтеотдачи сравнивается с получаемой при применении традиционной технологии заводнения. Для проведения исследований разрабатывающийся авторами комплекс программ MUFITS [1,2] дополнен модулем для композиционного моделирования фильтрации. На данном примере демонстрируются его обновленные функциональные возможности.
В модели учитывается, что в зависимости от давления и температуры УВ смесь находится либо в однофазном состоянии газа или жидкости (нефти), либо в двухфазном состоянии газ–нефть. Вода же не смешивается с УВ, образуя отдельную компоненту жидкости. Давление во всех фазах считается одинаковым – капиллярное давление пренебрежимо мало, изменение температуры – тоже. Течение происходит в тонком горизонтальном пласте, влиянием силы тяжести пренебрегается.
Рассматриваются модельные составы нефти и вытесняющего газа, совпадающие с одними из предложенных в [3] – случай A. По постановке задача является автомодельной задачей Римана. Её решение состоит из последовательности сильных разрывов (S), на которых рвутся распределения насыщенностей газа sg и воды sw, полные концентрации компонент смеси zi; центрированных волн Римана (R) и областей однородного распределения параметров, распространяющихся от входной границы внутрь области (S4-S3RS2-S1). В случае B в пласт закачивается вода, а решение содержит только один разрыв и одну волну Римана (R*S*) – случай B. Результаты численного моделирования приведены на рис. (рис. Распределения насыщенностей газа и воды в случаях А и B (а) и полных мольных концентраций в задаче А (б), соответственно.)
Исследованы характерные времена, на которых закачка газа позволяет извлечь наиболее ценные УВ компоненты нефти. Показано, что закачка воды в целом более эффективный метод повышения нефтеотдачи из пластов, насыщенных нефтью рассмотренного модельного состава. Газовое воздействие позволяет извлечь дополнительное количество промежуточных компонент УВ ряда только после закачки 3 поровых объемов газа. Однако, это дополнительное количество мало и, по-видимому, не имеет практической значимости. Еще меньший эффект достигается при вытеснении тяжелых компонент.
1. Afanasyev A.A. Hydrodynamic modelling of petroleum reservoirs using simulator MUFITS// Energy Procedia. 2015. V. 76. P. 427–435.
2. Afanasyev A., Kempka T., Kühn M., Melnik O. Validation of the MUFITS reservoir simulator against standard CO2 storage benchmarks and history-matched models of the Ketzin pilot site // Energy Procedia. 2016. V. 97. P. 395–402.
3. Orr F.M. Theory of gas injection processes. Holte, Denmark: Tie-Line Publications, 2007. 381 p.
Елена Анатольевна Веденеева
Центральный аэрогидродинамический институт им. проф. Н.Е. Жуковского, Московский государственый университет имени М.В. Ломоносова

Использование гидрофобных покрытий представляет интерес в широкой области технических и бытовых приложений, в частности в задачах противодействия обледенению летательных аппаратов. Гидрофобные поверхности обладают своеобразными функциональными свойствами, к которым следует отнести водонепроницаемость, стойкость к коррозии, устойчивость к биообрастанию, к неорганическим, а в ряде случаев и к органическим загрязнениям. Благодаря многообразию управляемых свойств создание гидрофобных тел в настоящее время интенсивно развивается. Такие покрытия, как правило, эффективно работают при незначительных числах Вебера, рассчитанных по характерным размерам H рельефа поверхности We = HρV2/σ, (ρ – плотность жидкости, σ – коэффициент поверхностного натяжения, V – скорость удара капли). Однако при превышении поверхностной плотности кинетической энергии (переохлаждённой капли) некого критического значения, льдофобные свойства приводят к отрицательным эффектам ввиду проникновения жидкости в углубления и застывания в них. В случае динамического воздействия свойства гидрофобных/льдофобных покрытий определяются коэффициентами отскока капель в зависимости от числа Вебера. Достоверность полученных результатов обоснована сравнением с теоретическими и экспериментальными оценками других исследователей. Проведены параметрические исследования прилипания жидкости к рельефным покрытиям твердого тела, которые сформированы из комбинации гидрофобных и льдофобных материалов.
Иван Алексеевич Амелюшкин
Институт механики сплошных сред УрО РАН
Моделируется динамика вытеснения одной жидкости другой в капиллярных трубках, используя теорию фазового поля [1]. Корректное описание данной проблемы требует использования теоретической модели, которая учитывает межфазную диффузию. Для этого необходимо отслеживать эволюцию границы раздела двух жидкостей. Кроме этого, граница раздела фаз обладает поверхностным натяжением. Теория фазового поля позволяет учесть данные эффекты. Нами решались уравнения Кана-Хилларда-Навье-Стокса в приближении Буссинеска в переменных скорость-давление с помощью метода дробных шагов (метод проекций) в конечно-разностной постановке. Расчеты, проведенные для одиночного капилляра, согласуются с аналитическими выражениями для скорости кончика мениска и перепада капиллярного давления на границе раздела.
Обнаружено, что для всех рассмотренных конфигураций вытеснение проходит несколько стадий: 1) после установления формы мениска наблюдается поршневое распространение фронта вытеснения через матрицу; 2) когда мениски достигают выходного конца матрицы, некоторый объем вытесняющей жидкости все еще остается на стенках матрицы; 3) наконец, устойчивая стадия достигается, когда вытесненная жидкость все же остается в некоторых элементах матрицы, но дальнейшая перекачка вытесняющей жидкости не приводит к каким-либо различиям в распределении жидкостей в матрице. Показано также, что число Пекле определяет скорость скольжения границы раздела вдоль стен. Найдено, что все интегральные характеристики (включая капиллярное давление), которые характеризуют вытеснение жидкость-жидкость в матрицах разных размеров, сходятся к некоторым кривым, указывая на то, что матрица с размером менее 10x10 элементов достаточна для достаточно точного прогнозирования капиллярного давления в однородной пористой среде.
Сергей Анатольевич Прокопьев
НИИ механики МГУ имени М.В. Ломоносова
Вулканические молнии часто наблюдаются при крупных взрывных извержениях. Они возникают в результате электризации частиц пепла при достижении некоторой критической напряжённости электрического поля. Одной из основных причин электризации частиц является их трение и столкновение. Неоднородность течения оказывает основное влияние на величину накапливаемого частицами заряда и распределение частиц в пространстве. Истечение газо-пепловой смеси из жерла вулкана является сильно неоднородным, турбулентным течением. Наиболее простой моделью такого течения является модель затопленной струи несжимаемой жидкости или газа в плоском или осесимметричном случаях.
В этой работе модель течения смеси газа и заряженных частиц с учётом их взаимодействия и электризации применена для случая плоской стационарной затопленной струи несжимаемой жидкости в предположении, что движение частиц не влияет на течение несущей среды. При описании движения частиц используется подход Лагранжа: частицы движутся под действием силы тяжести, гидродинамических и электростатических сил. Частицы взаимодействуют (соударяются) друг с другом с изменением скоростей движения и зарядов. Заряд, передаваемый при ударе, зависит от упругих и электрических свойств материала частиц, их размеров и скоростей. Исследуется эволюция электрического поля в процессе течения. Проводится оценка количества и концентрации частиц, при которых напряжённость поля достигает критических значений самостоятельного разряда или молнии.
1. Абрамович Г.Н. Теория турбулентных струй. Репринтное воспроизведение издания 1960 г. М.: ЭКОЛИТ, 2011. 720 с.
2. Горохова Н. В. Эволюция электрического поля в течениях смеси газа с заряженными частицами // XII Всероссийский съезд по фундаментальным проблемам теоретической и прикладной механики: сборник трудов в 4 томах. РИЦ БашГУ Уфа, 2019. Т. 4. С. 31–33.
Soo S.L. Dynamics of charged suspensions // International reviews in aerosol physics and chemistry. Vol. 2. Pergamon Press, Oxforf. 1971. P. 61-149
Наталья Владимировна Горохова
НИИ механики МГУ, Москва
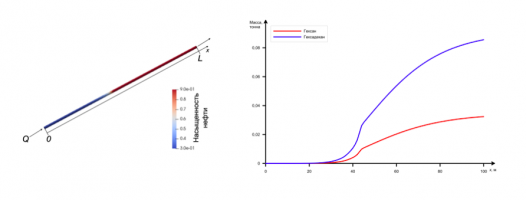
Рассматривается закачка смесей воды, углекислого газа, метана и пропана в геологический пласт, насыщенный нефтью. Исследуется в каком порядке и в течение каких интервалов времени нужно закачивать указанные газы и воду для максимального вытеснения наиболее ценных бензиновых фракций нефти.
Оптимальные режимы закачки газов исследуются в рамках одномерной постановки задачи. Предполагается, что при пласт насыщен нефтью заданного состава. При через границу закачивается вода, углекислый газ, метан и пропан с заданным объёмным расходом , а нефть, таким образом, вытесняется через границу . Определяются составы газов, позволяющие максимизировать для данного момента времени вытеснение наиболее ценных компонент углеводородного ряда. Для определения оптимального состава вытесняющей смеси сначала рассматривается закачка каждого вещества по отдельности, а затем – их смеси. Показано, что вода – более эффективный вытесняющий агент на начальном этапе закачки, однако ряд газов (как, например, CO2) оказываются более эффективными на поздних этапах. Проведены оптимизационные расчеты, позволившие определить наиболее эффективные смеси на различных этапах разработки месторождений.
Для практики представляет интерес вытеснение более тяжелых компонент нефти бензиновой и лигроиновой фракции, использующихся при производстве топлив. Первый рассмотренный состав нефти содержит пентан (C5H12) и пентадекан (C15H32), а второй – гексан (C6H14) и гексадекан (C16H34). Для первого состава была рассмотрена закачка воды, углекислого газа и метана, а во втором случае к этому составу был добавлен пропан. В зависимости от количества закачиваемых поровых объёмов получен оптимальный состав закачиваемого вещества. Отметим, что для второго состава нефти оптимальным оказался состав закачиваемого вещества, не содержащий углекислого газа.
Анна Александровна Чернова
Институт прикладной механики РАН, Москва
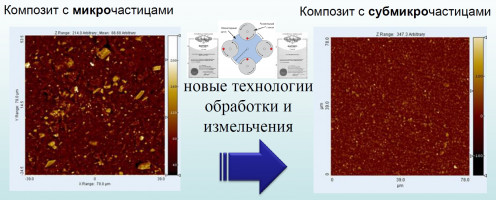
Эластомерные композиты – одни из наиболее перспективных конструкционных материалов, изделия из них широко востребованы и применяются в автомобильной, авиационной, космической, нефтеперерабатывающей и др. промышленности. При создании эластомерных композитов, конструкций и изделий из них в последнее время существенное внимание уделяется вопросам экологии, а также повышению экономической эффективности и энергоэффективности при их производстве. В связи с этим, разработка новых типов упрочняющих дисперсных наполнителей для композиционных материалов, в том числе и природного происхождения, обеспечивающих оптимальный баланс механических свойств композитам и имеющих преимущества по стоимости перед существующими, является актуальной задачей.
Развитие представленного направления исследований включает разработку принципов создания композитных материалов на основе полимерных и эластомерных матриц и нового класса наноструктурированных минеральных наполнителей природного происхождения различного строения (например, шунгит, диатомит, галлуазит, продукты переработки рисовой шелухи и др.), а также исследование особенностей механического поведения и эффектов упрочнения в таких композитах. Предложенные новые исходные материалы для получения упрочняющих наполнителей эластомерных композитов, отличаются от существующих упрочняющих наполнителей (например, техуглерода и коллоидной кремнекислоты), меньшими затратами при получении, экологической безопасностью и, в зависимости от параметров их структуры, позволяют обеспечить полимерным композитам ряд уникальных свойств [1].
Полученные экспериментальные данные показывают на значительный эффект упрочнения до пяти раз при уменьшении среднего размера частиц. Установлено, что наиболее эффективными с точки зрения эффекта упрочнения при применении в качестве наполнителя являются частицы на основе аморфного диоксида кремния, полученные из продуктов переработки рисовой шелухи, и порода шунгит. Показано существенное влияние функциональности поверхности и соотношения углерод/диоксид кремния субмикронных частиц наполнителя на механические свойства эластомерных композитов. Установлено, что новые классы упрочняющих наполнителей в перспективе могут быть рекомендованы для практического применения.
1. Yu. V. Kornev, O.V. Boiko, D.V. Guskov, N.A Semenov. Experimental investigation of the reinforcing effect of organosilane-modified nanodispersed mineral shungite in elastomeric composites. // Composites: Mechanics, Computations, Applications. An International Journal, 2016. -3 (7): - р. 189-200.
Юрий Витальевич Корнев
НИИ механики МГУ
В работе проводится численное исследование вскипания и фрагментации капель перегретой жидкости. В таком состоянии температура жидкости выше температуры насыщения при ее давлении, поэтом в объеме такой капли могут вследствие случайных флуктуаций образовываться микроскопические паровые пузыри. Если размер пузыря больше критического радиуса, то он может расти, в противном случае он мгновенно схлопывается. Рост числа паровых полостей и увеличение их объема может приводить к фрагментации капель жидкости. Изучение этих процессов имеет значение как для фундаментальной науки, так и для ряда технических приложений. Например, такие процессы могут происходить при впрыске криогенного топлива в камеру сгорания силовой установки космического аппарата.
В качестве начального этапа исследования описанных выше процессов в работе рассматривается вскипание и фрагментация одиночной капли перегретой жидкости, находящейся в неограниченной области, заполненной насыщенным паром. В начальный момент времени капля имеет следующие параметры: радиус R0 и степень перегрева S, которая выражается как отношение давления насыщения при температуре капли к давлению окружающей среды. В такой постановке реализуются следующие процессы: испарение жидкости с поверхности капли, образование и последующий рост паровых пузырей в объеме капли.
Математическое описание включает в себя уравнения баланса массы и энергии для капли, а также уравнение идеального газа для паровой фазы. Для описания кинетики объемного вскипания перегретой жидкости используется кинетическое уравнение для функции распределения паровых пузырей по размерам и кинетическое уравнение для нее. Такой подход успешно использовался авторами для моделирования объемной конденсации пересыщенного пара [1]. Скорость образования зародышей паровой фазы описывается согласно классической теории нуклеации [2], а динамика их роста – тепловой энергетической схеме [3]. Массовый и тепловой поток на внешней границе капли вычисляется по соотношениям, полученным методами физической кинетики для свободно молекулярного предела.
В работе предложен критерий разрушения капли перегретой жидкости, основанный на оценке критической объемной доли паровых пузырей и подход, позволяющий определить число и средний размер капель, которые образуются в результате фрагментации.
1. Mayorov V.O., Yastrebov A.K. Numerical study of bulk condensation in laminar flow diffusion chamber // J. Phys. Conf. Ser. 2017. Vol. 891. 012129.
2. Зельдович Я Б К теории образования новой фазы. Кавитация // ЖЭТФ. 1940 Т. 12, №11/12. С.525.
3. Лабунцов Д.А., Ягов В.В. Механика двухфазных систем: Учебное пособие для вузов – М.: Издательство МЭИ, 2000. 374 с.
Вячеслав Олегович Майоров
НИИ механики МГУ имени М.В. Ломоносова
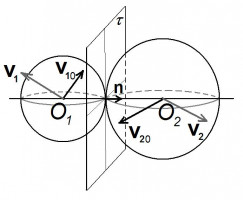
Ранее была построена модель течения смеси газа и заряженных частиц с учётом их взаимодействия и электризации. В качестве взаимодействия частиц рассматривалось их соударение, в результате которого скорости и заряды частиц изменяются. Заряд, передаваемый при ударе, зависит от упругих и электрических свойств материала частиц, их размеров и скоростей. Удар рассматривался как абсолютно упругий, трение между частицами не учитывалось. В этой работе соударение частиц рассматривается как неупругий удар с ненулевым коэффициентом восстановления (когда коэффициент восстановления равен 1, удар является абсолютно упругим). Предполагается, что частицы не коагулируют (случай абсолютно неупругого удара). Учитывается трение между частицами и их вращение. Проводится оценка учёта дополнительных факторов взаимодействия частиц на течение смеси.
1. Горохова Н. В. Эволюция электрического поля в течениях смеси газа с заряженными частицами // XII Всероссийский съезд по фундаментальным проблемам теоретической и прикладной механики: сборник трудов в 4 томах. РИЦ БашГУ Уфа, 2019. Т. 4. С. 31–33.
2. Ландау Л.Д., Лифшиц Е.М. Теоретическая физика – Том 7. Теория упругости. М: Наука. 1987.
3. Soo S.L. Dynamics of charged suspensions // International reviews in aerosol physics and chemistry. Vol. 2. Pergamon Press, Oxforf. 1971. P. 61-149.
Наталья Владимировна Горохова