НИИ механики МГУ имени М.В. Ломоносова
Моделируется течение смеси газа и заряженных частиц, с учётом их взаимодействия и электризации, в случае плоской стационарной затопленной струи несжимаемой жидкости в предположении, что движение частиц не влияет на течение несущей среды. При описании движения частиц используется подход Лагранжа: частицы движутся под действием силы тяжести, гидродинамических и электростатических сил. При взаимодействии (соударении) частиц меняются их скорости и заряды. Предполагается, что смесь состоит из частиц двух различных диаметров. В начальный момент распределение частиц определяется их количеством (или размерами занимаемой ими области), общей концентрацией и долей крупных частиц. Проводится детальное исследование влияния параметров распределения на течение смеси в виде затопленной струи и эволюцию электрического поля в процессе течения. Определяются количественные характеристики электрического поля (накопленный частицами заряд, максимальная напряжённость электрического поля и другие). Оценивается количество и начальная концентрация частиц, при которых напряжённость поля достигает критических значений самостоятельного разряда или молнии.
1. Абрамович Г.Н. Теория турбулентных струй. Репринтное воспроизведение издания 1960 г. М.: ЭКОЛИТ, 2011. 720 с.
2. Горохова Н. В. Эволюция электрического поля в течениях смеси газа с заряженными частицами // XII Всероссийский съезд по фундаментальным проблемам теоретической и прикладной механики: сборник трудов в 4 томах. РИЦ БашГУ Уфа, 2019. Т. 4. С. 31–33.
3. Soo S.L. Dynamics of charged suspensions // International reviews in aerosol physics and chemistry. Vol. 2. Pergamon Press, Oxforf. 1971. P. 61-149.
Наталья Владимировна Горохова
НИИ Механики МГУ, Москва
На активных вулканах часто наблюдаются перемещения поверхности Земли, величина которых может достигать нескольких метров. Периоды подъема и опускания поверхности хорошо коррелируют с периодами повышенной и пониженной вулканической активности [1]. В таких вулканических системах магматический очаг залегает на глубине нескольких километров под поверхностью Земли. При остывании из очага отделяются летучие компоненты, в основном водяной пар и углекислый газ, которые по проницаемым вмещающим породам поднимаются к поверхности. При этом давление и температура жидкости являются источниками напряжений, деформирующих вмещающие породы.
Традиционный полуаналитический подход к моделированию деформаций пород, рассматриваемый в литературе, заключается в том, что каждая ячейка расчетной сетки считается независимым источником деформаций. Для этой ячейки из аналитического решения о нагружении полубесконечной плоскости точечным источником рассчитывается поле перемещений, а полный вектор перемещений в какой-либо точке пространства получается путем суммирования вкладов всех ячеек. Такой подход работает только в предположении плоской поверхности Земли и однородного распределения механических свойств среды по пространству.
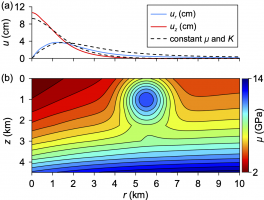
Целью настоящей работы является создание метода, позволяющего рассчитывать деформации пород с учетом механических неоднородностей. Для тестирования этого метода проводится численное моделирование напряженно-деформированного состояния пород в процессе дегазации магматического очага в гидротермальной системе Campi Flegrei. Жидкая и газовая фазы моделируются двухкомпонентной смесью вода-углекислый газ, а твердая фаза, т.е. проницаемые породы, моделируется линейной термопороупругой средой. Расчет фильтрации жидкости и газа производится в симуляторе MUFITS, а расчет напряжений и перемещений пород производится методом конечных разностей в отдельной программе. Обратное влияние деформации пород на механику жидкости не учитывается.
Проведено сравнение нового метода с полуаналитическим подходом, исследовано влияние граничных условий на результаты расчетов. Проведены расчеты деформаций пород для случая неоднородного распределения модуля сдвига и коэффициента Пуассона по пространству. Показано, что в диапазоне значений механических свойств пород, характерных для системы Campi Flegrei, учет наличия неоднородности несущественно влияет на значения перемещений поверхности.
Работа выполнена в рамках проекта РНФ №19-71-10051.
1.Rinaldi A. P., Todesco M., Bonafede M. Hydrothermal instability and ground displacement at the Campi Flegrei caldera // Physics of the Earth and Planetary Interiors. Год 2010. Т. 178. №. 3-4. С. 155-161.
Иван Сергеевич Уткин
НИИ механики МГУ имени М.В. Ломоносова
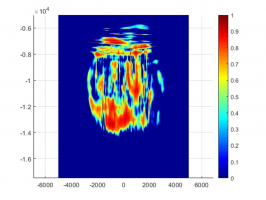
Вулканические молнии часто наблюдаются при крупных взрывных извержениях. Они возникают в результате электризации частиц пепла при достижении некоторой критической напряжённости электрического поля. Одной из основных причин электризации частиц является их трение и столкновение. Неоднородность течения оказывает основное влияние на величину накапливаемого частицами заряда и распределение частиц в пространстве. Истечение газо-пепловой смеси из жерла вулкана является сильно неоднородным, турбулентным течением. Наиболее простой моделью такого течения является модель затопленной струи несжимаемой жидкости или газа в плоском или осесимметричном случаях.
В этой работе модель течения смеси газа и заряженных частиц с учётом их взаимодействия и электризации применена для случая плоской стационарной затопленной струи несжимаемой жидкости в предположении, что движение частиц не влияет на течение несущей среды. При описании движения частиц используется подход Лагранжа: частицы движутся под действием силы тяжести, гидродинамических и электростатических сил. Частицы взаимодействуют (соударяются) друг с другом с изменением скоростей движения и зарядов. Заряд, передаваемый при ударе, зависит от упругих и электрических свойств материала частиц, их размеров и скоростей. Исследуется эволюция электрического поля в процессе течения. Проводится оценка количества и концентрации частиц, при которых напряжённость поля достигает критических значений самостоятельного разряда или молнии.
1. Абрамович Г.Н. Теория турбулентных струй. Репринтное воспроизведение издания 1960 г. М.: ЭКОЛИТ, 2011. 720 с.
2. Горохова Н. В. Эволюция электрического поля в течениях смеси газа с заряженными частицами // XII Всероссийский съезд по фундаментальным проблемам теоретической и прикладной механики: сборник трудов в 4 томах. РИЦ БашГУ Уфа, 2019. Т. 4. С. 31–33.
Soo S.L. Dynamics of charged suspensions // International reviews in aerosol physics and chemistry. Vol. 2. Pergamon Press, Oxforf. 1971. P. 61-149
Наталья Владимировна Горохова
НИИ механики МГУ имени М.В. Ломоносова
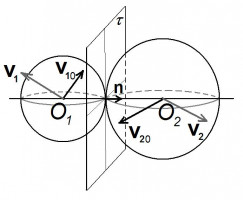
Ранее была построена модель течения смеси газа и заряженных частиц с учётом их взаимодействия и электризации. В качестве взаимодействия частиц рассматривалось их соударение, в результате которого скорости и заряды частиц изменяются. Заряд, передаваемый при ударе, зависит от упругих и электрических свойств материала частиц, их размеров и скоростей. Удар рассматривался как абсолютно упругий, трение между частицами не учитывалось. В этой работе соударение частиц рассматривается как неупругий удар с ненулевым коэффициентом восстановления (когда коэффициент восстановления равен 1, удар является абсолютно упругим). Предполагается, что частицы не коагулируют (случай абсолютно неупругого удара). Учитывается трение между частицами и их вращение. Проводится оценка учёта дополнительных факторов взаимодействия частиц на течение смеси.
1. Горохова Н. В. Эволюция электрического поля в течениях смеси газа с заряженными частицами // XII Всероссийский съезд по фундаментальным проблемам теоретической и прикладной механики: сборник трудов в 4 томах. РИЦ БашГУ Уфа, 2019. Т. 4. С. 31–33.
2. Ландау Л.Д., Лифшиц Е.М. Теоретическая физика – Том 7. Теория упругости. М: Наука. 1987.
3. Soo S.L. Dynamics of charged suspensions // International reviews in aerosol physics and chemistry. Vol. 2. Pergamon Press, Oxforf. 1971. P. 61-149.
Наталья Владимировна Горохова
НИИ механики МГУ им. М.В. Ломоносова, Институт теории прогноза землетрясений и математической геофизики РАН
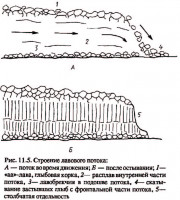
Лавовые потоки зачастую движутся по уже извергнутому ранее материалу, на их поверхности за счет остывания может образовываться «корка», которая растрескивается и обрушивается перед потоком. В результате, в застывших потоках наблюдается подслой в виде лавобрекчии – породы, представляющей собой обломки лавы, ей же сцементированные [1], см. рис. При движении этот подслой, содержащий значительную долю обломков остывшей породы, в значительной мере не сцеплен с подстилающей поверхностью. В простейшей постановке это явление было учтено в рамках осесимметричной модели растекания лавы [2].
Трещинные вулканы, или линейные вулканы, характеризуются тем, что излияние лавы на земную поверхность происходит по протяженным трещинам, они могут иметь вид цепи конусов. Извержения происходят вдоль всей трещины или в отдельных её частях.
В настоящей работе в плоской двумерной постановке рассматривается задача о растекании лавы как несжимаемой неньютоновской жидкости по плоской наклонной подстилающей поверхности – склону от точечного источника. На поверхности ставится обобщенное условие Навье – скорость на поверхности считается степенной функцией трения. Аналогично [2], в приближении тонкого слоя задача сводится к решению одного нелинейного дифференциального уравнения в частных производных второго порядка с интегральным условием. При существенном ограничении на параметры задачи найдено автомодельное решение, в общем случае решение строится численно. Рассматривается влияние параметров задачи на скорость распространения лавовых потоков и их толщину.
Решение такой модельной задачи о течении вязкой жидкости с частичным проскальзыванием представляет интерес не только с точки зрения рассматриваемой проблемы. Частичное проскальзывание встречается для неньютоновских жидкостей, представляющих собой многокомпонентные системы, таких как концентрированные суспензии, эмульсии, гели и т.п., вязкие жидкости проскальзывают вдоль супергидрофобных поверхностей – см., например, [3].
1. Короновский Н. В., Якушова А. Ф. Основы геологии: Учеб. для географ. спец. вузов. М.: Высш.шк., 1991. 416 с.
2. Веденеева Е. А. Растекание лавы во время вулканических извержений при условии частичного проскальзывания на подстилающей поверхности // Изв. РАН. МЖГ. 2015. № 2. C. 27-40.
3. Malkin A. Ya., Patlazhan S. A. Wall slip for complex liquids – Phenomenon and its causes // Advances in Colloid and Interface Science. 2018. V. 257. P. 42-57.
Елена Анатольевна Веденеева
НИИ Механики МГУ, Москва
Перемещение магмы в земной коре в основном происходит в результате образования трещин, называемых дайками, через которые магма поднимается к поверхности Земли [1]. Большая часть даек не достигает поверхности, а останавливается на уровне нейтральной плавучести или блокируется твердыми слоями пород. При локализованном внедрении большого количества даек возникают магматические очаги, то есть области с высокой долей расплавленных пород.
Рост трещины и заполнение ее расплавом сопровождаются деформацией вмещающих пород. В существующих моделях формирования магматических очагов наличие этих деформаций либо не учитывается, либо перемещение пород определяется из упрощенных кинематических соотношений при заданном расположении и размере дайки [2,3].
В настоящей работе предлагается новая модель тепломассопереноса в процессе периодического внедрения магмы во вмещающие породы. В модели учитывается возможность произвольного расположения и ориентации даек в пространстве, а также наличие упругих деформаций вмещающих пород при внедрении даек. Перемещение пород при наличии движущейся магмы описывается аналитическим решением задачи нагружения внутренним давлением трещины, находящейся в бесконечной плоскости. Показано, что при типичных для островодужных вулканов значениях потока магмы формирование очагов возможно в течение сотен лет от начала притока магмы. Проанализировано влияние расхода магмы, размера даек и их ориентации на объем и форму очага.
Работа выполнена при финансовой поддержке РФФИ (проект №18-01-00352).
1.Rubin A.M. Propagation of magma-filled cracks // Annual Review of Earth and Planetary Sciences. Год 1995. Т. 23. № 1. С. 287-336.
2.Annen C. From plutons to magma chambers: Thermal constraints on the accumulation of eruptible silicic magma in the upper crust // Earth and Planetary Science Letters. Год 2009. Т. 284. № 3-4. С. 409-416.
3.Dufek J., Bergantz G. W. Lower crustal magma genesis and preservation: a stochastic framework for the evaluation of basalt–crust interaction // Journal of Petrology. Год 2005. Т. 46, № 11. С. 2167-2195.
Иван Сергеевич Уткин