НЕЙРОННЫЕ СЕТИ В МЕХАНИКЕ СПЛОШНОЙ СРЕДЫ
НИИ механики МГУ имени М.В. Ломоносова
Работа металлических конструкций при повышенных температурах в условиях растяжения иногда приводит к потери устойчивости. Изучение этого процесса при повышенных температурах представляет собой большой интерес, особенно поиск момент локализации деформаций. Известные на сегодняшний день критерии появления локализации деформаций в образце можно разделить на четыре группы: три детерминированных критерия - максимальной силы [1, 2], деформационные [3] и временные критерии [4, 5], а так же критерии, основанные на глубоком машинном обучении [6] и др.
Экспериментальные испытания проводились при постоянной температуре 400°С с постоянной растягивающей нагрузкой в НИИ механики МГУ им. М.В. Ломоносова. Разработанный бесконтактный метод измерения [7] использован для измерения параметров образца. Полученные механические характеристики моделируются градиентным бустингом и нейронными сетями по фотографиям процесса деформирования. Промоделированы: длина образца, деформация образца и время локализации деформаций.
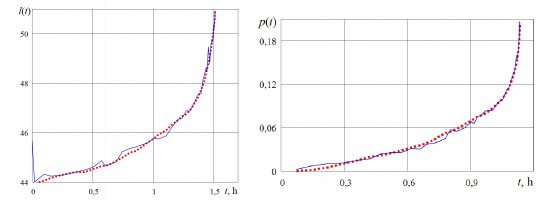
Моделирование методом градиентного бустинга показало, что алгоритм потерял обобщающую способность уже на уменьшенном наборе данных, поэтому в дальнейшем не рассматривался. Пример зависимости p(t) для экспериментов № 13 приведен на рисунке слева.
Нейросетевой анализ продольной деформации дал общую ошибку ~10 %. Для дальнейшего снижения ошибки была построена линейная регрессия на прогнозах трех нейронных сетей с наилучшими наборами гиперпараметров. Это позволило снизить ошибку моделирования до 3,6 % на всей выборке. Пример полученного результата для эксперимента №17 приведен на рисунке справа.
Времена локализации моделировались искусственной нейросетью для размерного и безразмерного значения. Использовались нейросеть с четырьмя выходами и четыре отдельных нейросети с одним выходом. Последняя показала лучший результат – 1.5 % на всей выборке данных.
1.Hora P, Tong L, Berisha B. Modified maximum force criterion, a model for the theoretical prediction of forming limit curves. Int. J. Mater. Form., 2013; 6: 267-279. https://doi.org/10.1007/s12289-011-1084-1.
2. Aretz H. An extension of Hill’s localized necking model. Int. J. Eng. Sci., 2010; 48:312-331.
3. Martínez AJ, Vallellano C, Morales D, Garc-Lomas FJ. On the Experimental Detection of Necking in Stretch‐Bending Tests. AIP Conference Proceedings 1181, 2009; 79: 500-508. https://doi.org/10.1063/1.3273668.
4. Wilshire В, Burt Н. Long-term creep design data for forged ICr—lMo—0,25V steel. Strength, Fracture and Complexity, 2006; 4: 65-73.
5. Srinivas B, Janaki P, Ganesh R. Application of a few necking criteria in predicting the forming limit of unwelded and tailor-welded blanks. Strain Analysis for Engineering Design, 2010; 45(2): 79-96.
6. Applications of Deep Learning for Computer Vision. Retrieved from https://machinelearningmastery.com/applications-of-deep-learning-for-computer-vision; 3 May 2019.
7. Teraud WV. An experimental research of high temperature strain localization and a method for non-touch measurements at a high temperature experiments. In: Proceedings of the First International Conference on Theoretical, Applied and Experimental Mechanics. Structural Integrity. Springer, Cham, 2018; 5: 124-130.