Институт теоретической и прикладной механики им. С.А. Христиановича СО РАН
Прогнозирование качества воздуха в городах сегодня является актуальной задачей. Наличие низких источников загрязняющих веществ от автотранспорта в виде газовых примесей и пылевых аэрозолей в воздухе в окрестности городских застроек приводит к ухудшению экологической обстановки и негативно влияет на здоровье человека. Изучение механизмов переноса примеси в турбулентном течении воздуха в окрестности систем плохообтекаемых тел, имитирующих различные типы застройки, позволяет получить новые данные о структуре течений, распределении концентраций примеси и локальных эффектах, возникающих в потоке. Эти данные могут быть использованы для оценки качества воздуха в городских каньонах и стать основой для разработки рекомендаций об оптимальных геометрических параметрах каньона, расположении фильтрующих и заградительных экранов и других мер снижения концентраций вредных выбросов.
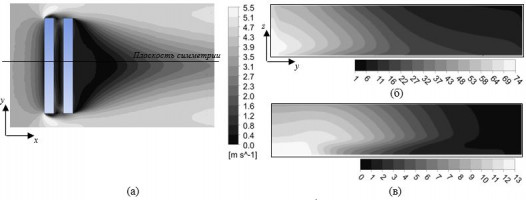
В настоящем исследовании численно решена задача о переносе примеси гексафторида серы SF6, инжектируемой через систему линейных наземных источников, в воздухе в окрестности модельной конфигурации городского каньона с соотношением размеров W/H=1;2;3, где W – ширина каньона, H- высота каньона. Численное моделирование выполнено на основе решения 3D нестационарных уравнений Навье-Стокса, дополненных подходом DDES k-ε Realizable для описания турбулентных эффектов в течении и уравнением переноса для примеси. На первом этапе, для валидации расчетной модели использованы данные эксперимента [1], в котором проведено исследование течения воздуха с примесью в модельном городском каньоне с соотношением сторон W/H=1. По результатам валидации получено хорошее качественное и удовлетворительное количественное соответствие данных расчета и экспериментальных данных по профилям нормализованной концентрации примеси в характерных сечениях модели. На основе численного моделирования дано описание структуры течения среды «воздух-примесь» в окрестности каньона и анализ динамики вихревых структур на различные моменты времени. На втором этапе с использованием численной модели проведено параметрическое исследование влияния соотношения размеров каньона на распределение концентраций примеси вблизи подветренной и наветренной стенок каньона. Показано, что увеличение соотношения сторон каньона W/H приводит к существенному перераспределению примеси и снижению концентраций примеси в пешеходных зонах каньона.
1. Gromke C., Ruck B. Influence of trees on the dispersion of pollutants in an urban street canyon-Experimental investigation of the flow and concentration field // Atmos. Environ. 2007. Vol. 41, № 16. P. 3287–3302.
Светлана Алексеевна Вальгер
Национальный исследовательский Томский государственный университет
В настоящее время существует множество математических моделей лесных пожаров, но только небольшая их часть учитывает вклад горящих и тлеющих частиц в распространение пожара. При этом расчёты основываются на приблизительных характеристиках, так как точных данных до сих пор не существует.
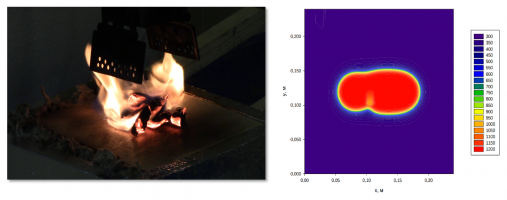
Для тестирования и верификации разрабатываемой математической модели, предложенной в статье [1], для моделирования процесса зажигания древесины горящими частицами, образовавшимися в результате горения фронта низового лесного пожара, была проведена серия экспериментов по определению вероятности воспламенения и времени зажигания образцов древесины в результате одиночной частицы, а также группы частиц. Методика проведения эксперимента и лабораторное оборудование представлены в [2].
В результате математического моделирования зажигания слоя лесных горючих материалов тлеющими сосновыми веточками, а также сравнения с результатами проведенного эксперимента установлено [3], что для инициирования процесса зажигания тлеющая частица должна обладать значительной тепловой энергией. Для частиц малых размеров, запасенного в них тепла оказывается недостаточным для инициирования пиролиза и зажигания температуры. Если размеры частицы достигают критического значения, то в прилегающей к ней области начинается процесс пиролиза. Смешение продуктов пиролиза с атмосферным кислородом приводит к вспышке, сопровождаемой резким, пикообразным ростом температуры. После выгорания газообразных продуктов пиролиза в данной области пространства режим горения сменяется режимом тления. При этом зона пиролиза распространяется во внешнюю по отношению к частице область. Если размеры частицы достаточно большие, то после зажигания слоя ЛГМ возникает режим пламенного горения в газовой фазе.
1.Matvienko O. V., Kasymov D. P., Filkov A. I., Daneyko O. I., Gorbatov D. A. Simulation of fuel bed ignition by wildland firebrands. International Journal of Wildland Fire (2018. Vol. 27, 550-561.https://doi.org/10.1071/WF17083).
2.Тараканова В.А., Касымов Д.П. Изучение в лабораторных условиях взаимодействия горящих и тлеющих частиц природного происхождения с плоской поверхностью различных строительных материалов из древесины //Всероссийская молодежная научная конференция «Все грани математики и механики» : сборник статей. Томск: Издательский Дом ТГУ, 2019. С. 64-76.
3.Kasymov D. P., Tarakanova V. A., Martynov P. S., Agafontsev M. V. Studying firebrands interaction with flat surface of various wood construction materials in laboratory conditions. Journal of Physics Conference Series. 11/2019; 1359:012092., DOI:10.1088/1742-6596/1359/1/012092.
Денис Петрович Касымов
НИИ механики МГУ, Москва
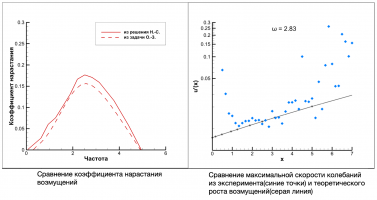
В работе проведено численное исследование линейной устойчивости пространственно развивающейся осесимметричной затопленной струи. Жидкость считается вязкой и несжимаемой. Профиль скорости струи в начальном сечении расчётной области в численном расчёте совпадает с профилем скорости струи на срезе сопла в экспериментальной установке лаб. 103 НИИ механики МГУ. Пространственное развитие струи рассчитывается методом установления путём решения уравнений Навье-Стокса. Исследования устойчивости получаемого таким образом стационарного основного течения выполнены в двух постановках: в рамках решения задачи Орра-Зоммерфельда для серии профилей скорости, соответствующих развивающейся струе на разных расстояниях от сопла, и путём решения уравнений Навье-Стокса, линеаризованных около стационарного решения, описывающего основное осесимметричное течение во всей области развития. В этом случае возмущение с заданной частотой ω и азимутальным номером n задаётся во входном сечении расчётной области, а его эволюция вниз по течению рассчитывается путём решения нестационарных уравнений Навье-Стокса. Расчёты проводились при Re=5700 (число Рейнольдса определяется через среднюю скорость и радиус сопла), совпадающем со значением Re в экспериментах, проводимых параллельно в лаб. 103 НИИ механики МГУ.
Найдены значения коэффициентов нарастания возмущений на различных расстояниях от входного сечения при разных частотах и азимутальных номерах. Получено удовлетворительное согласие результатов в двух рассмотренных постановках. Проведено сопоставление с экспериментальными данными и с результатами анализа устойчивости в рамках уравнения Рэлея.
Работа выполнена при финансовой поддержке РНФ, проект № 20-19-00404 с использованием оборудования Центра коллективного пользования сверхвысокопроизводительными вычислительными ресурсами МГУ имени М.В. Ломоносова и с использованием вычислительных ресурсов ОВК НИЦ «Курчатовский институт», http://computing.nrcki.ru/.
Кирилл Эдуардович Абдульманов
Институт теоретической и прикладной механики им. С.А. Христиановича СО РАН
В настоящее время из-за широкого применения высокоэффективных газообразных топлив для различных энергетических установок большой интерес вызывают исследования связанные с вопросами взрыво- и пожаробезопасностью, а в частности работы направленные на выявление возможности ослабления и подавления газовой детонации, ее инициирования и взаимодействия с различными препятствиями. Уже существует ряд работ, в которых изучалось подавление детонации, например инертными частицами [1]. В настоящей работе для ослабления детонации используется многорядная решетка, состоящая из прутьев круглого сечения, расположенных в шахматном порядке.
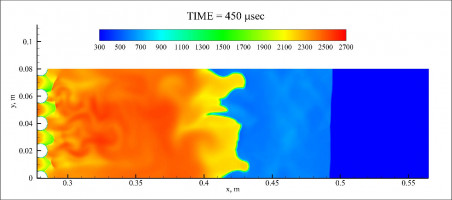
Задача решалась в плоской, симметричной постановке (рис.1). В качестве решателя использован программный комплекс ANSYS Fluent. Используемая математическая модель была ранее протестирована на задаче об инициировании наклонной детонации [2]. Кинетическая схема, включающая одну брутто-реакцию горения водорода в воздухе, была верифицирована по экспериментальным данным о временах задержки воспламенения и скорости распространения детонационной волны при различных условиях [3].
В результате расчета задачи о взаимодействии детонационной волны с цилиндрической решеткой выявлено, что используемая математическая модель, а в частности кинетический механизм химических реакций, учитывает изменение кинетики водорода в области третьего предела воспламенения водорода в воздухе. Увеличение диаметра цилиндров, при неизменной пропускной способности, приводит уменьшению дефицита скорости ДВ несмотря на возрастание длины участка канала, в котором расположено препятствие. Уменьшение геометрических параметров преграды до размеров, сопоставимых с размером детонационной ячейки смеси, приводит к возрастанию ее эффективности для ослабления детонации.
Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 20-38-90178.
1. Tropin, D.A. and Fedorov A.V. Effect of inert micro- and nanoparticles on the parameters of detonation waves in silane/hydrogen - air mixtures // Combustion, Explosion, and Shock Waves. 2019. Vol. 55, No 2. P. 230 - 236.
2. Bedarev I. A., Temerbekov V. M., Fedorov A. V. Simulating the regimes of oblique detonation waves arising at detonation initiation by a small-diameter projectile // Thermophysics and Aeromechanics. 2019. Vol. 26, No 1. P. 59 – 68.
3. I.A. Bedarev, K.V. Rylova, and А.V. Fedorov. Application of Detailed and Reduced Kinetic Schemes for the Description of Detonation of Diluted Hydrogen–Air Mixtures// Combustion, Explosion, and Shock Waves. 2015. Vol. 51, No. 5, P. 528–539.
Валентин Макарович Темербеков