НЕСТАЦИОНАРНЫЙ ИЗГИБ КОНСОЛЬНО-ЗАКРЕПЛЕННОЙ БАЛКИ БЕРНУЛЛИ-ЭЙЛЕРА С УЧЕТОМ ТЕРМОДИФФУЗИИ

Московский авиационный институт НИИ

Для надежной работы ряда технических систем, в том числе летательных аппаратов, очень важным является учет взаимодействия множества различных параметров, характеризующих разнообразие видов внешних воздействий. При этом комплексное описание воздействия нагрузок различной физической природы на конструкцию и её отдельные элементы требует более глубокого понимая сути протекающих при этом процессов. В данной работе на примере нестационарного изгиба свободно опертой балки, как одного из основных элементов строительных конструкций, исследуется взаимосвязь механического, температурного и диффузионного полей.

Рассматриваемый вопрос очень важен при расчете корпусов авиадвигателей, фюзеляжей самолётов и ракет, для которых динамические изменения, связанные с внутренним переносом вещества при воздействии критических температур, и под действием механической нагрузки, могут привести к катастрофическим последствиям. Правильное понимание и применение законов диффузии, теории упругости и законов, описывающих температурное воздействие, позволяет избежать непредсказуемых и нежелательных изменений в авиаконструкциях, происходящих под влиянием нестационарных нагрузок различного характера.

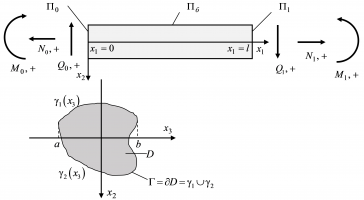
Для постановки задачи используется модель связанной термоупругой диффузии для однородного ортотропного многокомпонентного континуума [1-4]. Модель нестационарного изгиба для упругодиффузионной балки Эйлера-Бернулли строится с помощью вариационного принципа Даламбера [3-5]. При этом предполагается, что:

1.      Поперечные прогибы считаются малыми. Сечения, перпендикулярные к оси балки до деформации, остаются плоскими и после деформации (гипотеза плоских сечений);

2.      Поперечные сечения после деформации остаются нормальными к изогнутой оси балки (гипотеза Бернулли- Эйлера);

3.      Боковая поверхность балки свободна от нагрузок и тепломассоперенос на ней отсутствует, что позволяет считать балку несжимаемой в поперечном направлении.

Для решения полученной задачи, используется интегральное преобразование Лапласа по времени и разложение в ряды Фурье по пространственной координате. Обращение преобразования Лапласа осуществляется аналитически с помощью вычетов и таблиц операционного исчисления. Для расчетного примера, иллюстрирующего взаимодействие физических полей, рассматривается балка прямоугольного сечения, выполненная из трехкомпонентного материала, состоящего из алюминия (93,5%), меди (4,5%) и цинка (2%).

1.Aouadi M., Miranville A. Quasi-stability and global attractor in nonlinear thermoelastic diffusion plate with memory // Evolution equations and control theory. 2015. Vol. 4. No 3. P. 241-263

2.Bhattacharya D., Kanoria M. The influence of two temperature generalized thermoelastic diffusion inside a spherical shell // International Journal of Engineering and Technical Research (IJETR). - 2014. - Vol. 2, Is. 5. - P. 151-159

3. Tarlakovskii D.V., Zemskov A.V. An Elastodiffusive Orthotropic Euler-Bernoulli Beam with Considering Diffusion Flux Relaxation // Math. Comput. Appl. – 2019. – Vol. 24, Is. 1, 23;  doi:10.3390/mca24010023

4. Zemskov A.V., Tarlakovskii D.V. Unsteady Vibration Model of the Euler-Bernoulli Beam Taking into Account Diffusion // IOP Conf. Series: Journal of Physics: Conference Series. – 2019. – Vol. 1158. – 042043  doi:10.1088/1742-6596/1158/4/042043

5.Le, K.C., Vibrations of shells and rods, Springer Verlag, Berlin, 1999

Георгий Михайлович Файкин

• Подробнее...

Решение одномерной нестационарной задачи механодиффузии для сплошного цилиндра методом эквивалентных граничных условий, с учетом релаксации диффузионных потоков.

Московский авиационный институт (национальный исследовательский университет)

В настоящей работе рассмотрена полярно-симметричная задача механодиффузии, состоящая в аналитическом определении параметров НДС (напряженно-деформированного состояния) сплошного одномерного многокомпонентного однородного ортотропного цилиндра, находящегося под действием нестационарных радиальных объемных возмущений. Поверхность цилиндра предполагается свободной от нагрузок и на ней поддерживается постоянный уровень концентрации диффузантов. В задаче учитывается время релаксации диффузионных потоков, подразумевающее конечную скорость распространения диффузионных возмущений. Математическая постановка задачи включает в себя дифференциальное уравнение движения, закон сохранения массы в локальной форме, а также N уравнений массопереноса, вызванного диффузией [1–4].

Решение задачи ищется с помощью метода эквивалентных граничный условий [5]. Для этого рассматривается вспомогательная задача, решение которой получается с помощью интегрального преобразования Лапласа по времени и разложения искомых функций в ряды Фурье по специальным цилиндрическим функциям Бесселя нулевого и первого порядков. Далее строятся соотношения, связывающие правые части граничных условий исходной и вспомогательной задач. Эти соотношения представляют собой систему интегральных уравнений Вольтерра I-го рода. Решение такой системы осуществляется численно с помощью квадратурных формул средних прямоугольников.

1.Deswal S., Kalkal K. K., Sheoran S. S. Axi-symmetric generalized thermoelastic diffusion problem with two-temperature and initial stress under fractional order heat conduction // Physica B: Condensed Matter. – 2016. – Vol. 496. – P. 57–68.

2. Aouadi M. A problem for an infinite elastic body with a spherical cavity in the theory of generalized thermoelastic diffusion // International Journal of Solids and Structures. – 2007. – Vol. 44. – P. 5711–5722.

3. Зверев Н. А., Земсков А. В. Модель механодиффузии для сплошного ортотропного цилиндра с учетом релаксации диффузионных процессов // 19-я Международная конференция Авиация и космонавтика. 23–27 ноября 2020 года. Москва. Тезисы. – Перо Москва, 2020. – С. 458–459.

4. Зверев Н. А., Земсков А. В., Тарлаковский Д. В. Моделирование нестационарных связанных механодиффузионных процессов в изотропном сплошном цилиндре // Проблемы прочности и пластичности. – 2020. – Т. 82, №2. – С. 156–167.

 5. Zemskov A.V., Tarlakovskii D.V. Method of the equivalent boundary conditions in the unsteady problem for elastic diffusion layer // Materials Physics and Mechanics, 2015, No 1, Vol 23, pp. 36–41.

Николай Андреевич Зверев

• Подробнее...