Модель динамики меканум-платформы, учитывающая конструкцию колес, инерционность роликов и поликомпонентное контактное трение
НИУ "МЭИ"
В рамках данного исследования ставится задача построения системы уравнений динамики всенаправленной роликонесущей меканум-платформы с учетом конструкции колес, инерционности роликов и поликомпонентного контактного трения. Актуальность работы обусловлена широким применением всенаправленных платформ и отсутствием моделей динамики меканум-платформ, учитывающих инерционность роликов. При этом известно, что: конструкция колес и модель контактного трения существенно влияют на динамику меканум-платформы [1,2]; а влияние инерционности роликов на динамику омни-платформы показано в [3].
В уравнениях кинематики всенаправленных платформ, составленных при учете реальной конструкции меканум-колес, имеются периодические разрывные функции, которые зависят от углов поворота колес и возникают из-за конечного числа роликов, расположенных на периферии колес, и смены контактирующих роликов (см., например, работу [1]). В связи с указанным обстоятельством при составлении уравнений динамики меканум-платформы с учетом инерционности роликов и конструкции колес возникают проблемы с дифференцированием разрывных функций.
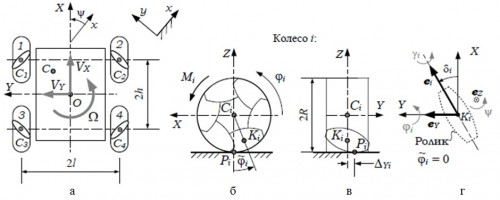
Работоспособность и качество разработанной модели демонстрируется на примере построения уравнений динамики платформы робота KUKA youBot, оснащенной двумя парами меканум-колес. Кинематическая схема указанной платформы изображена на рис. 1.
Рис. 1. Кинематическая схема: (а) – платформа, (б) – меканум-колесо, (в) и (г) – контактирующий ролик.
Для построения уравнений динамики используется формализм Аппеля. При получении инерционных слагаемых во избежание дифференцирования разрывных периодических функций предлагается заменить эти функции их средними значениями. Для нахождения средних значений функций, входящих в уравнения кинематики, используется метод осреднения по фазовым переменным – углам поворота контактирующих роликов. По результатам моделирования показаны отличия в траекториях движения, возникающие при учете инерционности роликов, по сравнению с результатами для модели динамики, не учитывающей инерционность роликов.
1.Adamov B.I., Saipulaev G.R. Research on the Dynamics of an Omnidirectional Platform Taking into Account Real Design of Mecanum Wheels (as Exemplified by KUKA youBot) // Russian Journal of Nonlinear Dynamics. 2020. Vol. 16. № 2. pp. 291–307. DOI: 10.20537/nd200205
2.Б.И. Адамов, А.И. Кобрин, Г.Р. Сайпулаев. Исследование динамики всенаправленной платформы при различных уровнях детализации моделей меканум-колёс и контактных сил // XII Всероссийский съезд по фундаментальным проблемам теоретической и прикладной механики: сборник трудов в 4 томах. Т.1: Общая и прикладная механика. 2019. С. 522–524.
3.К.В. Герасимов, А.А. Зобова. Движение симметричного экипажа на омни-колесах с массивными роликами // Прикладная математика и механика. Т. 82. Вып. 4. 2018. С. 427–440.