Кубанский государственный университет
В последние десятилетия с развитием микро- и нанотехнологий ионоселективные поверхности нашли широкое применение в микроустройствах (например, лабораториях на чипе), что потребовало изучения их свойств в микро- и наномасштабах. Оказалось, что в электролите около таких поверхностей под действием внешнего электрического поля может скапливаться большой заряд, причем толщина заряженного слоя намного превосходит дебаевскую длину. Этот слой назвали зоной пространственного заряда. Пространственный заряд может быть неустойчивым, и при его возмущении развивается тангенциальное электрическое поле, которое приводит к электроконвективному движению [1]. Несмотря на множество практических приложений, наблюдается недостаток теоретических исследований в данной области. В частности, установки наподобие лабораторий на чипе часто не получают широкого распространения из-за невозможности добиться желаемых результатов в рамках изученных явлений. В свою очередь, большинство теоретических работ посвящено исследованию «чистой» электроконвекции, в то время как немногие, включающие в рассмотрение дополнительные эффекты (такие как Джоулев нагрев электролита [2]), показывают, что они могут приводить к качественно новым результатам.
Особенность данной работы заключается в том, что в модель включены дополнительные механизмы переноса электролита: помимо кулоновской силы, приводящей к электрокинетическим эффектам, в систему входит два механизма, связанных с подъемной силой. Первый из них – джоулев нагрев электролита, который приводит к возникновению термоэлектрокинетической неустойчивости [3], второй – это концентрационная конвекция, когда из-за неравномерного распределения соли меняется плотность электролита, и на его поведение начинает влиять сила тяжести [4]. Присутствие трех механизмов неустойчивости вызывает конкуренцию между ними. В работе получены критические значения параметров и составлена карта режимов.
Работа выполнена при частичной финансовой поддержке РФФИ 18-38-00611-мол_а
Наталья Юрьевна Ганченко
Финансовый университет при Правительстве Российской Федерации (Краснодарский филиал)
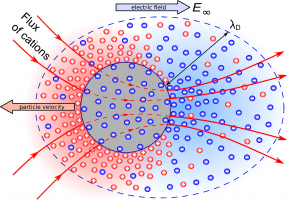
В докладе рассматривается задача движения заряженной микрочастицы с ионоселективной поверхностью в неограниченном объёме, заполненном раствором электролита, под воздействием внешнего электрического поля. В литературе рассмотрены аналогичные задачи для проводящих и диэлектрических частиц, в частных случаях выведены простые формулы типа формулы Гельмгольца-Смолуховского, описывающие зависимость скорости частицы от напряжённости поля. Экспериментально известно, что эта зависимость является линейной при слабых полях (равновесный электрофорез), а при увеличении напряжённости становится ближе к квадратичной (неравновесный электрофорез).
Для решения задачи применяется численное моделирование, которое для слабых и сильных полей дополняется асимптотическим анализом. Аналитически выводится упрощённая зависимость скорости частицы от напряжённости поля, которая отличается от формулы Гельмгольца-Смолуховского. Численно показывается смена режимов электрофореза (от равновесного к неравновесному) при увеличении напряжённости поля. Выводятся основные характеристики поведения электролита - распределения электрического потенциала, заряда и концентрации соли, а также поле скоростей в окрестности частицы. Полученные результаты качественно подтверждаются известными экспериментальными данными как для слабых, так и для умеренных полей. Для очень сильных полей в предложенной авторами модели проявляется разновидность электрокинетической неустойчивости, в результате чего решение с постоянной скоростью движения частицы перестаёт существовать.
В работе также оцениваются перспективы применения найденных режимов поведения частицы для решения технологических задач, описываемых в литературе: конструирования микронасосов, концентрирования и сепарации биологических объектов и т.п.
Работа выполнена в интересах проектов РФФИ (16-08-00643-а) и РНФ (17-79-10343).
Владимир Сергеевич Шелистов
Финансовый университет при Правительстве РФ
Известно, что при эксплуатации ионоселективных поверхностей возникает один из трех токовых режимов: допредельный (омический), предельный или сверхпредельный [1]. Большинство изученных сценариев возникновения сверхпредельных токов были рассмотрены из предположения идеальности ионоселективной мембраны [1, 2], а различные виды неидеальности мембраны рассматривались как небольшие количественные поправки к уже изученным явлениям. Однако, как показали последние исследования [3, 4], в неидеальных мембранах действуют качественно новые механизмы возникновения неустойчивости. Эти механизмы становятся еще более выраженными для концентрированных растворов электролитов, поведение которых гораздо менее изучено. Так, было показано, что наряду с электрокинетической неустойчивостью, которая вызвана электроосмотическим скольжением на границе зоны пространственного заряда, в системе с неидеальной мембраной также присутствует объемная неустойчивость.
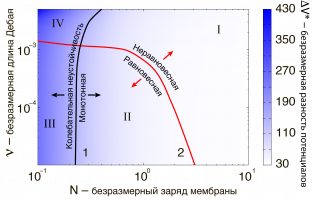
На рисунке представлена карта режимов для двух ключевых параметров: число Дебая ν (отношение толщины двойного электрического слоя к толщине мембраны) и безразмерного заряда мембраны N(отношение заряда мембраны к равновесной концентрации ионов в электролите). На фоне цветом обозначено критическое значение безразмерной разности потенциалов (отношение разности потенциалов и термического потенциала). Кривая 1 разделяет области монотонной (I, II) и колебательной (III, IV) неустойчивостей, а кривая 2 – области равновесной (II, III) и неравновесной (I, IV) неустойчивостей. Для мембран с достаточно большим зарядом, которые близки к идеальным, всегда реализуется только классическая неравновесная электрокинетическая неустойчивость, в то время как с уменьшением заряда мембраны или увеличением концентрированности электролита проявляются новые равновесные и колебательные механизмы неустойчивости.
Работа выполнена при частичной финансовой поддержке РФФИ 18-08-01158-а и Министерства образования и науки Краснодарского края, проект № 16-48-230107-р_а.
Георгий Сергеевич Ганченко
Финансовый университет при Правительстве Российской Федерации (Краснодарский филиал)
В докладе рассматривается задача движения заряженной микрочастицы с ионоселективной поверхностью в неограниченном объёме, заполненном раствором электролита, под воздействием внешнего электрического поля. Такое движение имеет перспективы применения в промышленности, биологии и медицине: для создания микронасосов, микросепараторов и других элементов миниатюрных приборов – "лабораторий на чипе". Исследование такого движения является достаточно сложной задачей из-за наличия эффектов, связанных как с электрофорезом (собственно движением частиц), так и с электроосмосом (движением среды). Наличие неустойчивостей, приводящих к вихреобразованию (которые характерны для электроосмотических течений), порождает интересные эффекты – например, интенсивное перемешивание – но одновременно снижает КПД электрофореза за счёт перераспределения подводимой энергии.
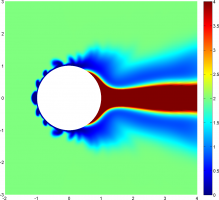
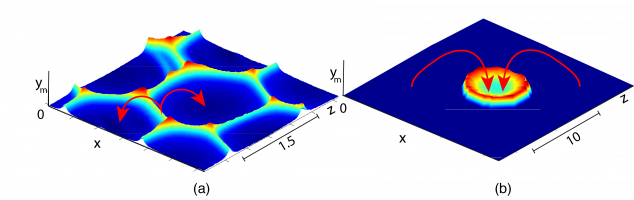
Численное моделирование задачи позволило выявить зависимость критического значения напряжённости внешнего поля, при котором движение электролита теряет устойчивость, от размеров микрочастицы. В отличие от схожей задачи об устойчивости течения в мембранной ячейке, эта зависимость не является монотонной и имеет максимум для частиц диаметром порядка 30 мкм. Неустойчивость приводит к стохастическому движению электролита, схожему с турбулентностью. Окрестность более крупных частиц оказывается подвержена неустойчивости целиком; для более мелких частиц зона неустойчивости сносится потоком и проявляется позади них. В последнем случае также отмечается нарушение монотонности зависимости скорости электрофореза от напряжённости поля вблизи критического значения последней.
Расчёты также показывают, что при большой напряжённости поля происходит накопление соли в узкой области за частицей. Неустойчивость практически не влияет на этот эффект.
Работа выполнена в интересах проектов РФФИ (16-08-00643-а) и РНФ (17-79-10343).
Владимир Сергеевич Шелистов
Кубанский государственный университет
Работа посвящена теоретическому изучению термоэлектрокинетической неустойчивости. Данный тип неустойчивости возникает в электролите около ионоселективных поверхностей при учете Джоулева нагрева электролита вследствие прохождения через него электрического тока [1-3]. В результате линейного анализа устойчивости одномерного решения были обнаружены два типа неустойчивости, которые возникают при различных ориентациях канала относительно силы тяжести: Ra>0 для неустойчивости Рэлея-Бенара, Ra<0 для термоэлектрокинетической неустойчивости.
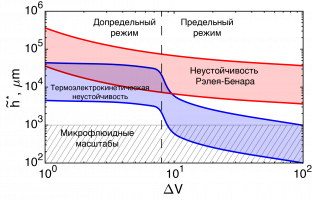
При малых разностях потенциалов, для допредельного режима, абсолютные величины критических значений числа Рэлея имеют одинаковые порядки. При увеличении разности потенциалов ∆V возникает режим предельных токов. Возникновение этого режима обусловлено появлением области пространственного заряда. Именно наличие зоны пространственного заряда является необходимым условием для возникновения классической электрокинетической неустойчивости. Как показывают расчеты, зона пространственного заряда никак не влияет на неустойчивость Рэлея–Бенара. Термоэлектрокинетическая неустойчивость же, напротив, непосредственно связана с проводимостью электролита и наличием объемного заряда, которое порождает скорость электроосмотического скольжения на границе с зоной пространственного заряда. Наличие скорости скольжения действует в совместно с термоэлектрокинетическим конвективным движением, поэтому критическое число Рэлея существенно уменьшается.
Для режима предельных токов критические числа Рэлея для термоэлектрокинетической неустойчивости уменьшаются в тысячи раз, что делает их физически возможными в микронных масштабах. В то же время критические числа Рэлея для неустойчивости Рэлея–Бенара имеют, по сути, тот же порядок, что и для режимов допредельных токов, это подтверждает устоявшееся мнение, что в задачах микрофлюидики неустойчивость Рэлея–Бенара не проявляется.
Работа выполнена при частичной финансовой поддержке РФФИ 18-38-00611-мол_а и Министерства образования и науки Краснодарского края, проект № 16-48-230107-р_а.
Наталья Юрьевна Ганченко
Финансовый университет при Правительстве РФ
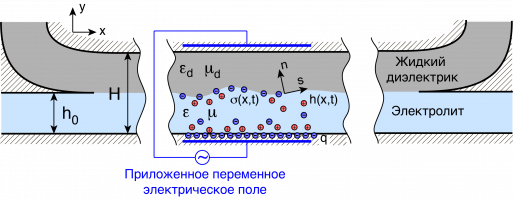
В данной работе рассматривается двухслойная система электролит-диэлектрик со свободной поверхностью раздела под действием внешнего электрического поля. Неустойчивость поверхности раздела является ключевым механизмом, ответственным за перемешивание. В микромасштабах отсутствует классическая гидродинамическая турбулентность, и для эффективного перемешивания в таких условиях необходимо искать другие эффекты, вызывающие неустойчивость одномерных течений и формирование микровихрей.
Для приведения жидкости в движение в микромасштабах обычно используют электрическое поле: оно действует на ионы солей, растворенных в жидкости, и приводит к электроосмотическому течению. Задача перемешивания жидкостей, в принципе, может быть решена аналогично: необходимо только подобрать условия, при которых электроосмотическое течение теряет устойчивость [1]. Существуют и другие способы создания неоднородности, в том числе за счет переменного электрического поля, направленного перпендикулярно каналу с жидкостями [2]. Переменное электрическое поле, особенно высокочастотное, является, к тому же, более предпочтительным по сравнению с постоянным, потому что при этом удается избежать нежелательных химических реакций, приводящих к деградации электродов и появлению пузырьков газа. Для случая, когда электрическое поле направлено вдоль границы раздела, было обнаружено два типа неустойчивости: длинноволновый и коротковолновый, связанные с поверхностными и объемными силами соответственно [3]. Если электрическое поле направлено по нормали к свободной поверхности раздела, то возникает неустойчивость, схожая с неустойчивостью Тонкса-Френкеля [4]. Для случая высокочастотных электрических полей получены асимптотические результаты.
Работа выполнена при финансовой поддержке Совета по грантам Президента Российской Федерации, грант для молодых кандидатов наук МК-5302.2018.1 и РФФИ грант 18-58-15004-НЦНИ_а.
Георгий Сергеевич Ганченко