Объединенный институт высоких температур Российской академии наук, Москва
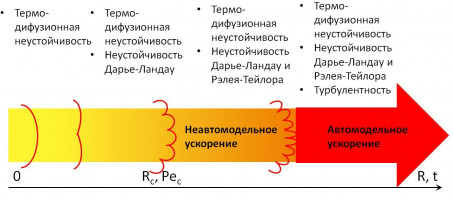
Расширяющиеся фронты химических реакции имеют отношение к процессам в двигателях с искровым зажиганием, к проблемам предотвращения взрывов, а также таких космических явлений, как термоядерное горение в сверхновых. При воспламенении горючей смеси газов в районе точки зажигания, возникает сферическое пламя. Сразу после зажигания пламя является гладким и сферическим. С увеличением размера фронт пламени деформируется и ускоряется. Ускорение фронта пламени является сложным процессом под действием теплового расширения, различных неустойчивостей–гидродинамических, термо-диффузионных, термо-акустических и турбулентности. Когда фронт пламени достигает критического значения Pe, его ускорение становится неавтомодельным, а затем автомодельным. Величина Pe представляет собой отношение радиуса фронта пламени к толщине фронта пламени. Л.Д. Ландау показал, что пламя становится неустойчивым к возмущениям всех длин волн при Re > 1. А.Г. Истратов и В.Б. Либрович показали, что пламя становится неустойчивым при Re > 103-104. Они учитывали влияние химической кинетики, диффузии и теплопроводности и показали, что эти процессы препятствуют развитию возмущений с малой длиной волны. На сегодняшний день существует множество методов моделирования ускорения пламени, как аналитических (фрактальный подход, анализ неустойчивостей, статистический турбулентный подход Колмогорова-Обухова…) так и численных (RANS, LES, DNS…).
Работа выполнена при поддержке Российского Научного Фонда, грант №14-50-00124
Виктор Владимирович Голуб
Объединенный институт высоких температур РАН, Москва, Россия
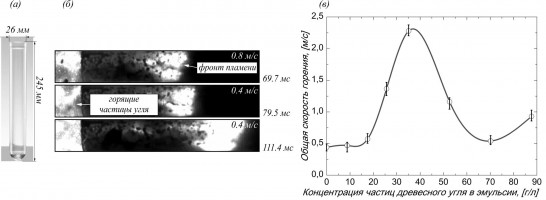
Одним из перспективных видов топлив, позволяющих использовать водонасыщенные углеводороды, является вспененная эмульсия [1, 2]. По своей сути вспененная эмульсия - это пена, состоящая из пузырей кислорода, диспергированных в эмульсии. В данной работе рассматривается процесс горения вспененной эмульсии в полуоткрытой трубке (рис. 1а), в состав которой входят микрочастицы древесного угля (рис. 1б). Использование частиц древесного угля позволяет регулировать скорость распространения пламени во вспененной эмульсии в достаточно широком диапазоне (рис. 1в). Важную роль при распространении пламени в пене играет процесс взрывного вскипания жидкой фазы [3]. С одной стороны, влияние микрочастиц древесного угля на скорость горения пены связано с тем, что горящие частицы угля способствуют повышению температуры во фронте пламени, а, следовательно, и интенсивности взрывного вскипания жидкой фазы. С другой стороны, частицы древесного угля ответственны за более тонкое диспергирование воды в процессе распада пены, что наоборот, приводит к росту потерь тепла из зоны горения. Конкуренция между этими процессами определяет немонотонный характер зависимости скорости распространения пламени от концентрации частиц угля (рис. 1 в).
Рис. 1. (а) Рабочая трубка, в которой осуществлялось измерение скорости распространения пламени. (б) Структура зоны горения (время измеряется с момента воспламенения пены; мгновенные значения скорости пламени представлены для каждого момента времени). (в) Зависимость общей скорости горения от концентрации частиц древесного угля в эмульсии: пена была приготовлена с использованием изооктана (1 мл), воды (1.6 мл), детергента (0.9 мл), перекиси водорода (1.5 мл) и аммиачного раствора сульфата меди (0.7 мл, 1.05 моль/л), средний диаметр частиц древесного угля 67 мкм.
Работа поддержана грантом Российского Научного Фонда No. 17-19-01392.
Литература
[1] B. Kichatov, A. Korshunov, K. Son, E. Son, Combustion of emulsion-based foam, Combust. Flame 172 (2016) 162-172.
[2] B. Kichatov, A. Korshunov, A. Kiverin, E. Son, Methods for regulation of flame speed in the foamed emulsion, Combust. Sci. Technol. 189 (2017) 2095-2114.
[3] А.И. Леонтьев, Б.В. Кичатов, А.М. Коршунов. 2017. Горение вспененных эмульсий. Москва, Издатель: Российская академия наук.
Алексей Михайлович Коршунов
Томский государственный университет
В настоящей работе численно решена задача искрового зажигания аэровзвеси порошка алюминия. Целью работы являлось определение критических условий зажигания порошка алюминия в зависимости от размера и массовой концентрации частиц. Постановка задачи основана на физико-математических постановках [1 – 2].
Математическая постановка задачи определяется системой уравнений, записанной в цилиндрической системе координат, и состоящей из уравнений неразрывности для газа, сохранения импульса и энергии для газа и частиц, баланса массы кислорода и частиц в смеси, уравнений счетной концентрации частиц и состояния газа. В уравнениях, определяющих математическую постановку задачи, правые части, отвечающие за химическое взаимодействие газа и частиц, определяются через радиус алюминия в частице, слагаемые, определяющие инерционное и тепловое взаимодействие определяются через радиус самой частицы, состоящей из алюминия и оксидного слоя. Радиус частицы и радиуса алюминия, оставшегося в частице после выгорания, определялись согласно [2].
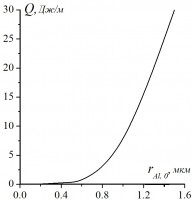
Задача решалась численно с использованием методов [3 – 4]. Метод решения и выбор расчетной сетки соответствовали работе [1]. В расчетах варьировались начальный радиус частиц алюминия и начальная массовая концентрация порошка на единицу объема. Из расчетов определялась минимальная энергия искры, необходимая для зажигания и дальнейшего распространения фронта горения по аэровзвеси. Пример полученных результатов расчета представлен на рис. 1.
На рис. 1 представлена зависимость минимальной энергии искрового зажигания от начального размера частицы алюминия. Видно, что для радиуса частицы меньше 0.5 мкм минимальная энергия искрового зажигания стремится к одному и тому же значению.
В работе было выполнено исследование влияния массовой концентрации порошка на минимальную энергию искрового зажигания аэровзвеси алюминия. Получено, что увеличение массовой концентрации порошка приводит к уменьшению минимальной энергии искрового зажигания.
Исследование выполнено за счет гранта Российского научного фонда (проект №17-79-20011).
1.Моисеева К. М., Крайнов А. Ю. Численное моделирование искрового зажигания аэровзвеси угольной пыли// Физика горения и взрыва. 2018. Т. 54. № 2. С. 61–70.
2.Порязов В.А., Крайнов А.Ю., Крайнов Д.А. Математическое моделирование горения пороха Н с добавлением порошка алюминия// Инженерно-физический журнал. 2015. Т. 88. № 1. С. 93-101.
3.Годунов С.К., Забродин А.В., Иванов М.Я., Крайко А.Н., Прокопов Г.П. Численное решение многомерных задач газовой динамики. – М.: Наука, 1976.
4.Крайко А.Н. О поверхностях разрыва в среде, лишенной ‘собственного' давления// Прикладная математика и механика. 1979. Т. 43. № 3. С. 500-510.
Ксения Михайловна Моисеева
Национальный исследовательский Томский государственный университет
В лабораторных условиях исследовано воздействие очага горения, смоделированного лесным горючим материалом (хвоя сосны), на плоские деревянные образцы различного сорта (сосна, осина, лиственница) с применением ИК-диагностики. В результаты получены профили температуры на поверхности образцов древесины, определены теплонапряженные участки при воздействии модельного очага горения, имитирующего низовой лесной пожар слабой интенсивности.
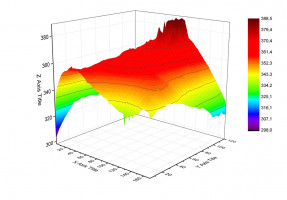
В инфракрасной области характеристики поверхности образца регистрировались с помощью тепловизора JADE J530SB с применением оптического фильтра 2.5–2.7 мкм, который позволял измерять температуру в интервале 310–550 ⁰С. Для регистрации температур в интервале 100–200 ⁰С съемка производилась без оптического фильтра. Частота съемки составляла 50 кадров/сек. Влажность образцов контролировалась с помощью анализатора влажности AND MX-50 с точностью 0.01 %, масса образцов – электронными весами AND HL-100. Схема проведения эксперимента рассмотрена в [1].
Для того чтобы определить теплонапряженные участки на поверхности образца древесины, с помощью программного обеспечения Altair, на термограмме поверхность образца покрывалась прямыми горизонтальными линиями. Расстояние между ними было фиксированное.
Длина горизонтальных линий l соответствовала размерам исследуемого образца древесины. Для каждого отрезка был получен столбец температур, определенных в каждом пикселе соответствующей прямой. В результате, зная геометрическое положение прямых и значения температур, были получены графики распределения температуры на поверхности исследуемого образца, а также установлены теплонапряженные участки на поверхности моделей деревянных конструкций в результате воздействия фронта низового лесного пожара.
Работа выполнена при финансовой поддержке Гранта Президента РФ № МК – 3885.2018.8
Список литературы:
1. Касымов Д.П., Лобода Е.Л., Якимов А.С., Агафонцев М.В., Лобода Ю.А. Экспериментальное и численное моделирование воспламенения модели деревянного ограждения при тепловом воздействии фронта природного пожара / В книге: XXIX Международная научно-практическая конференция, посвященная 80-летию ФГБУ ВНИИПО МЧС России Материалы конференции. В 2-х частях. 2017. С. 201-204.
2. D. Kasymov, M. Agafontsev Investigation of the Fire Hazard Characteristics of Wood Using Infrared Thermography // Proceedings of the 8th European Combustion Meeting. Dubrovnik, Croatia, 2017. p. 1484–1488. URL: http://www.adriacombustioninstitute.org/ecm2017/ (дата обращения: 29.09.2017).
Денис Петрович Касымов
Центральный институт авиационного моторостроения имени П.И. Баранова
Выполнено сравнение термических коэффициентов полезного действия и удельных тяг и импульсов прямоточных реактивных двигателей разных типов с медленным ("дефлаграционным") горением (МГ) и с горением в движущихся (пульсирующих и вращающихся – «спиновых») и неподвижных детонационных волнах (ДВ). Актуальность такого сравнения обусловлена распространенными, особенно в последнее время, утверждениями о возможном увеличении тяговых характеристик воздушно-реактивных двигателей (ВРД) с горением в ДВ (в первую очередь, в пульсирующих – PDE и вращающихся – RDE) на десятки процентов в сравнении с прямоточными ВРД (ПВРД) с МГ при постоянном давлении в дозвуковом потоке. Подобные прогнозы, однако, опираются не на прямой расчет тяг этих двигателей, а на сравнение их идеальных термических коэффициентов полезного действия (кпд) – hth и на применимые только к стационарным течениям в инерциальных системах координат формулы, связывающие также идеальные удельные тяги и импульсы с идеальными кпд. Для PDE эти формулы неверны из-за нестационарности течения.
В России утверждения о преимуществах детонационного горения (ДГ) нередко сопровождаются ссылками на заметку Я.Б. Зельдовича [1] 1940 г., переведенную на Западе только в начале XXI века. Для незнакомых с этой заметкой ссылки на столь авторитетного ученого производят требуемый эффект в противоположность тому, что писал сам автор. Хотя Я.Б. Зельдович обнаружил некоторое увеличение термического коэффициента полезного действия (КПД) при ДГ, это не вызвало у него эйфории. Напротив, в той же заметке высказаны только скептические соображения о применении ДГ, например: "... поиски циклов с ДГ в погоне за небольшим увеличением принципиально достижимого кпд бесперспективны". Ни в этой, ни в других публикациях Я.Б. Зельдовича высказываний в поддержку ДГ нет.
В развитие [1, 2] выполнен термодинамический анализ разных типов ВРД с ДГ и МГ. В исследуемых далее ВРД горению почти всегда предшествует сжатие в воздухозаборнике поступающего из атмосферы со скоростью V0 воздуха и всегда заканчивается "расчетным" расширением в сопле продуктов сгорания до давления набегающего потока р0. В рассматриваемых моделях двигателей предварительное сжатие воздуха в воздухозаборнике и расширение продуктов сгорания в сопле принимаются изэнтропическими и стационарными. По определенным, как в [2], идеальным термическим кпд (hth) находится отношение Ve/V0, где Ve – скорость на выходе из сопла при расчетном расширении до р0. Удельные тяга и импульс пропорциональны разности (Ve/V0 – 1). Рассмотренные типы ВРД включают двигатели с МГ при постоянном давлении, как в ПВРД (по циклу Брайтона), и постоянном объеме (по циклу Хэмфри), пульсирующие детонационные двигатели (PDE) с горением в ДВ Чепмена - Жуге (ДВCJ), ВРД с горением в стационарных ДВCJ, в том числе, с предварительным торможением сверхзвукового потока (SDEy³1, y = Т3/Т0, Т0 и Т3 – температуры холодного воздуха и горючей смеси перед ДВ) и в косой ДВ – SDEOSW (при y = 1).
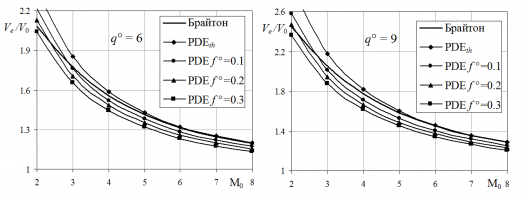
При фиксированных показателях адиабаты воздуха, горючей смеси и продуктов сгорания идеальные характеристики рассмотренных ВРД, предполагающие, как в [2], отсутствие потерь при торможении воздуха в воздухозаборнике, его смешении с газообразным топливом и истечении продуктов сгорания из реактивного сопла, зависят от двух безразмерных параметров: числа Маха полета М0 и q° = q/(cpT0) – безразмерной теплотворной способности горючей смеси (ср – теплоемкость при постоянном давлении). При q° = 6 и 9 сравнение идеальных кпд hth и рассчитанных по hth с помощью упомянутых выше формул (незаконных для PDE) идеальных удельных тяг и импульсов всех рассмотренных двигателей выполнено для М0 от 0.3 до 8. Для этих q° и М0 по такой идеальной тяге PDE незначительно превосходит ВРД с горением при постоянном объеме (по циклу Хэмфри), а ПВРД с МГ – намного только при М0 < 1.5. С ростом М0 превышение идеальной тяги PDE над идеальными тягами других ВРД за исключением SDEOSW быстро уменьшается. Так, при q° = 6 и 9 превосходство по идеальной тяге PDE над остальными становится малым при увеличении числа Маха полета М0.
Пусть PDE имеет n цилиндрических, синхронно работающих групп детонационных камер (ДК) с мгновенно открывающимися и закрывающимися клапанами (входными силовыми стенками). При открытых клапанах в ДК поступает идеально перемешанная горючая смесь. Период работы одной ДК PDE можно разбить на несколько этапов: 1. Открытие клапана, заполнение ДК горючей смесью, мгновенные закрытие клапана и инициирование ДВ волны у входного конца ДК; 2. Приход ДВ на правый конец ДК – сечение входа в идеально регулируемое реактивное сопло; 3. ДВ отражается от правого частично открытого сечения ДК (сужения сопла) как ударная волна (УВ), которая движется к закрытому входному сечению ДК. Далее нестационарные ударные волны, двигаясь по ДК, могут несколько раз отразиться от ее концов. Несмотря на затухание, отражающиеся УВ – не учитываемый при определении идеальных характеристик PDE источник роста энтропии. Клапан мгновенно открывается, когда среднее давление продуктов сгорания в ДК становится меньше давления заторможенного воздуха и идеально перемешанного с ним топлива в объеме перед клапаном.
Истечение продуктов сгорания происходит на протяжении всего цикла работы PDE. Течение в расширяющейся части сопла квазистационарное и изэнтропическое, площадь выходного сечения сопла идеально регулируемая. Расчёты проводились в рамках одномерной задачи в приближении уравнений Эйлера. Система уравнений одномерной нестационарной газовой динамики численно решалась с помощью явной монотонной распадной разностной схемы второго порядка (для гладких решений) по пространственной координате х и по времени t. Второй порядок по времени обеспечивался привлечением схемы Рунге - Кутты. При заданных f ° (отношении площади критического сечения сопла к площади поперечного сечения ДК), М0 и q° в течении периода работы ДК PDE отношение скоростей Ve/V0 получается как функция времени. Его интегрирование по периоду дает средние значения Ve/V0 и тяговые характеристики с учетом нестационарности и неизэнтропичности течения продуктов сгорания в детонационной камере.
На рисунке приведены кривые отношений Ve/V0 для ПВРД (цикл Брайтона, от времени не зависит) и для PDE: посчитанных по идеальному термическому кпд (PDEth) и для нескольких значений f °, найденных в рамках описанной выше нестационарной модели. Видно, что в типичных ситуациях ПВРД лучше многокамерных PDE с вращающимся клапаном (для f °= 0.3 и 0.1 – при М0 ³ 2 и М0 ³ 3). Согласно [3] тяговые характеристики ПВРД заведомо лучше тяговых характеристик и однокамерного PDE, предложенного в [4]. По этим характеристикам уступают ПВРД и все рассмотренные выше ВРД с горением в стационарных ДВ. Из еще не рассмотренных "детонационных" ВРД в последнее время особое внимание уделяется двигателям с вращающейся или спиновой ДВ (RDE). Одно из объяснений такого внимания – переход к стационарному течению во вращающейся со скоростью ДВ системе координат и последующие рассуждения с сохраняющейся в стационарных потоках полной энтальпией. При этом, правда, забывают, что в координатах, вращающихся с угловой скоростью w, вдоль линий тока сохраняется не "обычная" полная энтальпия H, а разность H °= H – (wr)2/2. В кольцевой камере сгорания RDE произведение wr равно скорости детонационной волны. Поэтому величина w так велика, что любые изменения радиальной координаты r при истечении продуктов сгорания заведомо исключают возможность определения отношения Ve/V0 через hth ВРД с ДГ. В противоположность этому, в силу сохранения H удельный импульс Isp RDE с сужающимся центральным телом и цилиндрической "внешней" образующей сопла заметно уменьшится. То что это так, подтверждают низкие значения Isp, рассчитанные в [5] для четырех вариантов RDE, летящих с М0 = 5 в однородной стехиометрической смеси водорода и воздуха с параметрами атмосферы Земли на высоте 20 км. Эти значения Isp = 1990, 2350, 2300 и 2250 с "традиционно" для авторов [5] (см. [3]) завышены: определяя Isp, они почему-то не учитывают сопротивления наветренной части центрального тела воздухозаборника. Исправленные значения Isp близки к 1420, 1830, 1780 и 1720 с, однако даже завышенные величины Isp заметно меньше Isp ПВРД, который при тех же условиях по оценке авторов [3] равен 3500¸3900 с. Дополнительное возрастание энтропии в RDE также имеет место – в УВ, примыкающей к ДВ на границе свежей горючей смеси и продуктов сгорания. Правда, интенсивность этой УВ невелика.
Итак, утверждения о возможном увеличении тяговых характеристик ВРД на десятки процентов благодаря использованию ДГ необоснованны. Даже для дозвуковых и малых сверхзвуковых чисел Маха полета, на которых ВРД с МГ может по тяговым характеристикам уступать PDE, последние заведомо уступают ТРД с МГ. Поэтому преимущества ВРД с ДГ, если и возможно, то не по тяговым характеристикам, а по простоте конструкции (как при малых М0 по сравнению с ТРД) или по меньшей теплонапряженности тракта двигателя (напротив, при больших сверхзвуковых числах Маха М0 > 5 в сравнении c пульсирующим детонационно-дефлаграционным двигателем [6]).
Работа выполнена при поддержке РФФИ (проект 17-01-00126).
Рисунок: кривые Ve/V0 ПВРД (цикл Брайтона) и PDE, рассчитанные по идеальному кпд (PDEth) и по нестационарной модели
1. Зельдович Я.Б. К вопросу об энергетическом использовании детонационного горения // ЖТФ. 1940. Т. 10. Вып. 17. С. 1453-1461.
2. Heiser W.H., Pratt D.T. Thermodynamic Cycle Analysis of Pulse Detonation Engines // J. of Propulsion and Power. 2002. V. 18. No. 1. P. 68-76.
3. Егорян А.Д., Крайко А.Н., Пьянков К.С., Тишин А.П. О расчете характеристик импульсного детонационного двигателя и их сравнении с характеристиками ПВРД // Теплофизика и аэромеханика. 2016. Т. 23. № 2. С. 307-310.
4. Remeev N.Kh., Vlasenko V.V., Khakimov R.A. Analysis of operation process and possible performance of the supersonic ramjet-type pulse detonation engine // Pulse and continuous detonation propulsion / Eds. G. Roy, S. Frolov. Moskow: TORUS PRESS, 2006. P. 235-250.
5. Дубровский А.В., Иванов В.С., Зангиев А.Э., Фролов С.М. Трехмерное численное моделирование характеристик прямоточной воздушно-реактивной силовой установки с непрерывно-детонационной камерой сгорания в условиях сверхзвукового полета // Химическая физика. 2016. Т. 35. № 6. С. 49-63.
6. Крайко А.Н., Александров В.Ю., Александров В.Г. и др. Способ организации горения топлива и детонационно-дефлаграционный пульсирующий прямоточный воздушно-реактивный двигатель. 2016. Патент РФ № 2585328.
Александр Николаевич Крайко
Объединенный институт высоких температур Российской академии наук, Москва
Неустойчивость фронта пламени – одна из актуальных задач современной механики жидкости и газа. В зависимости от процессов, определяющих рост неоднородностей, для свободного сферического пламени различают гидродинамическую (Дарье-Ландау), термодиффузионную и неустойчивость Рэлея-Тейлора. Условиям для развития последней и посвящена данная работа.
Неустойчивость Рэлея-Тейлора возникает на границе раздела двух жидкостей или газов разной плотности при наличии ускорения, направленного от более легкого к тяжелому. При распространении пламени менее плотные разогретые продукты горения двигаются с ускорением в более плотном газе. Когда вектор ускорения и градиент плотности на фронте пламени сонаправлены, происходит развитие неустойчивости. Основным параметром, определяющим скорость развития этой неустойчивости, является число Атвуда. В ходе работы было рассчитано число Атвуда и обнаружено, что на границе раздела продуктов сгорания и горючей смеси оно зависит от начального содержания водорода.
Для исследования развития неустойчивостей была проведена серия экспериментов. Прозрачные латексные оболочки наполнялись предварительно подготовленной водородно-воздушной смесью. В различных сериях экспериментов менялось процентное содержание водорода. Инициирование пламени производилось искровым разрядом с энергией 1мДж, разрядником, расположенным в центре оболочки. Регистрация распространения фронта пламени производилось с использованием теневого метода реализованного в теневом приборе ИАБ-451 и высокоскоростной камеры ВидеоСпринт. Видеосъемка процесса производилась с частотой от 500 до 1000 кадров в секунду с экспозицией в 500 мкс. С целью автоматизации обработки полученных изображений в среде Matlab написана программа, преобразовывающая набор изображений расширяющегося фронта пламени в зависимость среднего радиуса от времени.
Обнаружено, что на начальной стадии распространения возникают как ускорения, так и замедления фронта пламени. Экспериментально полученные параметры распространения фронта пламени дополнены расчетами, проведенными по аналитической модели из литературы.
Работа выполнена при поддержке Российского Научного Фонда, грант №14-50-00124.
Артём Евгеньевич Ельянов