Математическое моделирование задачи искрового зажигания аэровзвеси алюминия
Томский государственный университет
В настоящей работе численно решена задача искрового зажигания аэровзвеси порошка алюминия. Целью работы являлось определение критических условий зажигания порошка алюминия в зависимости от размера и массовой концентрации частиц. Постановка задачи основана на физико-математических постановках [1 – 2].
Математическая постановка задачи определяется системой уравнений, записанной в цилиндрической системе координат, и состоящей из уравнений неразрывности для газа, сохранения импульса и энергии для газа и частиц, баланса массы кислорода и частиц в смеси, уравнений счетной концентрации частиц и состояния газа. В уравнениях, определяющих математическую постановку задачи, правые части, отвечающие за химическое взаимодействие газа и частиц, определяются через радиус алюминия в частице, слагаемые, определяющие инерционное и тепловое взаимодействие определяются через радиус самой частицы, состоящей из алюминия и оксидного слоя. Радиус частицы и радиуса алюминия, оставшегося в частице после выгорания, определялись согласно [2].
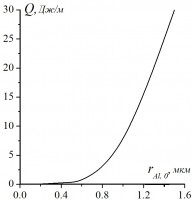
Задача решалась численно с использованием методов [3 – 4]. Метод решения и выбор расчетной сетки соответствовали работе [1]. В расчетах варьировались начальный радиус частиц алюминия и начальная массовая концентрация порошка на единицу объема. Из расчетов определялась минимальная энергия искры, необходимая для зажигания и дальнейшего распространения фронта горения по аэровзвеси. Пример полученных результатов расчета представлен на рис. 1.
На рис. 1 представлена зависимость минимальной энергии искрового зажигания от начального размера частицы алюминия. Видно, что для радиуса частицы меньше 0.5 мкм минимальная энергия искрового зажигания стремится к одному и тому же значению.
В работе было выполнено исследование влияния массовой концентрации порошка на минимальную энергию искрового зажигания аэровзвеси алюминия. Получено, что увеличение массовой концентрации порошка приводит к уменьшению минимальной энергии искрового зажигания.
Исследование выполнено за счет гранта Российского научного фонда (проект №17-79-20011).
1.Моисеева К. М., Крайнов А. Ю. Численное моделирование искрового зажигания аэровзвеси угольной пыли// Физика горения и взрыва. 2018. Т. 54. № 2. С. 61–70.
2.Порязов В.А., Крайнов А.Ю., Крайнов Д.А. Математическое моделирование горения пороха Н с добавлением порошка алюминия// Инженерно-физический журнал. 2015. Т. 88. № 1. С. 93-101.
3.Годунов С.К., Забродин А.В., Иванов М.Я., Крайко А.Н., Прокопов Г.П. Численное решение многомерных задач газовой динамики. – М.: Наука, 1976.
4.Крайко А.Н. О поверхностях разрыва в среде, лишенной ‘собственного' давления// Прикладная математика и механика. 1979. Т. 43. № 3. С. 500-510.