Санкт-Петербургский политехнический университет Петра Великого
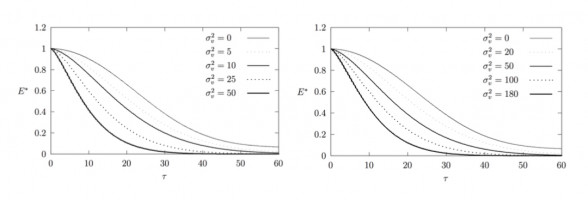
Рассматривается процесс перехода механической энергии в тепловую в нанокристалле без дефектов. Взаимодействие между частицами кристалла – нелинейное, учитывается влияние только ближайших соседей. Начальная температура кристалла задаётся случайными скоростями частиц с нулевым математическим ожиданием и равномерным распределением. Механическая энергия кристалла определяется энергией заданной на нём гармонической волны, после чего численно решается задача Коши для ячейки периодичности с последующим усреднением результатов по ансамблю реализаций [1].
Введение в модель идеального кристалла тепловых скоростей частиц приводит к необратимости распределения энергии волны между частицами, если тепловая энергия кристалла достаточно велика в сравнении с механической энергией [2]. В данной работе для реальных кристаллов показывается необратимость этого перехода, а также сохранение волной её первоначальной формы при уменьшающейся амплитуде. Убывание механической энергии со временем описывается модифицированным экспоненциальным законом, что позволяет определить коэффициент внутреннего трения кристалла и описать движение частиц с помощью уравнения продольных колебаний стрежня.
Результаты работы были получены с использованием вычислительных ресурсов суперкомпьютерного центра Санкт-Петербургского политехнического университета Петра Великого.
1. A. M. Krivtsov. Energy distribution in one-dimensional crystal. Dokl. Phys. 60 (9), page 407, 2015.
2. D. V. Tsvetkov, A. M. Krivtsov. Energy distribution in one-dimensional crystal. Proc. of XXIV ICTAM, pp. 2450-2451.
Егор Борисович Старобинский
НИИ механики МГУ им. М.В. Ломоносова
В докладе излагается методика применения конечно-разностной реализации численной схемы из семейства WENO (weighted essentially non-oscillating, [1]) для моделирования нестационарных течений совершенного газа с ударными волнами. Методы этого класса позволяют достичь произвольно высокого порядка аппроксимации решения и тем самым существенно сэкономить вычислительные ресурсы. Дополнительным достоинством этих методов (отраженном в их названии) является практически полное отсутствие осцилляций параметров решения вблизи газодинамических разрывов – ударных волн и контактных разрывов.
Описывается реализация разновидности метода WENO-Z [2] 5 порядка аппроксимации для моделирования плоских и осесимметричных двумерных, а также трехмерных течений совершенного газа в рамках уравнений Эйлера. Реализация включает в себя Roe-осреднение параметров газа между узлами сетки, характеристическую декомпозицию векторов состояния и потоков газа, а также процедуру H-коррекции для подавления формирования «карбункулов» на фронтах ударных волн [3].
Работа выполнена в НИИ механики МГУ им. М.В. Ломоносова с использованием ресурсов суперкомпьютерного комплекса МГУ им. М.В. Ломоносова при частичной поддержке Российского фонда фундаментальных исследований (грант №18-01-00793) и Министерства образования и науки РФ (договор №14.G39.31.0001 от 13.02.2017г.).
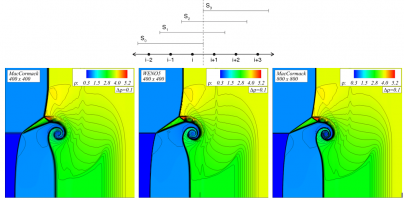
(подпись к рисунку 1) Разностный шаблон WENO, используемый для вычисления потоков газодинамических величин между расчетными узлами. Шеститочечный шаблон (схема 5 порядка точности) состоит из нескольких соседних трехточечных шаблонов, каждому из которых присваивается свой вес в суммарной аппроксимации потока.
(подпись к рисунку 2) Сравнение расчетов двумерной задачи Римана о распаде газодинамического разрыва методами Маккормака (TVD-модификация, 2-й порядок аппроксимации) и WENO (5-й порядок): поле плотности. На одной и той же сетке в 400х400 узлов метод WENO (посередине) дает существенно более точное разрешение элементов течения – ударных волн, тангенциальных разрывов и вихрей, чем метод Маккормака (слева). Примерно такое же разрешение достигается методом Маккормака на вдвое более подробной сетке (справа).
1. G.S.Jiang, C.W. Shu Efficient implementation of weighted ENO schemes // Journal of computational physics. 1996. V. 126. №. 1. P. 202-228.
2. M. Castro, B. Costa, W.S. Don High order weighted essentially non-oscillatory WENO-Z schemes for hyperbolic conservation laws // Journal of Computational Physics. 2011. V. 230. №. 5. P. 1766-1792.
3. R. Sanders, E. Morano, M.C. Druguet Multidimensional dissipation for upwind schemes: stability and applications to gas dynamics // Journal of Computational Physics. 1998. V. 145. №. 2. P. 511-537.
Олег Георгиевич Сутырин
Уральский государственный университет путей сообщения
Рассмотрена полная система уравнений Навье-Стокса в случае одномерного плоско-симметричного течения вязкого теплопроводного сжимаемого газа, с независимыми термодинамическими параметрами δ=1/ρ – удельный объем, p – давление [1, 2]. Для неё поставлена начально-краевая задача c условием непротекания на границах x=0 и x=π и условием теплоизоляции на этих же границах.
Решение данной начально-краевой задачи представляется в виде бесконечных тригонометрических рядов. Чтобы получить уравнения для коэффициентов рядов, каждое уравнение системы проецируется на свою систему базисных гармоник. Из-за того, что эти коэффициенты зависят только от одной переменной, данной процедурой задача построения всего решения сводиться к решению бесконечной системы обыкновенных дифференциальных уравнений (СОДУ).
Чтобы численно построить решение полученной СОДУ, ограничиваем количество слагаемых рядов, а также упрощаем выражения в правых частях СОДУ, избавившись от двойных сумм. Данная СОДУ решается с помощью метода Рунге-Кутты 4-го порядка точности. После нахождения коэффициентов рядов, их значения подставляются в исходное представление решения.
Полученное решение полной системы уравнений Навье-Стокса совпадает с результатами предыдущих исследованиях полученными в [1].
1.Баутин С.П., Замыслов В.Е., Скачков П.П. Математическое моделирование тригонометрическими рядами одномерных течений вязкого теплопроводного газа. Новосибирск: Наука; Екатеринбург: Изд-во УрГУПС, 2014.
2.Баутин С.П. Характеристическая задача Коши и её приложения в газовой динамике. Новосибирск: Наука, 2009.
Екатерина Анатольевна Родина
Уральский Государственный Университет Путей Сообщения
Тропический циклон — тип циклона, или погодной системы низкого давления, что возникает над теплой водяной поверхностью и сопровождается мощными грозами, выпадением ливневых осадков и ветрами штормовой силы. Традиционно считается, что тропические циклоны получают энергию от поднятия влажного воздуха вверх, конденсации водяных паров в виде дождей и опускания более сухого воздуха вниз.
В книгах [1,2] предложена другая схема возникновения и функционирования тропических циклонов. Неравномерный локальный нагрев подстилающей поверхности приводит к появлению неоднородностей температуры, плотности и давления. При действии сил тяжести и Кориолиса это является причиной возникновения сложного нестационарного закрученного движения среды.
Для решения задачи о моделировании трехмерных нестационарных течений, имеющих место в тропических циклонах, предлагается строить решение полной системы дифференциальных уравнений Навье-Стокса, при действии сил тяжести и Кориолиса. Для численного моделирования таких течений используется метод конечных разностей с использованием явной разностной схемы.
1.Баутин С.П. Торнадо и сила Кориолиса. Новосибирск: Наука, 2008.
2.Баутин С.П., Дерябин С.Л., Крутова И.Ю., Обухов А.Г. Разрушительные атмосферные вихри и вращение Земли вокруг своей оси. Екатеринбург: Изд-во УрГУПС, 2017.
Юлия Анатольевна Агеева