Численное моделирование одномерного течения вязкого теплопроводного газа с помощью тригонометрических рядов

Автор: Екатерина Анатольевна Родина

Соавторы: Баутин Сергей Петрович

Организация: Уральский государственный университет путей сообщения

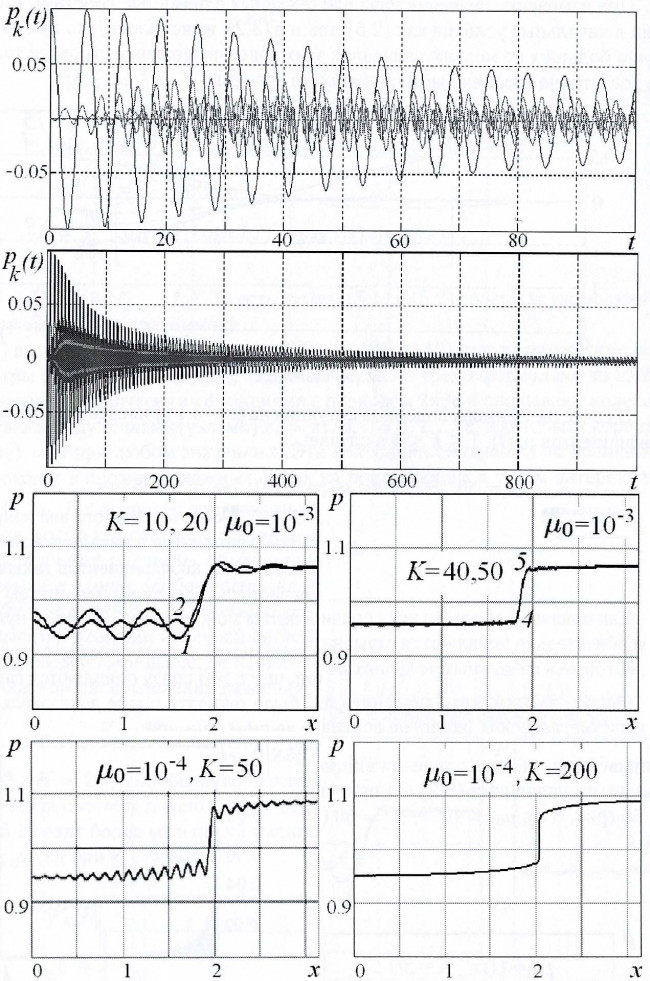
Рассмотрена полная система уравнений Навье-Стокса в случае одномерного плоско-симметричного течения вязкого теплопроводного сжимаемого газа, с независимыми термодинамическими параметрами δ=1/ρ – удельный объем, p – давление [1, 2]. Для неё поставлена начально-краевая задача c условием непротекания на границах x=0 и x=π и условием теплоизоляции на этих же границах.

Решение данной начально-краевой задачи представляется в виде бесконечных тригонометрических рядов. Чтобы получить уравнения для коэффициентов рядов, каждое уравнение системы проецируется на свою систему базисных гармоник. Из-за того, что эти коэффициенты зависят только от одной переменной, данной процедурой задача построения всего решения сводиться к решению бесконечной системы обыкновенных дифференциальных уравнений (СОДУ).

Чтобы численно построить решение полученной СОДУ, ограничиваем количество слагаемых рядов, а также упрощаем выражения в правых частях СОДУ, избавившись от двойных сумм. Данная СОДУ решается с помощью метода Рунге-Кутты 4-го порядка точности. После нахождения коэффициентов рядов, их значения подставляются в исходное представление решения.

Полученное решение полной системы уравнений Навье-Стокса совпадает с результатами предыдущих исследованиях полученными в [1].

1.Баутин С.П., Замыслов В.Е., Скачков П.П. Математическое моделирование тригонометрическими рядами одномерных течений вязкого теплопроводного газа. Новосибирск: Наука; Екатеринбург: Изд-во УрГУПС, 2014.

2.Баутин С.П. Характеристическая задача Коши и её приложения в газовой динамике. Новосибирск: Наука, 2009.