Экспериментальное исследование течения пены с локальным препятствием
Автор: Наталья Дмитриевна Шмакова
Соавторы: Е.В. Ерманюк, С.Ф.А. Сантуччи
Организация: Институт гидродинамики им. М.А. Лаврентьева СО РАН
В повседневной жизни мы часто используем материалы, относящиеся к так называемой «мягкой материи» (soft matter). Так, например, шоколадный мусс, пена для бритья или строительная пена являются представителями широкого класса материалов с многомасштабной двухфазной структурой (газовые пузырьки в жидкой фазе) и имеют двойственное механическое поведение: твердые вещества в состоянии покоя, и жидкости, при воздействии напряжений, превышающих некоторый критический уровень. Такие специфические реологические свойства позволяют использовать пены в различных областях применения, от продуктов пищевой, косметической и фармацевтической промышленности до крупномасштабных промышленных процессов в области нефтедобычи и восстановлении почв. Таким образом понимание закономерностей, позволяющих осуществлять контроль течений пен в гетерогенных средах, представляется чрезвычайно важным [1 – 4].
Мы исследуем фундаментальные закономерности течения пен экспериментально в упрощенной модельной постановке. Эксперименты проводятся в ячейке Хеле-Шоу, представляющей собой простейшую модель трещины, образующейся, например, в процессе гидроразрыва пласта.
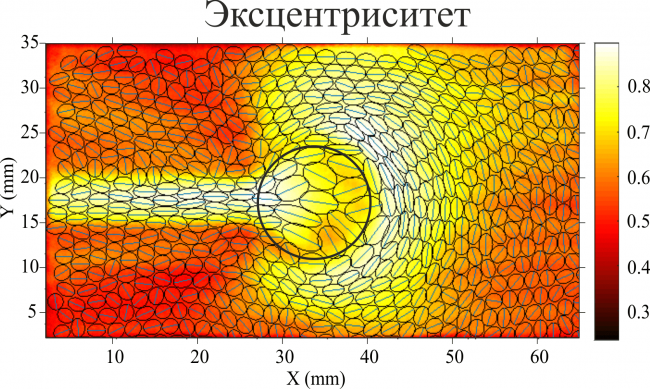
Исследовано течение пены в зависимости от нескольких параметров: величины и формы препятствия, помещенного в ячейку и локально сужающего ее зазор, и количества жидкости в пене. На Рис. 1 показано поле скорости (за вычетом скорости равномерного потока на входе в ячейку, направленного справа налево), демонстрирующее рециркуляцию, характеризующуюся наличием квадрупольного возмущения, а также ускорение пены вниз по течению от препятствия, что напоминает т.н. эффект «отрицательного следа» в течении за всплывающими воздушными пузырьками в вязкоупругих жидкостях [5].
Анализ экспериментальных данных показал, что интенсивность рециркуляционных течений зависит как от высоты препятствия, так и от свойств самой пены (сухая – жидкая): скорость потока вниз по течению от препятствия выше для сухой пены. Также было показано влияние горизонтального размера препятствия и его формы: в зазоре над квадратным препятствием возникают дополнительные особенности в виде вихрей на углах [6].
Работа выполнена при поддержке гранта МОН РФ № 14.W03.31.0002
1. Weaire D., Hutzler S. The Physics of Foams // Oxford University Press, 1999
2. Cantat I., Cohen-Addad S., Elias F., Graner F., Hohler R., Pitois O., Rouyer F. and Saint-Jalmes A. Foams, Structure and Dynamics // Oxford University Press, 2013
3. Dollet B., Graner F. Two-dimensional flow of foam around a circular obstacle: Local measurements of elasticity, plasticity and flow // J. Fluid Mech., 2007, V. 585 P. 181
4. Stevenson P. Foam Engineering: Fundamentals and Applications // Wiley, 2012
5. Hassager O. Negative wake behind bubbles in non-newtonian fluids // Nature, 1979, V. 279 P. 402
6. Chevalier, T., J. Koivisto, N. Shmakova, Alava M.J., Puisto A., Raufaste C., Santucci S. Foam flows through a local constriction //J. Phys. Conf. Ser., 2017, V. 925, P. 012025.


