Гиперзвуковые течения. Режим сильного вязко-невязкого взаимодействия
Автор: Георгий Николаевич Дудин
Организация: ФГУП "ЦАГИ"
В первой части лекции, которая носит обзорный характер, приведены результаты исследований гиперзвуковых течений вязкого газа начиная с середины XX века. Обсуждаются особенности течений для различных режимов вязко-невязкого взаимодействия, которые были установлены в экспериментальных работах Борового В.Я., Майкапара Г.И., Whitehead A.H., Hefner J.N., Rao D.M., Cross E.J. и др. Для режима сильного взаимодействия приведены автомодельные решения: Lees L.J. – Stewartson K. - обтекания полубесконечной пластины, Whalen R.J. - скользящей пластины и Ладыженского М.Д. - плоских треугольных крыльев. Далее обсуждаются вопросы, связанные с распространением возмущений против потока, которое впервые в 1970 году было установлено Нейландом В.Я. [1, 2]. Приведены результаты исследований Stewartson K. обтекания пластины с учетом решения уравнений для ударного слоя, а также решения Михайлова В.В., Нейланда В.Я., Дудина Г.Н. для обтекания треугольных крыльев на режиме сильного взаимодействия.
Во второй части лекции обсуждается вопрос о возможности образования пространственного течения на пластине конечной длины на режиме сильного взаимодействия. В предположении, что на задней кромке пластины задается дополнительное условие, которое является функцией от поперечной координаты и, учитывая вид первых членов разложения для функций течения в окрестности передней кромки [3], сформулированы и решены краевые задачи для определения следующих членов разложения. Впервые показано, что для функций течения p(x, z), δ(x, z), u(x, Y, z), ν(x, Y, z), H(x, Y, z) эти члены имеют порядок O( (pα(z)/p0)2 x2α), а для w(x, Y, z) - O( dpα(z)/dz (pα(z)/(p0)2) x2α+1), где α - собственное число и pα(z) - произвольный параметр. Установлено, что возникающее вторичное течение в сечениях пропорционально величине dpα(z)/dz.
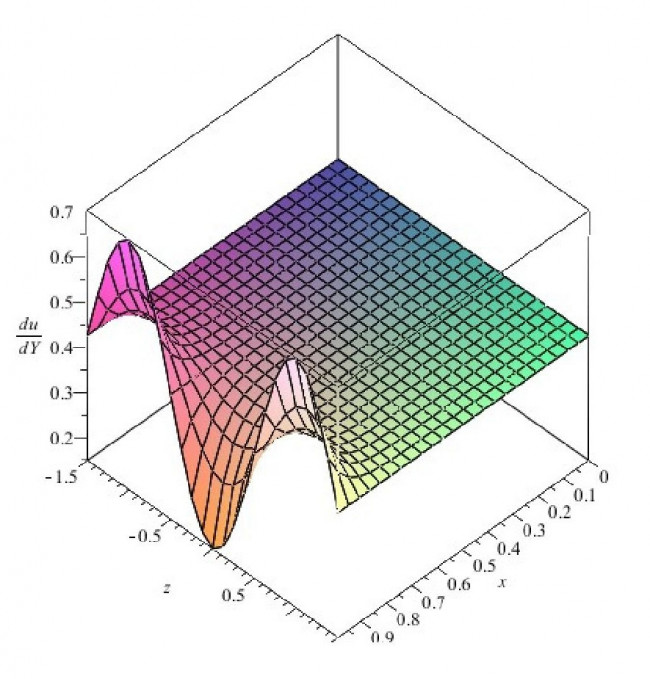
На рисунке приведена зависимость du/dY на поверхности пластины, которая пропорциональна коэффициенту продольного трения, при температурном факторе Hw=1.5 и параметре pα(z)=0.2 cos(πz).
Рассмотрено также обтекание скользящей пластины. Установлено принципиальное отличие от предыдущего случая. Уравнение для w(x, Y, z) не отделяются от основной системы уравнений, а самое главное, третьи члены разложений имеют порядок O( (dpα(z)/dz) xα+1). Таким образом, при наличии угла скольжения, влияние третьего члена разложения на распространений возмущений существенно больше, чем при отсутствии скольжения. Установлено, что увеличение угла скольжения приводит к значительному уменьшению значений собственного числа.
Работа выполнена при финансовой поддержке РФФИ (проект № 18-01-00211).
1. Нейланд В.Я. Распространение возмущений вверх по течению при взаимодействии гиперзвукового потока с пограничным слоем // Изв. АН СССР. МЖГ. 1970. № 3. С. 40-49.
2. Нейланд В.Я., Боголепов В.В., Дудин Г.Н., Липатов И.И. Асимптотическая теория сверхзвуковых течений вязкого газа. – М.: Физматлит, 2003. – 456 с.
3. Дудин Г.Н., Нейланд В.Я. Об индуцировании трехмерных возмущений в пограничном слое при сильном взаимодействии с гиперзвуковым потоком // Изв. РАН. МЖГ. 2018. № 1. С. 89-96.


