Истечение идеального газа из цилиндрического или сферического источника в пустоту

Автор: Харис Фаритович Валиев

Соавторы: -

Организация: ЦИАМ им. П.И. Баранова

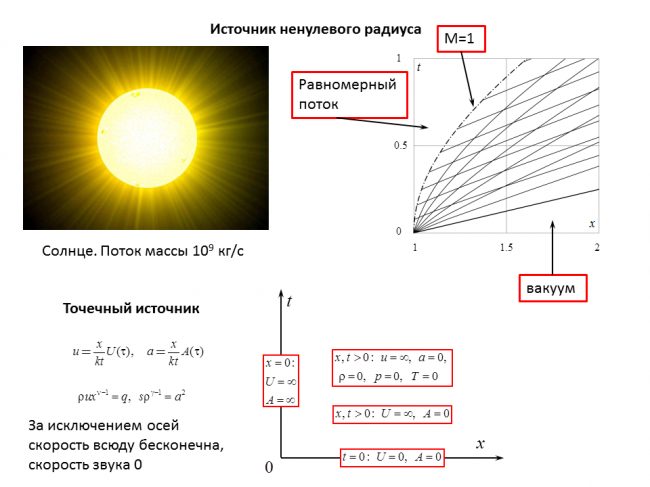
Получены решения начально-краевых задач об истечении идеального (невязкого и нетеплопроводного) совершенного газа из цилиндрических или сферических источников в пустоту. Время отсчитывается от момента включения источника, вне которого в момент включения – пустота. Фиксируются энтропийная функция, расход ("интенсивность" источника), равное или большее единицы начальное число Маха истекающего из источника газа, а также радиус начального цилиндра или сферы ("радиус источника"). Если радиус источника больше нуля, то область течения в плоскости "радиальная координата - время" состоит из двух подобластей: подобласти стационарного течения от источника и примыкающей к ней неавтомодельной центрированной волны разрежения (ЦВР) из С^–-характеристик. Стационарное течение описывается известными конечными формулами, а ЦВР рассчитывается методом характеристик для одномерных нестационарных течений. При больших значениях радиальной координаты расчеты методом характеристик подтвердили полученные ранее асимптотические закономерности.

Граница между ЦВР и пустотой – прямая С⁰-характеристика (траектория частиц), совпадающая с граничной и единственной прямолинейной С^–-характеристикой ЦВР. Она же – асимптота части С⁺-характеристик. Течение, возникающее при истечении в пустоту из источника с нулевым начальным радиусом, т.е. из "точечного" источника, принципиально отличается от описанного выше. В рассмотренной постановке при заданном конечном расходе и нулевом радиусе такого источника начальные скорость, плотность и скорость звука газа, истекающего из него, бесконечны. Вне зависимости от величины радиуса источника скорость газа и в стационарной части течения, и в нестационарной ЦВР с ростом радиальной координаты растет, а плотность и скорость звука уменьшаются. Показано, что такое же поведение этих параметров будет и для точечного источника. При этом скорость газа, будучи изначально бесконечной, остается такой всюду, а плотность и скорость звука, уменьшаясь, становятся нулевыми при любых ненулевых значениях радиальной координаты. При нулевом радиусе источника рассматриваемая задача становится автомодельной. Ее решение в плоскости "автомодельных" скорости и скорости звука дается тремя особыми точками дифференциального уравнения с этими переменными. Согласно сказанному выше в одной из них автомодельная скорость бесконечна, а автомодельная скорость звука равна нулю.

Работа выполнена при поддержке Российского фонда фундаментальных исследований (№ 17-01-00126).

Х.Ф. Валиев, А.Н. Крайко. Истечение идеального газа из цилиндрического или сферического источника в пустоту // Изв. РАН.Механика жидкости и газа. 2018. №5.