К ЧИСЛЕННОМУ ИНТЕГРИРОВАНИЮ УРАВНЕНИЙ НЕЛИНЕЙНОЙ АКУСТИКИ ПРИМЕНИТЕЛЬНО К ЗВУКОВОМУ УДАРУ
Автор: Харис Фаритович Валиев
Соавторы: А.Н. Крайко, Е.А. Яковлев
Организация: ЦИАМ им. П.И. Баранова
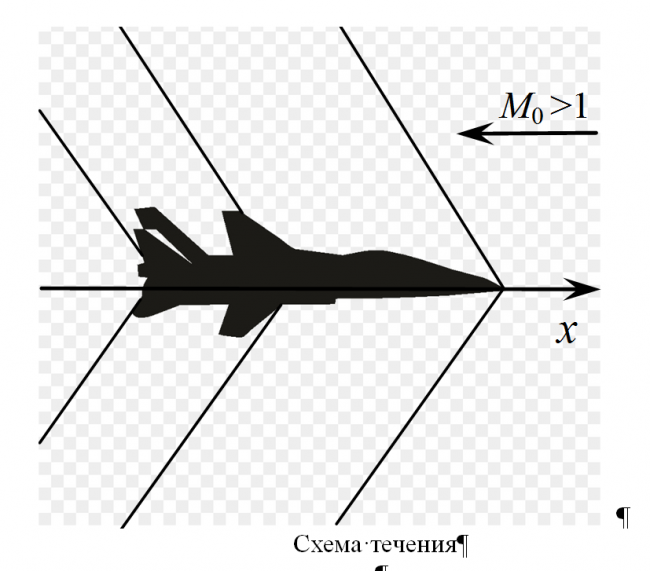
Огромное многообразие работ по математическому моделированию звукового удара, возникающего при полёте сверхзвуковых гражданских самолетов, предполагает разбиение всего течения на две подобласти: близкую к летательному аппарату (ЛА) и далекую от него. В близкой подобласти возмущения течения велики, а скачки уплотнения (ударные волны - УВ) интенсивны и имеют сложную пространственную структуру. В системе координат ЛА течение в этой подобласти в основном стационарное и сверхзвуковое с небольшими дозвуковыми зонами, в частности, вблизи затупленных кромок крыльев. Влияние нестационарности вихрей, сходящих с концов крыльев и хвостового оперения, реактивных струй и турбулентности в пограничных слоях на эволюцию ударно-волновых структур, ответственных за звуковой удар, невелико и убывает с удалением от ЛА. Поэтому для моделирования звукового удара расчет течения в ближней подобласти возможен в рамках уравнений Эйлера. По сравнению с современными расчетами обтекания всего ЛА в приближении осредненных по Рейнольдсу уравнениями Навье-Стокса (RANS) такой расчет много проще, ибо не требует сгущения сетки у поверхностей, обтекаемых без прилипания, и пограничных слоев. Существенно то, что установлением по времени нужно рассчитывать область, ограниченную длиной ЛА, а далее вести счет маршем по оси х, направленной по скорости набегающего на ЛА сверхзвукового потока. Чтобы правильно рассчитать эволюцию ударно-волновой структуры, при маршевом счете следует при каждом х ограничиваться только возмущенной областью, по возможности адаптируя сетку к зоне УВ. При удалении по х от ЛА на 5-10 его длин, когда максимальное относительное возмущение давления |Dp/p0| уменьшится до 0.1, следует переходить к маршевому счету [1] в приближении нелинейной акустики. Явное выделение в этом приближении "внешней" и "внутренней" близких к коническим, "бегущих в одном направлении" слабых УВ при на порядки меньшем, чем вблизи ЛА общем фиксированном числе ячеек позволит рассчитать звуковой удар на расстояния в многие сотни длин ЛА. Ключевой элемент такого расчета - одно семейство сеточных линий, "бегущих в том же направлении" и как следствие - адаптированных к волновой "квазикольцевой" (в дальней подобласти) структуре звукового удара.
Работа выполнена при поддержке РФФИ (20-01-00100 и 18-31-20059).
1.Годунов С.К., Забродин А.В., Иванов М.Я. и др. Численное решение многомерных задач газовой динамики. М.: Наука, 1976. 400 с.
