НИИ механики МГУ, Москва
Графическая аннотация – рисунок, привязанный к каждому докладу на сайте конференции, - важный визуальный элемент, разъясняющий в научно-популярном стиле суть научной работы участника конференции. Из быстрого просмотра графической аннотации на сайте конференции каждый участник нашей конференции, не специализирующийся в данной области механики, должен получить общее представление о содержании доклада. Графическая аннотация должна по возможности ответить по крайней мере на один из следующих вопросов:
- В чем заключается суть предлагаемого метода исследования некоторой научной проблемы? В чем состоит актуальность и научная новизна?
- Какова область практического приложения результатов исследований? Какая выгода от использования результатов исследований?
Если не удается подготовить графическую аннотацию, отвечающую на эти вопросы, то в качестве графической аннотации можно использовать цветной рисунок, иллюстрирующий
- результаты расчётов, излагаемых в докладе;
- постановку эксперимента;
- схему исследуемого физического явления;
- другой иллюстративный материал, который будет излагаться в докладе.
Графическая аннотация должна быть рисунком в формате JPEG или PNG, размер которого не превышает 0.5 Мб.
С графическими аннотациями конференций 2017 и 2018 годов можно ознакомиться на сайте нашей конференции.
Оргкомитет
НИИ механики МГУ, Москва
Каждому участнику конференции предоставляется возможность сделать не более одного устного доклада и 1-2 стендовых доклада. На устном докладе участник представляет основное содержание своей работы. Ожидается, что изложение устного доклада даётся в научно-популярном стиле, понятном для широкой аудитории. На стендовых докладах, дополняющих устный доклад, участник делает сообщение о частных узкоспециализированных проблемах и результатах. Продолжительность устных докладов будет определяться исходя из числа участников (но не более 20 минут). Участнику необходимо направить в адрес Оргкомитета отдельную аннотацию для каждого доклада (и устного, и стендовых).
Оргкомитет
НИИ механики МГУ
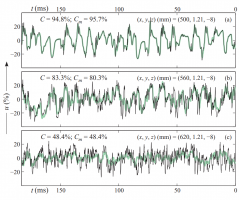
Известно, что поверхность, обтекаемая высокоскоростным потоком, разогревается до температуры близкой к локальной температуре торможения невозмущенного потока. Однако полного восстановления температуры до значения температуры торможения не происходит. Если поверхность теплоизолирована (непроницаема для теплового потока), то ее температура (адиабатная температура стенки) будет равна температуре пристенного слоя газа, в общем случае не равной температуре торможения потока.
Во многих прикладных задачах (теплозащита, безмашинное энергоразделение и т.п.) снижение адиабатной температуры стенки относительно температуры торможения приводит к существенному повышению положительного эффекта [1]. Решение данной задачи возможно через использование свойств газокапельных потоков с малой массовой концентрацией (до процента) жидкой фазы. В этом случае жидкая фаза практически не влияет на свойства основного газового потока, при этом сами капли могут охлаждаться до термодинамической температуры потока.
В работе представлены результаты измерения температуры поверхности плоской пластины, обтекаемой сверхзвуковым воздушным и воздушно-капельным потоком. Экспериментальные исследования проводились на сверхзвуковом аэродинамическом стенде с использованием систем регистрации данных National Instruments, автоматизированных программ опроса и обработки показаний сенсорных устройств в среде LabView, термопар с термокомпенсацией, зондовых измерений, тепловизионных и оптических методов визуализации картины течения [2].
Металлическая пластина устанавливалась вертикально в рабочем канале аэродинамической установки. Капли жидкости (дистиллированная вода) в воздушный поток распылялись в форкамере через центробежные форсунки. Массовая концентрация жидкости составляла до 0.5% расхода воздуха, средний диаметр капель по Заутеру – 110 мкм, число Маха набегающего потока М = 2.5, 3.0. Результаты измерений температуры поверхности пластины для случая однофазного (без капель) воздушного потока сравнивались с результатами для воздушно-капельного потока при одинаковых параметрах (по воздуху) в форкамере.
1. Leontiev A.I., Popovich S.S., Vinogradov U.A., Strongin M.M. Experimental research of supersonic aerodynamic cooling effect and its application for energy separation efficiency // Proceedings of the 16th International Heat Transfer Conference, IHTC-16. 2018. V. 212244. 8 p.
2. Попович С.С., Здитовец А.Г, Киселев Н.А., Виноградов Ю.А., Медвецкая Н.В. Измерение адиабатной температуры стенки плоской пластины, обтекаемой сверхзвуковым воздушно-капельным потоком // Известия Российской академии наук. Механика жидкости и газа. 2020. № 5.
Сергей Станиславович Попович
ИОРАН, Москва
На рисунке: Типичная картина волновой турбулентности после каскада неустойчивостей волнового аттрактора (пунктирная линия).
Гравитационно-инерционные волны играют существенную роль в формировании абиссального профиля плотности океана и могут переносить порядка 1 Тв энергии от глобальных баротропных приливов к мелкомасштабным [1]. За исключением отдельных конфигураций топографии дна и характеристик профилей солености и температуры, глубинное волновое движение является турбулентным или стохастическим. В последние годы активно развиваются исследования аккумуляции волновой энергии за счет фокусировки волн на определенных путях вследствие специфического закона отражения от наклонных поверхностей. В общем случае в стратифицированной жидкости, заполняющей область с наклонными границами, формируется волновой аттрактор, ширина которого определяется вязкостью. При этом средняя кинетическая энергия может возрасти в десятки раз. Ламинарный волновой аттрактор виден невооруженным взглядом как в экспериментах, так и при численном моделировании [2-4. Этого нельзя сказать про турбулентные режимы, возникающие из волновых аттракторов после каскада неустойчивостей. Здесь волновой аттрактор на первый взгляд не проявляется, а во всей области наблюдается турбулентное движение, характерные масштабы которого могут изменяться. Однако наше исследование показало, что особенно в областях с большим аспектным соотношением, турбулентные режиме даже после каскада неустойчивостей продолжают насыщаться от линейного механизма фокусировки пучков волн. Причем конечный спектр турбулентного движения сильно отличается в областях с малым, и с большим аспектным соотношением: в случае малого аспектного соотношения доминирует каскад триадных субгармонических неустойчивостей [4], в то время как для большого аспектного соотношения доминирует супергармонические частоты, кратные целой и половинной частотам внешнего воздействия. Данные результат важен для анализа спектров волновой турбулентности в различных областях мирового океана.
1. Garrett, C. & Kunze, E. 2007 Internal tide generation in deep ocean. Annu. Rev. Fluid Mech. 39, 57–87.
2. И. Н. Сибгатуллин and Е. В. Ерманюк. Аттракторы внутренних и инерционных волн (обзор). Прикладная механика и техническая физика, (2):113–136, 2019.
3. Ilias Sibgatullin, Evgeny Ermanyuk, Leo Maas, Xu Xiulin, and Thierry Dauxois. Direct numerical simulation of three-dimensional inertial wave attractors. IEEE Conference Proceedings, page 17526262, 2017.
4. C. Brouzet, I. N. Sibgatullin, H. Scolan, E. V. Ermanyuk, and T. Dauxois. Internal wave attractors examined using laboratory experiments and 3d numerical simulations. Journal of Fluid Mechanics,
Ильяс Наилевич Сибгатуллин
Математический институт им. В.А. Стеклова Российской академии наук, Москва
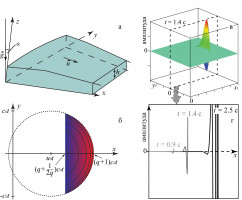
Течения потоков жидкости по наклонным поверхностям часто встречаются в природе и различных технических приложениях. С первой четверти XX века устойчивость таких потоков и развитие возмущений в них активно изучались аналитически, экспериментально, а позже и численно (см., например, [1, 2]). В настоящей работе аналитически в линейном приближении с помощью метода перевала изучается асимптотическое поведение локализованного по пространству и времени возмущения слоя линейно-вязкой жидкости на наклонной плоскости. Течение описывается уравнениями в гидравлическом приближении, то есть осреднёнными по глубине уравнениями МСС с учётом некоторых предположений (см., например, [3]). Рассматривается однородный неустойчивый поток на склоне постоянного уклона α (рис. 1а). Ранее эволюция трёхмерного локализованного возмущения открытого потока на вертикальной стенке исследовалась методом перевала в работах [2, 4]. В [2] (Глава 11, с. 327) рассматривалось течение, описываемое обобщённым уравнением Курамото-Сивашинского; в [4] — течение, описываемое системой уравнений Капицы-Шкадова.
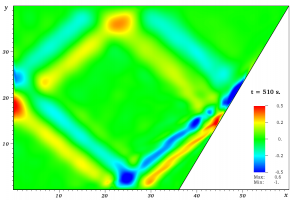
Локализованное возмущение представляется суммой двойных интегралов Фурье, где интегрирование ведётся по всем вещественным волновым числам kx, ky (kx, ky — компоненты волнового вектора), суммирование — по корням дисперсионного уравнения (см. [5]). В начальный момент времени возмущение задаётся дельта-функцией. С помощью метода перевала определены размеры и форма области пространства, занятой растущим возмущением (рис. 1б), и поведение волны внутри этой области. (Обозначения: g — ускорение свободного падения, h — глубина потока, q = u0/c0, c0 = (gh0cosα)1/2, u0 — скорость невозмущённого потока, направленная вдоль оси x, нижний индекс «0» отмечает величины, относящиеся к невозмущённому течению.) Возмущение растёт внутри сегмента круга радиуса c0t с центром в точке x = u0t, y = 0. Гребни растущих волн — дуги окружностей с центром в той же точке (показаны серым на рис. 1б). Длина волны стремится к нулю при приближении к точке x = (q+1)c0t. Фазовая скорость возмущения превосходит групповую. Визуализация возмущения в пространстве приведена на рис. 1в.
Исследование выполнено за счет гранта Российского научного фонда (проект № 19-71-30012).
1. Алексеенко С.В., Накоряков В.Е., Покусаев Б.Г. Волновое течение пленок жидкости. — Новосибирск: ВО «Наука». Сибирская издательская фирма, 1992. — 256 с.
2. Chang H.-C., Demekhin E.A. Complex Wave Dynamics on Thin Films. D. Möbius and R. Miller. Elsevier. Amsterdam. 2002.
3. Эглит М.Э. Неустановившиеся движения в руслах и на склонах. — М.: Изд-во Моск. ун-та, 1986. — 96 с.
4. Demekhin E.A., Kalaidin E.N., Kalliadasis S., Vlaskin S.Yu. Three-dimensional localized coherent structures of surface turbulence. II. Λ solitons // Phys. Fluids. 2007. V. 19. 114104.
5. Zayko J., Eglit M. Stability of Downslope Flows to Two-Dimensional Perturbations. // Phys. Fluids. 2019. V. 31. 086601.
Юлия Сергеевна Зайко
МГУ
На рисунке: Вертикальная компонента скорости (слева) и динамика средней кинетической энергии (справа) при бигармоническом воздействии на стратифицированную жидкость.
В мировой океан со стороны солнца и луны постоянно поступает механическая энергия за счет приливного воздействия. Ранее были проведены исследования эффекта аккумуляции кинетической энергии стратифицированной жидкости, возникающих из-за особых свойств дисперсионного соотношения внутренних гравитационных волн при монохроматическом воздействии [1]. Области аккумуляции кинетической энергии характеризуются повышенной скоростью движения жидкости и называются аттракторами. Аттракторы являются распространенным явлением в океане и любых стратифицированных жидкостях [2]. Это явление очевидно оказывает значительное влияние на перемешивание, траекторию движения живых организмов, седиментацию и эрозию поверхностей, с которыми они взаимодействуют. Следует отметить, что появление аттракторов присуще не только стратифицированным жидкостям, но и вращающимся.
Моделирование аттракторов внутренних гравитационных волн на простой геометрии не требует больших вычислительных затрат и позволяет установить характерные режимы течения, оценить потенциал аккумулируемой энергии и проанализировать спектр компонент скорости [3].
В отличии от предыдущих работ, авторами численно получена картина течения стратифицированной жидкости в трапециевидном резервуаре с волнопродуктором воздействующим на жидкость двумя монохроматическими колебаниями (Рис. 1). Проведен анализ результатов прямого численного моделирования бигармонических аттракторов внутренних волн методом спектральных элементов. Исследован спектр вертикальной компоненты скорости, получена его частотно-временная характеристика и средняя кинетическая энергия в резервуаре в зависимости от времени.
1. I. N. Sibgatullin, E. V. Ermanyuk, K. A. Vatutin, D. A. Ryazanov, and X. Xu. Numerical simulation of three-dimensional wave attractors. The XXVII workshop of the Council of nonlinear dynamics of the Russian Academy of Sciences, 47(1):112–115, 2019.
2. Guo, Y., & Holmes-Cerfon, M. (2016). Internal wave attractors over random, small-amplitude topography. Journal of Fluid Mechanics, 787, 148-174. doi:10.1017/jfm.2015.648
3. C. Brouzet, E. V. Ermanyuk, S. Joubaud, I. Sibgatullin, and T. Dauxois. Energy cascade in internal-wave attractors. Europhysics Letters, 113:44001, 2016.
Даниил Александрович Рязанов
Федеральное государственное бюджетное образовательное учреждение высшего образования «Пермский государственный национальный исследовательский университет», Институт механики сплошных сред УрО РАН, Пермь
В настоящей работе экспериментально показана возможность визуализации акустических течений в воде и растворах NaCl. Эксперименты проводились в кювете размерами 110×116×160 мм3, имеющей форму прямоугольного параллелепипеда. Кювета была изготовлена из оргстекла толщиной 3 мм. Электродинамический источник ультразвука находился заподлицо с дном кюветы. Для регистрации динамики пузырьков использовалась высокоскоростная камера. Более подробно методика эксперимента и его специфические особенности описаны в статьях [1, 2]. В качестве рабочих жидкостей использовались: дистиллированная вода, водные солевые растворы NaCl с массовым содержанием соли от 0% до 30%.
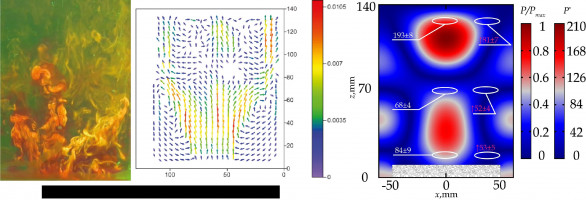
Воздействие горизонтального излучателя УЗ на жидкость сосредоточено в цилиндрическом объёме, в котором выделяют несколько зон в зависимости от расстояния от излучателя. В предварительных экспериментах был использован флюоресцирующий метод визуализации течения. В качестве флюоресцирующего вещества был использован родамин (рис.1, А). Затем, для оценки влияния ультразвукового источника на различные жидкости и растворы был применён метод PIV (Particle Image Velocimetry) - цифровой трассерной визуализации (рис.1, А). Использование данных методов позволило продемонстрировать возможность визуализации акустического течения, а также изучить некоторые его особенности связанные, как показали численные расчеты, с распределением акустического давления в полости ячейки (рис 1, Б). На рис. 1, Б используется две маркерные цветовые шкалы. Первая шкала показывает нормированное на максимальное значение давление, фиксируемое в исследуемой области - P/Pmax. Вторая шкала показывает численное значение среднего значения давления регистрируемого датчиком - P∗. На рисунке 1 наблюдается качественное совпадение течения возникающего в жидкости при визуализации с использованием родамина, PIV, проведённого с использованием метода главных компонент, и численного расчета.
Исследование выполнено за счет гранта Российского научного фонда (проект № 20-69-46066).
1. Козлов М. В., Рыбкин, К. А., Фатталов, О. О., Любимова, Т. П. Динамика парогазовых пузырьков вблизи твердых поверхностей в солевых растворах при дегазации // Теория, эксперимент и новые технологии: конф. (Новосибирск - Шерегеш, 28 февраля-06 марта 2020 г). Новосибирск: Издательство Параллель, 2020. С. 90-91.
2. Rybkin K. A. et al. Experimental study of formation and dynamics of cavitation bubbles and acoustic flows in NaCl, KCl water solutions //Journal of Physics: Conference Series. – IOP Publishing, 2017. – Т. 879. – №. 1. – С. 012026.
Максим Владимирович Козлов
Институт механики сплошных сред УрО РАН
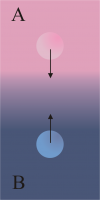
В данной работе экспериментально исследован процесс формирования конвективного течения вследствие неустойчивости двойной диффузии [1, 2] в двухслойной системе смешивающихся жидкостей. Течение представляет собой пальчиковую структуру, распространяющуюся в обе стороны от первоначальной границы контакта слоёв. Эксперименты выполнены в вертикальной ячейке Хеле-Шоу высотой – 9.0 см, шириной – 2.4 см, толщиной – 0.1 см. Изначально система имеет устойчивую стратификацию по плотности (верхний слой легче нижнего), а каждая из жидкостей однородна по концентрации. В исследуемой постановке градиенты концентрации растворенных веществ A и B (также как и градиенты плотности) разнонаправлены, а компоненты диффундируют навстречу друг другу (Рис. 1). В качестве рабочих жидкостей использованы водные растворы ряда неорганических и органических соединений. Варьирование веществ позволило проводить исследование в широком диапазоне управляющих параметров. Для визуализации нестационарного распределения концентрации веществ использован лазерный интерферометр Физо. Для визуализации и оценки интенсивности течения использован метод PIV.
Исследованы три возможные конфигурации системы:
(1) оба вещества имеют положительный знак концентрационной зависимости плотности, т.е. плотность растворителя меньше плотности обоих слоев;
(2) компоненты имеют разные знаки концентрационной зависимости плотности, т.е. плотность растворителя лежит между значениями плотностей обоих слоев;
(3) оба компонента имеют отрицательный знак концентрационной зависимости плотности, т.е. плотность растворителя больше плотности обоих слоев.
Особое внимание сосредоточено на изучении конфигураций 2 и 3, которые ранее в литературе не рассматривались. В докладе обсуждается влияние таких управляющих параметров как соотношение коэффициентов диффузии и коэффициентов концентрационного расширения на тип структуры возникающей конвекции, её интенсивность, а также условия перехода к устойчивости.
Елена Александровна Мошева
НИИ механики МГУ имени М.В. Ломоносова
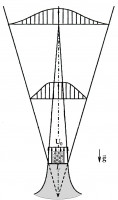
Моделируется течение смеси газа и заряженных частиц, с учётом их взаимодействия и электризации, в случае плоской стационарной затопленной струи несжимаемой жидкости в предположении, что движение частиц не влияет на течение несущей среды. При описании движения частиц используется подход Лагранжа: частицы движутся под действием силы тяжести, гидродинамических и электростатических сил. При взаимодействии (соударении) частиц меняются их скорости и заряды. Предполагается, что смесь состоит из частиц двух различных диаметров. В начальный момент распределение частиц определяется их количеством (или размерами занимаемой ими области), общей концентрацией и долей крупных частиц. Проводится детальное исследование влияния параметров распределения на течение смеси в виде затопленной струи и эволюцию электрического поля в процессе течения. Определяются количественные характеристики электрического поля (накопленный частицами заряд, максимальная напряжённость электрического поля и другие). Оценивается количество и начальная концентрация частиц, при которых напряжённость поля достигает критических значений самостоятельного разряда или молнии.
1. Абрамович Г.Н. Теория турбулентных струй. Репринтное воспроизведение издания 1960 г. М.: ЭКОЛИТ, 2011. 720 с.
2. Горохова Н. В. Эволюция электрического поля в течениях смеси газа с заряженными частицами // XII Всероссийский съезд по фундаментальным проблемам теоретической и прикладной механики: сборник трудов в 4 томах. РИЦ БашГУ Уфа, 2019. Т. 4. С. 31–33.
3. Soo S.L. Dynamics of charged suspensions // International reviews in aerosol physics and chemistry. Vol. 2. Pergamon Press, Oxforf. 1971. P. 61-149.
Наталья Владимировна Горохова
Финансовый университет при Правительстве Российской Федерации
Использование ионоселективных поверхностей для решения проблем микрофлюидики позволило по-новому взглянуть на проблемы транспорта жидкостей в микроканалах. Большой объёмный заряд, который образуется в результате концентрационной поляризации около ионоселективный поверхности, приводит к увеличению электроосмотической скорости в несколько раз. Однако вместе с тем такие течения оказываются менее устойчивыми, по сравнению с электроосмосом около диэлектрической поверхности. Основным механизмом неустойчивости является электрокинетический [1], который в настоящее время активно исследуется. Модель электрокинетической неустойчивости постоянно расширяется для учёта дополнительных эффектов. В недавних работах было показано [2-4], что если отказаться от гипотезы идеальной селективности, то есть допустить наличие потока коионов сквозь поверхность, то можно наблюдать качественно новые режимы электроконвекции, вплоть до колебательного [3,4].
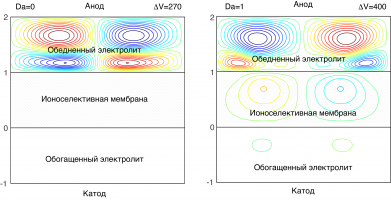
В данном докладе будет представлено следующее обобщение математической модели, которое предполагает наличие гидродинамического течения внутри пористой среды ионообменной мембраны. Для этого в модель было добавлено уравнение Дарси-Бринкмана [5] внутри мембраны. Был проведен линейный анализ устойчивости одномерного стационарного решения, а также двумерное численное моделирование для выявления нелинейных режимов.
Результаты исследования ожидаемо показывали, что движение в жидкости в мембране в большей степени приводит к стабилизации течения, однако увеличение критического значения разности электрических потенциалов происходит немонотонно: с увеличением числа Дарси сначала происходит небольшая дестабилизация, и только для достаточно больших чисел Дарси наблюдается значительная стабилизация.
1. Rubinstein I., Zaltzman B. Electro-osmotically induced convection at a permselective membrane // Phys. Rev. E. 2000. Т. 62. № 2. С. 2238–2251.
2. Rubinstein I., Zaltzman B. Equilibrium Electroconvective Instability // Phys Rev Lett. 2015. Т. 114. № 11. С. 114502–5.
3. Ganchenko G.S. и др. Modes of electrokinetic instability for imperfect electric membranes // Phys. Rev. E. 2016. Т. 94. № 6. С. 063106–8.
4. Demekhin E.A., Ganchenko G.S., Kalaydin E.N. Transition to electrokinetic instability near imperfect charge-selective membranes // Phys Fluids. 2018. Т. 30. № 8. С. 082006–19.
5. Beavers G.S., Joseph D.D. Boundary conditions at a naturally permeable wall // J. Fluid Mech. 2006. Т. 30. № 1. С. 197–207.
Георгий Сергеевич Ганченко
Радиофизический факультет ННГУ имени Н.И. Лобачевского, Н. Новгород
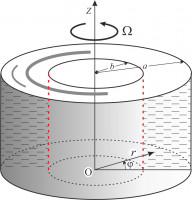
Исследуются основные свойства инерционных (гироскопических) волн во флотирующей вязкой жидкости, образующей центрифугированный слой на твердой стенке цилиндрической полости центрифуги (см. рис.). Наиболее детально рассмотрены азимутальные гироскопические волны. Флотирующая жидкость – это жидкость с инерционной поверхностью, образуемой плавающими на её свободной поверхности и не взаимодействующими между собой частицами, обладающими малой массой. Её движения описываются обычными уравнениями гидродинамики (за исключением того, что в правой части уравнения движения появляются два члена, связанные с действием кориолисовой и центробежной сил, поскольку рассмотрение ведется в неинерциальной системе отсчёта)
(1)
( – динамическая вязкость, – угловая скорость центрифуги, остальные обозначения стандартны), но граничные условия на свободной поверхности являются неклассическими
, ,
где , , , E – число Экмана, – уравнение свободной поверхности, T – вектор, определяющий реакцию частиц инерционной поверхности, в цилиндрической системе координат имеет вид
.
В отличие от традиционного подхода с применением погранслойных функций при решении задач с малым параметром при старших производных, мы ищем не приближенное, а точное решение гидродинамической задачи. Для построения решения используется суперпозиция собственных функций несамосопряженного оператора rot. Собственные вектор-функции v(x) оператора в пространстве соленоидальных полей, определяются из несамосопряженной задачи на собственные значения в двусвязной области. Получено и исследовано дисперсионное уравнение. Показано, инерционная поверхность оказывает дестабилизирующее действие. Получены оценки параметров, при которых стационарное движение жидкости является устойчивым.
Мария Андреевна Свешникова
МГУ имени М.В. Ломоносова
Гидравлическим прыжком называется резкое изменение толщины слоя жидкости, текущего по твердой поверхности, данное явление соответствует ударной волне при аналогии между течениями тонкого слоя и газовой динамикой. В настоящей работе рассматриваются круговые гидравлические прыжки, которые возникают при растекании вязкой жидкости по горизонтальному диску в радиальном направлении; струя жидкости падает в центр диска с постоянным расходом.
Рассматривается задача об определении положения гидравлического прыжка в случае, когда горизонтальная поверхность вращается. Положение прыжка определяется балансом сил инерции, трения и гидростатического давления, вращение передает дополнительные импульс жидкости за счет центробежной силы и силы Кориолиса.
Теоретическое исследование ограничено случаем стационарного осесимметричного течения. С помощью осреднения уравнений тонкого слоя с учетом вязкости, градиента гидростатического давления, центробежной и Кориолисовой сил получена система обыкновенных дифференциальных уравнений относительно толщины слоя, радиальной и окружной компоненты скорости. Проведен качественный анализ решений этой системы уравнений, получена классификация режимов течения. Получено, что при увеличении скорости вращения гидравлический прыжок смещается к периферии диска, при этом изменение толщины слоя на прыжке монотонно уменьшается до нуля. При определенной скорости вращения прыжок исчезает и решение, описывающее течение, становится непрерывным. Выявлено четыре качественно различных режима течения, которые различаются наличием и расположением зон докритического течения, где радиальная скорость течения меньше скорости распространения малых возмущений по поверхности жидкости.
Показано, что гидравлический прыжок расположен ближе к оси вращения, чем точка потери устойчивости течения по отношению к малым осесимметричным возмущениям [1].
В НИИ Механики МГУ имени М.В. Ломоносова построена экспериментальная установка для изучения подобных течений. Получено качественное соответствие между результатами расчетов и экспериментальными данными. Вместе с тем, наряду со стационарными осесимметричными режимами течения обнаружены волновые режимы (стационарные спиральные, осесимметричные капиллярные).
Работа выполнена по госбюджетному плану МГУ при частичной поддержке РФФИ (гранты 18-01-00762, 18-51-00006).
1.Могилевский Е. И., Шкадов В. Я. Течения тонких пленок вязкой жидкости по криволинейным вращающимся поверхностям // Изв. РАН. МЖГ. 2009. — № 2. — С. 18–32
Евгений Ильич Могилевский
Институт теоретической и прикладной механики им. С.А. Христиановича СО РАН
Введённый нами около 15 лет назад термин «детерминированная турбулентность» (ДеТу) относится к постпереходному погранслойному течению, которое выглядит как турбулентное (в соответствии с общепринятой точкой зрения, хотя она и нечётко определена), но обладает сильной степенью детерминированности. Такой тип турбулентности может возникать в пограничных слоях, в которых переход вызван конвективными типами неустойчивости. Первая экспериментальная реализация ДеТу была осуществлена около двенадцати лет назад [1, 2]. Последующие эксперименты (выполненные в Новосибирске и Лондоне) подтвердили возможность реализации ДеТу и показали огромные методические возможности этого подходя для изучения, как свойств турбулентных потоков, так и результатов различных вешних воздействий на мгновенную структуру турбулентности. Однако ряд важных аспектов проблемы исследования ДеТу оставался долгое время не изученным.
В частности, не было однозначного ответа на основной вопрос. «Точно ли соответствует ДеТу обычной случайной турбулентности?» При положительном ответе на этот вопрос, статистические свойства ДеТу (такие, как профили средней скорости, профили амплитуд пульсаций, спектры пульсаций, и др.) не должны зависеть от конкретной мгновенной реализации детерминированного турбулентного потока. Этот аспект проблемы был недавно подробно исследован [3] и обсуждается в настоящем докладе. Другой важный вопрос – о степени детерминированности, т.е. многократной воспроизводимости, мгновенной структуры ДеТу оставался также открытым. Недавние исследования привели, в частности, к обнаружению удивительного свойства пристенной турбулентности – универсального экспоненциального нарастания некогерентных компонент течения [3, 4].
Обсуждению этих и других свойств ДеТу, а также демонстрации огромных возможностей метода ДеТу при исследовании пристенной турбулентности и посвящён данный обзорный доклад. В докладе представлены результаты анализа свойств вихревых структур, возникающих в экспериментах в двумерном, первоначально ламинарном, пограничном слое с умеренным неблагоприятным продольным градиентом статического давления. В одной серии измерений вихревые структуры, типичные для турбулентного пограничного слоя воспроизводились многократно путём точного воспроизведения начальных контролируемых возмущений – волн Толлмина-Шлихтинга (ТШ) широкого частотно-волнового спектра. Возникновение и эволюция этих структур, и постепенное нарастание степени невоспроизводимости их свойств, тщательно исследовано. В другой серии измерений подробно изучена степень воспроизводимости статистических характеристик ДеТу при изменении мгновенной структуры турбулентности, создаваемой путём варьирования начального частотно-волнового спектра волн ТШ, генерируемых в пограничном слое. В докладе также показано, как метод ДеТу позволяет изучать воздействие внешних факторов на мгновенную структуру пристенной турбулентности. Этот подход позволил прояснить механизм снижения вязкого терния на стенке при помощи устройств разрушения крупных вихрей (LEBU), изучавшихся в ряде предшествующих экспериментов. Несмотря на широкую известность этих устройств, механизм их воздействия на поток был окончательно выяснен только после применения метода ДеТу [5].
Работа поддержана Программой фундаментальных научных исследований Российских академий наук в 2013-2020 гг. (проект № AAAA-A17-117030610128-8).
1.Borodulin V.I., Kachanov Y.S. and Roschektayev A.P. The deterministic wall turbulence is possible // Advances in Turbulence XI. Proceedings of 11th EUROMECH European Turbulence Conference, June 25–28, 2007, Porto, Portugal / J.M.L.M. Palma and A. Silva Lopes, eds. – Heidelberg: Springer, 2007, pp. 176–178.
2. Borodulin V.I., Kachanov Y.S. and Roschektayev A.P. Experimental detection of deterministic turbulence // Journal of Turbulence. 2011. – Vol. 12, No 23. P. 1–34.
3.Borodulin V.I., Kachanov Y.S. On the reproducibility of instantaneous and statistical characteristics of the deterministic turbulence // Theoretical and Applied Mechanics Letters // 2014. – Vol. 4, 062004.
4. Borodulin V.I., Kachanov Y.S. Experimental Study of Reproducibility of Instantaneous Structure of the Deterministic Wall Turbulence // Proceedings of 8th Intl. Symposium on Turbulence and Shear Flow Phenomena - TSFP-8. E.N.S.M.A. Poitiers, France, 2013,pp. 1-6.
5. V.I. Borodulin, Y.S. Kachanov, A.P. Roschektayev Application of the deterministic turbulence method to study of LEBU-device mechanism // Advances in Turbulence XII. Springer Proc. Phys. 132, Proc. 12th Eur. Turbulence Conf., September 7–10, 2009, Marburg, Germany / B. Eckhardt, ed. - Berlin: Springer, 2009, pp. 313–316.
Юрий Семенович Качанов
НИИ механики МГУ имени М.В. Ломоносова
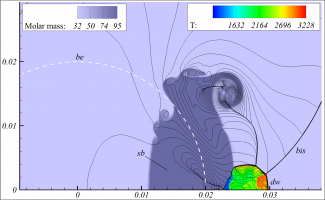
На основе уравнений Эйлера для совершенного газа с неоднородной молярной массой моделируется взаимодействие ударной волны в горючем газе с эллипсоидальным пузырем инертного газа повышенной плотности в двумерной постановке. Рассмотрены различные числа Маха M падающей волны и отношения длин полуосей пузыря. Для численного моделирования применяется конечно-объемный метод типа С.К. Годунова второго порядка аппроксимации, включающий HLLC-решатель локальных задач о распаде разрыва. Реакция горения газовой смеси моделируется с помощью двухстадийной кинетики Коробейникова-Левина.
Описаны различные режимы воспламенения смеси и показана их существенная зависимость как от интенсивности падающей волны, так и от формы пузыря. При достаточно больших числах Маха падающей волны инициирование горения смеси происходит непосредственно за счет разогрева в ударной волне. Для более слабых скачков воспламенение может происходить при отражении падающей ударной волны от границы раздела газов (рис. 1, слева), а для еще более слабых – в области фокусировки поперечных скачков вблизи подветренного полюса пузыря (рис. 1, справа).
Показано, что форма пузыря играет также важную роль, во многих случаях обеспечивая инициирование горения пузыря более слабой волной, или наоборот, отсутствие воспламенения по сравнению со сферическими пузырями.
Работа выполнена в НИИ механики МГУ имени М.В. Ломоносова с использованием ресурсов суперкомпьютерного комплекса МГУ имени М.В. Ломоносова при частичной финансовой поддержке Совета по грантам президента РФ (МК-3012.2019.1) и Российского фонда фундаментальных исследований (18-01-00793).
Олег Георгиевич Сутырин
Пермский государственный национальный исследовательский университет
Динамика возникающих в жидкости кавитационных пузырьков зависит от различных факторов, могут наблюдаться как коллапс пузырьков, так и их коалесценция и длительное существование относительно крупных пузырьков, как в объеме жидкости, так и вблизи твердых поверхностей [1].
Дегазация жидкости — процесс уменьшения содержания газа в жидкости. На данный момент существуют химические и физические способы дегазации. В основе химических методов удаления из воды, растворенных газов лежит их химическое связывание, достигаемое введением реагентов или фильтрованием через специальные загрузки. Сущность физических методов дегазации заключается в следующем: вода, содержащая удаляемый газ, приводится в соприкосновение с воздухом, если парциальное давление этого газа в воздухе близко к нулю; создаются условия, при которых растворимость газа в воде становится ничтожно малой.
В данной работе рассматривается ультразвуковой способ дегазации жидкости. При ультразвуковой обработке жидкости создается большое количество малых пузырьков, в которые мигрирует растворенный газ и увеличивает размер этих пузырьков. Далее, за счет силы Архимеда пузырьки поднимаются на поверхность воды и высвобождают находящийся внутри газ во внешнюю среду.
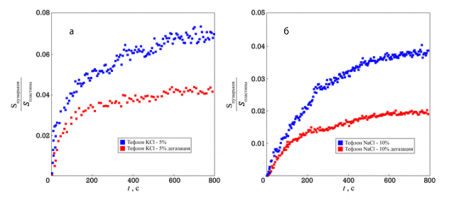
В настоящей работе проведены эксперименты по изучению динамики парогазовых пузырьков дрейфующих вблизи твердых поверхностей под действием ультразвука с использованием дистиллированной воды, а также растворами NaCl и KCl с различными концентрациями, для пластин из аморфного кварца, органического стекла и тефлона. Разработана методика оценки площади поверхности пластины покрытой пузырьками.
Эксперименты показали, что на скорость роста площади, занимаемой пузырьками, существенно влияет степень дегазации воды. При длительной дегазации воды пузырьковые кластеры на поверхности оргстекла практически не образуются. Однако, на поверхности тефлона можно выделить несколько зон в которых наблюдалось устойчивое прикрепление пузырьков, возможно, вследствие диффузии воздуха с открытой поверхности жидкости в кювете.
Экспериментально подтверждено различие в динамике роста площади, покрытой пузырьками, для тефлона и оргстекла. Результаты работы могут найти применение при объяснении влияния дегазации растворов на качество флотации руд, в частности сильвинитовой руды.
Исследование выполнено за счет гранта Российского научного фонда (проект № 19-31-90138).
1. K. A. Rybkin, Yu. K. Bratukhin, T. P. Lyubimova et al. Experimental study of formation and dynamics of cavitation bubbles and acoustic flows in NaCl, KCl water solutions // Journal of Physics: Conference Series / IOP Publishing. — Vol. 879. — 2017. — P. 012026.
Матвей Максимович Гончаров