Математическое моделирование контакта с проскальзыванием между колесом и дорогой
Автор: Галина Валерьевна Гусак
Организация: МГУ им. М.В. Ломоносова
Изучается контактное взаимодействие деформируемого колеса и недеформируемой дороги в ситуациях, когда колесо находится под действием различных видов статических нагрузок, а также при некоторых режимах движения.
«Щеточные» модели представляют периферию колеса в виде набора деформируемых элементов, стержней или пружинок [1, 2]. В отличие от моделей, основанных на методе конечных элементов, они допускают менее громоздкое математическое описание, позволяя при этом учитывать характер распределения сил в зоне контакта (ЗК), моделировать проскальзывание и ряд других эффектов, благодаря чему применяются для аналитического описания законов поведения деформируемого колеса.
В работе предложен новый механический аналог деформируемой периферии колеса, «стержневой протектор» [3], который принадлежит к классу щеточных моделей, однако опирается на иной набор гипотез нежели предшествующие модели данной группы [1, 2]. Колесо представлено твердым диском, окруженным по периметру набором радиально расположенных упругих стержней.
В зависимости от нагрузок, действующих на колесо, жесткостных и геометрических характеристик протектора, трения с дорогой, определяются границы зоны контакта, наличие или отсутствие проскальзывания, картина распределения реакций, величина, направление и точка приложения равнодействующей реакции, потери энергии за счет трения. Проводится анализ динамики колеса с учетом проскальзывания в контактной области. Рассматриваются следующие типы движения: качение без проскальзывания, качение с частичным проскальзыванием, движение «юзом».
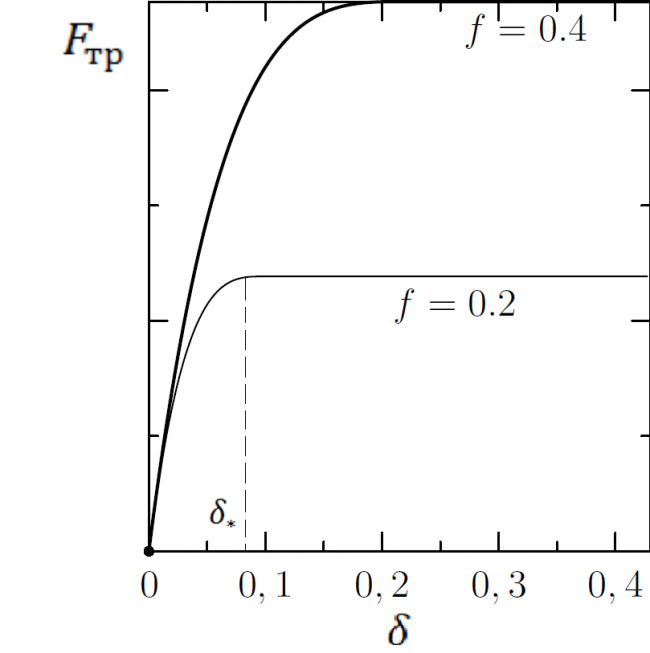
Получены выводы о зависимости силы трения от относительного проскальзывания в ЗК (рис.): сила трения минимальна при качении без проскальзывания; она возрастает с ростом участка проскальзывания в ЗК пока не достигнет предельного значения, равного по величине силе трения скольжения. Переход к предельному значению силы трения происходит, когда начинается скольжение всей ЗК. Предельное значение силы трения пропорционально вертикальной нагрузке (весу колеса). Найденная зависимость согласуется с теорией качения Картера, которая имеет экспериментальные подтверждения.
