Математическое моделирование процесса стабилизации жесткого ротора, вращающегося в электромагнитных подшипниках
Автор: Алексей Валерьевич Мухин
Организация: ННГУ им. Н.И. Лобачевского
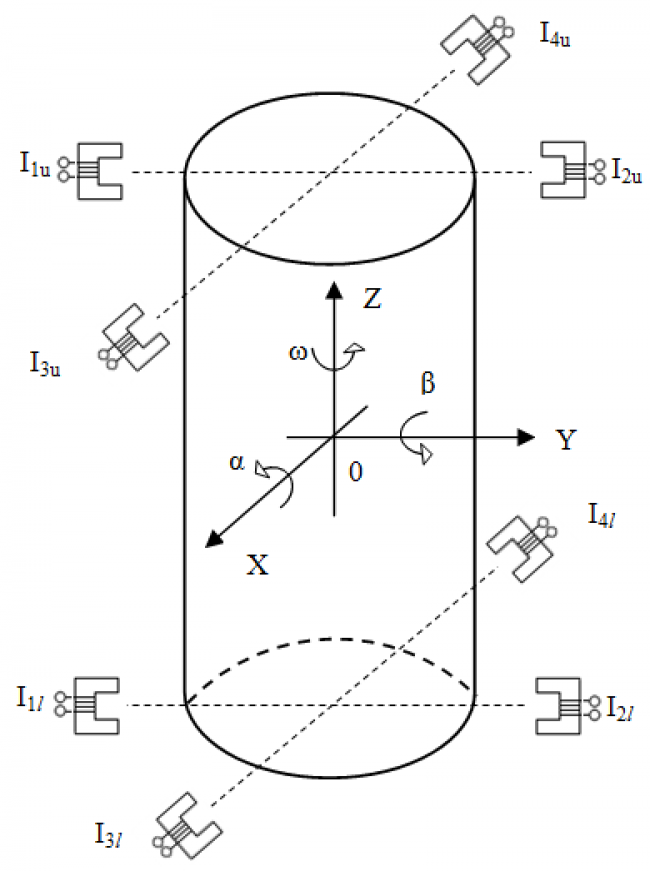
Рассмотрена задача оптимальной стабилизации механической системы, представляющей собой жесткий ротор, вертикально вращающийся в электромагнитных подшипниках (схема жесткого ротора, вращающегося в электромагнитных подшипниках – см. ниже) [1].
Фазовое пространство системы определялось двенадцатью переменными . Восемь первых переменных описывают механические параметры, а четыре последних – электрические параметры системы.
Для решения задачи формировался закон управления по выходу в форме линейного динамического регулятора полного порядка. В качестве измеряемых и управляемых параметров системы рассматривались токи в цепях электромагнитов. В качестве критерия оптимальности использовалась обобщенная -норма линеаризованной системы, позволяющая учесть как внешнее возмущение, так и начальное отклонение ротора.
В качестве математического инструментария использовались техника линеаризации исходной системы нелинейных дифференциальных уравнений [2], аппарат линейных матричных неравенств [3], а также методы теории выпуклой оптимизации [4].
Представлены результаты численных экспериментов математического моделирования динамики вращающегося ротора. Результаты показали, что измеряя только токи в цепях электромагнитов, можно синтезировать закон управления по выходу в форме линейного динамического регулятора полного порядка.
1.Мухин А.В. Математическое моделирование процесса стабилизации жесткого ротора, вращающегося в электромагнитных подшипниках // Труды НГТУ им. Р.А. Алексеева. 2020 (в печати).
2.Понтрягин Л.С. Обыкновенные дифференциальные уравнения. М.: Физматлит, 1974.
3.Баландин Д.В., Коган М.М. Синтез законов управления на основе линейных матричных неравенств. М.: Физматлит, 2007.
4.Gahinet P., Nemirovski A., Laub A. J., Chilali M. The LMI Control Toolbox. For Use with Matlab. User’s Guide.‑ Natick, MA: The MathWorks, Inc., 1995.
