НИИ механики МГУ, Москва
Графическая аннотация – рисунок, привязанный к каждому докладу на сайте конференции, - важный визуальный элемент, разъясняющий в научно-популярном стиле суть научной работы участника конференции. Из быстрого просмотра графической аннотации на сайте конференции каждый участник нашей конференции, не специализирующийся в данной области механики, должен получить общее представление о содержании доклада. Графическая аннотация должна по возможности ответить по крайней мере на один из следующих вопросов:
- В чем заключается суть предлагаемого метода исследования некоторой научной проблемы? В чем состоит актуальность и научная новизна?
- Какова область практического приложения результатов исследований? Какая выгода от использования результатов исследований?
Если не удается подготовить графическую аннотацию, отвечающую на эти вопросы, то в качестве графической аннотации можно использовать цветной рисунок, иллюстрирующий
- результаты расчётов, излагаемых в докладе;
- постановку эксперимента;
- схему исследуемого физического явления;
- другой иллюстративный материал, который будет излагаться в докладе.
Графическая аннотация должна быть рисунком в формате JPEG или PNG, размер которого не превышает 0.5 Мб.
С графическими аннотациями конференций 2017 и 2018 годов можно ознакомиться на сайте нашей конференции.
Оргкомитет
НИИ механики МГУ, Москва
Каждому участнику конференции предоставляется возможность сделать не более одного устного доклада и 1-2 стендовых доклада. На устном докладе участник представляет основное содержание своей работы. Ожидается, что изложение устного доклада даётся в научно-популярном стиле, понятном для широкой аудитории. На стендовых докладах, дополняющих устный доклад, участник делает сообщение о частных узкоспециализированных проблемах и результатах. Продолжительность устных докладов будет определяться исходя из числа участников (но не более 20 минут). Участнику необходимо направить в адрес Оргкомитета отдельную аннотацию для каждого доклада (и устного, и стендовых).
Оргкомитет
ФГБОУ ВО "Пермский национальный исследовательский политехнический университет"
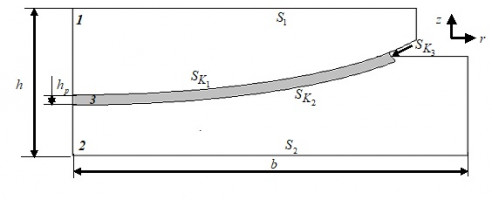
Ранее в [1] был отмечен ряд актуальных задач, связанных с геометрической конфигурацией опорных частей мостов. В работе рассмотрена задача анализа влияния толщины антифрикционного слоя на деформационное поведение конструкции сферической опорной части .
Характерные размеры сферической опорной части: максимальные высота 0,0483 м и ширина 0,155 м конструкции, толщина антифрикционной прослойки 3 0,004 м. В качестве материалов антифрикционной прослойки рассмотрено 6 материалов: три сверхвысокомолекулярных полиэтилена (СВМПЭ) разных производителей (мат. 1-3); два антифрикционных композиционных материала (мат. 4-5); модифицированный фторопласт (мат. 6).
В рамках серии численных экспериментов получены зависисмости распределения контактных параметров, интенсивности напряжения, интенсивности пластических деформаций и нормальных перемещений относительно свободного края слоя скольжения от толщины антифрикционной прослойки.
Установлено, что композиционные антифрикционные материалы больше подвержены деформированию. Данный эффект можно наблюдать на рис. 2: перемещения относительно свободного края прослойки из материалов 4-5 значительно больше и достигают 2,894 мм и 2,68 мм соответственно при толщине прослойки 4 мм, что в среднем в 5,6 раз больше, чем у других рассматриваемых материалов слоя скольжения.
Исследование выполнено за счет гранта Российского научного фонда (проект № 18-79-00147).
1. Adamov A.A., Kamenskikh A.A. The deformation behavior of modern antifriction polymer materials in the elements of transport and logistics systems with frictional contact // Advances in Intelligent Systems and Computing book series: Digital Science. – 2020. – Vol. 1114. – pp. 522-532.
Анна Александровна Каменских
Математический институт им. В.А. Стеклова Российской академии наук, Москва
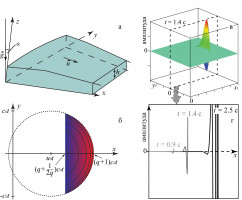
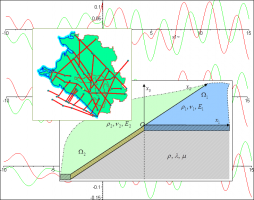
Течения потоков жидкости по наклонным поверхностям часто встречаются в природе и различных технических приложениях. С первой четверти XX века устойчивость таких потоков и развитие возмущений в них активно изучались аналитически, экспериментально, а позже и численно (см., например, [1, 2]). В настоящей работе аналитически в линейном приближении с помощью метода перевала изучается асимптотическое поведение локализованного по пространству и времени возмущения слоя линейно-вязкой жидкости на наклонной плоскости. Течение описывается уравнениями в гидравлическом приближении, то есть осреднёнными по глубине уравнениями МСС с учётом некоторых предположений (см., например, [3]). Рассматривается однородный неустойчивый поток на склоне постоянного уклона α (рис. 1а). Ранее эволюция трёхмерного локализованного возмущения открытого потока на вертикальной стенке исследовалась методом перевала в работах [2, 4]. В [2] (Глава 11, с. 327) рассматривалось течение, описываемое обобщённым уравнением Курамото-Сивашинского; в [4] — течение, описываемое системой уравнений Капицы-Шкадова.
Локализованное возмущение представляется суммой двойных интегралов Фурье, где интегрирование ведётся по всем вещественным волновым числам kx, ky (kx, ky — компоненты волнового вектора), суммирование — по корням дисперсионного уравнения (см. [5]). В начальный момент времени возмущение задаётся дельта-функцией. С помощью метода перевала определены размеры и форма области пространства, занятой растущим возмущением (рис. 1б), и поведение волны внутри этой области. (Обозначения: g — ускорение свободного падения, h — глубина потока, q = u0/c0, c0 = (gh0cosα)1/2, u0 — скорость невозмущённого потока, направленная вдоль оси x, нижний индекс «0» отмечает величины, относящиеся к невозмущённому течению.) Возмущение растёт внутри сегмента круга радиуса c0t с центром в точке x = u0t, y = 0. Гребни растущих волн — дуги окружностей с центром в той же точке (показаны серым на рис. 1б). Длина волны стремится к нулю при приближении к точке x = (q+1)c0t. Фазовая скорость возмущения превосходит групповую. Визуализация возмущения в пространстве приведена на рис. 1в.
Исследование выполнено за счет гранта Российского научного фонда (проект № 19-71-30012).
1. Алексеенко С.В., Накоряков В.Е., Покусаев Б.Г. Волновое течение пленок жидкости. — Новосибирск: ВО «Наука». Сибирская издательская фирма, 1992. — 256 с.
2. Chang H.-C., Demekhin E.A. Complex Wave Dynamics on Thin Films. D. Möbius and R. Miller. Elsevier. Amsterdam. 2002.
3. Эглит М.Э. Неустановившиеся движения в руслах и на склонах. — М.: Изд-во Моск. ун-та, 1986. — 96 с.
4. Demekhin E.A., Kalaidin E.N., Kalliadasis S., Vlaskin S.Yu. Three-dimensional localized coherent structures of surface turbulence. II. Λ solitons // Phys. Fluids. 2007. V. 19. 114104.
5. Zayko J., Eglit M. Stability of Downslope Flows to Two-Dimensional Perturbations. // Phys. Fluids. 2019. V. 31. 086601.
Юлия Сергеевна Зайко
Московский Государственный Университет им. М.В. Ломоносова
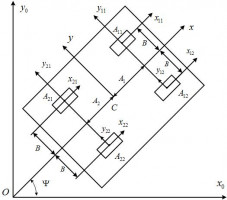
Рассматривается динамика корпуса двухосного четырехколесного аппарата (автомобиля, робота и т.д.) при попадании колес ведущей оси на «микст» – участок опорной плоскости с различными коэффициентами трения для колес одной оси. Для автомобиля такая ситуация возможна при въезде на обледенелую обочину, в лужу масла и т.п. Ранее в [1,2] было показано, что после завершения быстрого переходного процесса выравнивания контактных сил корпус аппарата получает импульс угловой скорости, способный привести к заносу. В зависимости от условий движения аппарата рассматриваются разные модели сил взаимодействия его колес с опорной плоскостью. Для описания динамики колес аппарата без потери сцепления с опорной плоскостью используются модель непроскальзывания и модель увода в продольном и поперечном направлениях, для описания скольжения колес – модель трения кулона и модель поликомпонентного сухого трения. Математические модели динамики аппарата формируются с использованием методов разделения быстрых и медленных движений, основанных на подходах фракционного анализа и теории сингулярных возмущений [3]. Возможность их применения связана с сильным разнесением постоянных времени движения аппарата на начальной стадии заноса [1–4]. Получены оценки импульсов угловой скорости, и показано, что моменты верчения колес слабо влияют на эти оценки, но важны при исследовании динамики корпуса аппарата на «миксте» после воздействия импульса угловой скорости. Описано развитие заноса, определяемого более медленной динамикой корпуса аппарата, для перечисленных случаев движения с уводом и со скольжением колес.
Благодарности. Данная работа была поддержана Фондом развития теоретической физики и математики «БАЗИС», грант 19-8-2-29-1.
1.Новожилов И.В., Павлов И.С., Фрольцов В.А. О поведении автомобиля на «миксте» // Механика твердого тела. 2001. № 3. C. 61–67.
2.Влахова А.В., Новодерова А.П. Занос колесного аппарата на «миксте» // Вестник Московского университета. Серия 1: Математика. Механика, издательство Изд-во Моск. ун-та (М.). №5.
3.Влахова А.В. Математические модели движения колесных аппаратов. М.-Ижевск: АНО «Ижевский институт компьютерных исследований», 2014. 148 с.
4.Влахова А.В., Новодерова А.П. Моделирование заноса аппарата с повернутыми передними колесами // Изв. РАН. МТТ. 2019. № 1. с.23-49.
Анна Павловна Новодерова
МГУ имени М.В. Ломоносова
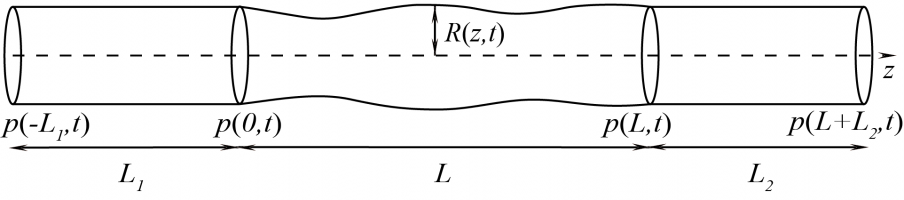
В биологических приложениях при течении жидкостей в моделях кровеносных сосудов возникают различные явления, которые оказывают влияние на характер течения и на деформацию стенок, что влечёт за собой дисфункциональные изменения в организме человека или животного.
Ранее в литературе исследовались, в основном, течения ньютоновской (линейно-вязкой) или идеальной жидкости [1, 2]. Хотя, кровь в средних и мелких сосудах обладает неньютоновскими свойствами. При этом одномерное моделирование течения крови по кровеносным сосудам является удобным инструментом для изучения динамики биологической жидкости в системе кровообращения.
Данное исследование проводилось классическими методами теории устойчивости, на основе ранее разработанной одномерной модели [3, 4]. Для трубок бесконечной длины рассматривались решения в виде бегущих волн и выводилось дисперсионное уравнение. Анализом его корней находились области неустойчивости в пространстве параметров.
Поскольку критерий устойчивости для сколь угодно большой длины трубки не совпадает с критерием устойчивости для бесконечно длинной трубки, то для определения границ устойчивости задача была исследована на нахождение области глобальной неустойчивости. В данном случае использовался асимптотический метод глобальной неустойчивости, разработанный А.Г. Куликовским [5].
Кроме того, для трубок конечной длины была решена задача на собственные значения. Граница устойчивости исследовалась численно с учетом упругости стенки трубы, продольного натяжения и длины трубки.
1.Grotberg J.B., Jensen O.E. Biofluid mechanics in flexible tubes // Ann. Rev. Fluid Mech. 2004. Vol.36. P.121–147.
2. Heil M., Hazel A.L. Fluid-Structure Interaction in Internal Physiological Flows // Ann. Rev. Fluid Mech. 2011. Vol.43. P.141–162.
3. Порошина А.Б., Веденеев В.В. Существование и единственность стационарного состояния упругой трубки при протекании через нее степенной жидкости // Российский журнал биомеханики. 2018. Т. 22. № 2. С. 196–222.
4. Веденеев В.В., Порошина А.Б. Устойчивость упругой трубки, содержащей текущую неньютоновскую жидкость и имеющей локально ослабленный участок // Труды МИАН. 2018.
Т. 300. С. 42–64.
5. Куликовский А.Г. Об устойчивости однородных состояний // Известия АН СССР. ПММ. 1966. Т. 30. Вып. 1. С. 148-153.
Анастасия Борисовна Подопросветова
Федеральный исследовательский центр Южный научный центр Российской академии наук (ЮНЦ РАН)
Механизмы сейсмических процессов до настоящего времени не получили исчерпывающего объяснения. Однако известно, что взаимодействие литосферных структур может привести к резонансным явлениям, способным спровоцировать землетрясения. Развитие механико-математических методов изучения взаимодействия блоковых отдельностей литосферы и диагностики характера дефекта в области их контакта, результаты применения которых в сочетании с интерпретацией результатов экспериментальных геофизических исследований [1] могут быть использованы для разработки и обоснования практических методик исследования процессов, определяющих характер сейсмичности территории, является весьма актуальным.
С помощью метода блочного элемента [2] исследуются задачи, описывающие процессы деформирования при статическом [3] и вибрационном воздействии некоторых классов разноразмерных блочных структур, используемых при моделировании областей взаимодействия плит и микроплит. На примере структуры, включающей покрытие из двух разнотипных контактирующих полуплоскости на трехмерной деформируемой подложке, исследован случай наличия вертикального разлома, способного вызвать локализацию напряженно-деформированного состояния в этой зоне. В качестве покрытий рассматриваются пластины Кирхгофа, движение которых описывается дифференциальными уравнениями в перемещениях [4]. В отличие от сложного алгоритма топологического метода блочного элемента при моделировании взаимодействие структур литосферы по прямолинейному участку границы может быть использован подход, позволяющий обеспечить более быстрое проведение расчетов.
Принятая модель для литосферных структур корового уровня в виде двумерных фрагментов покрытия на трехмерной подложке позволяет изучать особенности распространения сигнала в блочной среде, а также исследовать вопрос потери устойчивости покрытия. Имеющиеся данные о техногенной сейсмичности свидетельствуют о нарастании реакции верхних слоев литосферы на антропогенные воздействия, что делает их практически важным объектом изучения.
1.Мухин А.С., Павлова А.В., Телятников И.С. К методам исследования блочных литосферных структур // Экологический вестник научных центров Черноморского экономического сотрудничества. 2017. № 1. С. 65–73.
2. Бабешко В.А., Бабешко О.М., Евдокимова О.В. К теории блочного элемента // Доклады АН. 2009. Т. 427. №2. С. 183–187.
3. Telyatnikov I.S. Modeling of Deformation Processes in Lithospheric Structures during their Static Interaction // Thermal Science. 2019. Т. 23. № S2. pp. S591–S597.
4. Вольмир А.С. Гибкие пластинки и оболочки. М.: Государственное издательство технико-теоретической литературы, 1956. 422 с.
Илья Сергеевич Телятников
ИПМ им. М.В. Келдыша РАН.
В последнее время возрастает необходимость в улучшении условий работы сотрудников предприятий для повышения эффективности и снижения травмоопасности рабочих процессов. Использование промышленных экзоскелетов стало одной из основных концепций, направленных на решение данной задачи. Наибольшее распространение получили пассивные экзоскелеты, однако они не всегда могут необходимым образом и в нужный момент перераспределить нагрузку. Больший интерес вызывают полуактивные конструкции. Для определения моментов времени включения и выключения экзоскелетов требуется определять как основные действия оператора (ОД – ходьба, поднятие рук, и т.п.), так и переходные действия (ПД – процесс подъёма тяжести).
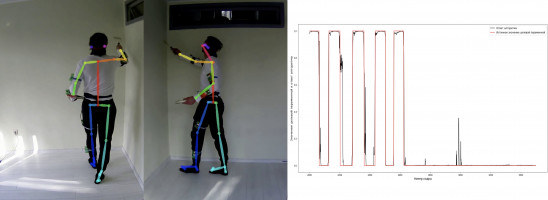
Целью работы является создание модели классификации действий человека с наилучшей метрикой качества, используя видеопоследовательности. В работе рассматривается задача классификации целевых действий человека по данным, получаемым с оптических датчиков (ранее было рассмотрено решение, основанное на инерциальных датчиках [2]). В качестве примера рассматривается задача покраски стены с двумя целевыми бинарными переменными: угол между плечом и туловищем больше или меньше критического, и целевое состояния – красит человек стену или нет.
В рамках задачи были сняты 5 пар параллельных видео с двух разных ракурсов длительностью по 6 минут каждое, на которых человек занимается покраской стены. Для получения информации с кадра была выбрана система OpenPose [1], которая для каждого кадра видео возвращала координаты ключевых точек человека, изображенного на кадре. Таким образом, была собрана обучающая выборка с номером кадра, двумя бинарными целевыми переменными и координатами 25 ключевых точек на человеке.
По результатам анализа построенных моделей был выбран алгоритм XGBClassifier. Для сравнения моделей были выбраны метрики ROC AUC и Accuracy. Полученные результаты обучения на первом целевом действии дают точность ROC AUC – 98% и Accuracy – 94%, на втором целевом действии – ROC AUC – 99% и Accuracy – 95%.
1. Cao Z. et al. OpenPose: realtime multi-person 2D pose estimation using Part Affinity Fields //arXiv preprint arXiv:1812.08008. – 2018.
2. Подопросветов А.В. и др. Разработка системы управления биомеханическим комплексом помощи работникам производственных предприятий // В сборнике: XII Всероссийский съезд по фундаментальным проблемам теоретической и прикладной механики сборник трудов в 4-х томах. 2019. С. 196-198.
Алексей Валерьевич Подопросветов
ЦАГИ, МГУ
На рисунке: Вверху – одна из первых исследуемых в работе компоновок разрабатываемого сверхлегкого самолета; в центре – зависимость подъемной силы от скорости взлета/посадки, внизу – зависимость подъемной силы от скорости полета.
Создание сверхлегких пилотируемых летательных аппаратов представляет практический интерес с точки зрения быстрой, безопасной и экономичной транспортировки грузов и человека.
Разрабатываемый сверхлегкий бесфюзеляжный самолет содержит несущую поверхность, стабилизатор, подвесную систему, систему управления и воздушный винт, отличается тем, что дополнительно содержит балку, крепящуюся к крылу и стабилизатору, четное количество расположенных на несущей поверхности электродвигателей с воздушными винтами, стропы, которые связывают несущую поверхность и балку с подвесной системой, на которой также расположен источник энергии, модуль дистанционного управления и электрическая трансмиссия, связывающая источник энергии с электродвигателями.
Уменьшение размеров летательных аппаратов ограничена размерами и весом летчика и превращает самолет по сути в некое подобие летательного костюма (рис. 1 вверху). Подготовлен обзор известных аналогов, показаны преимущества и области применения разрабатываемого летательного аппарата: например, экономичный и доступный личный транспорт, военные приложения, эвакуация, поисково-спасательные работы, перевозка грузов и оборудования широкого спектра назначения. Проектируемый самолет не требует аэродрома, обладает малым весом (40–45 кг), возможностью разборки для перевозки в личном и в общественном транспорте. Винтовая схема обеспечивает экономичность, дальность и продолжительность полета, при этом шум значительно ниже в отличие от реактивных аналогов. Оригинальная аэродинамическая компоновка обеспечивает низкие затраты электроэнергии двигателей при полном отсутствии вредных выбросов в атмосферу. Модификация аппарата для военных приложений обеспечивает высокую скорость, точность и низкую заметность. Статическая устойчивость в горизонтальном полете дает возможность пилоту освободить руки и использовать их для управления другими действиями. На рис. 1 внизу и в центре представлены результаты расчета зависимости подъемной силы летательного аппарата с крыльями различных конфигураций от скорости полета. Видно, что геометрия 10 обеспечивает достаточную подъемную силу при влете и посадке со скоростью 30–35 км/ч, которую можно снизить за счет применения разработанное ранее адаптивное крыло.
Иван Алексеевич Амелюшкин
Центральный аэрогидродинамический институт им. проф. Н.Е. Жуковского, Московский государственый университет имени М.В. Ломоносова

Использование гидрофобных покрытий представляет интерес в широкой области технических и бытовых приложений, в частности в задачах противодействия обледенению летательных аппаратов. Гидрофобные поверхности обладают своеобразными функциональными свойствами, к которым следует отнести водонепроницаемость, стойкость к коррозии, устойчивость к биообрастанию, к неорганическим, а в ряде случаев и к органическим загрязнениям. Благодаря многообразию управляемых свойств создание гидрофобных тел в настоящее время интенсивно развивается. Такие покрытия, как правило, эффективно работают при незначительных числах Вебера, рассчитанных по характерным размерам H рельефа поверхности We = HρV2/σ, (ρ – плотность жидкости, σ – коэффициент поверхностного натяжения, V – скорость удара капли). Однако при превышении поверхностной плотности кинетической энергии (переохлаждённой капли) некого критического значения, льдофобные свойства приводят к отрицательным эффектам ввиду проникновения жидкости в углубления и застывания в них. В случае динамического воздействия свойства гидрофобных/льдофобных покрытий определяются коэффициентами отскока капель в зависимости от числа Вебера. Достоверность полученных результатов обоснована сравнением с теоретическими и экспериментальными оценками других исследователей. Проведены параметрические исследования прилипания жидкости к рельефным покрытиям твердого тела, которые сформированы из комбинации гидрофобных и льдофобных материалов.
Иван Алексеевич Амелюшкин
ННГУ им. Н.И. Лобачевского
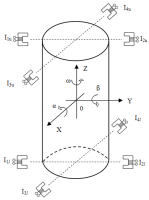
Рассмотрена задача оптимальной стабилизации механической системы, представляющей собой жесткий ротор, вертикально вращающийся в электромагнитных подшипниках (схема жесткого ротора, вращающегося в электромагнитных подшипниках – см. ниже) [1].
Фазовое пространство системы определялось двенадцатью переменными . Восемь первых переменных описывают механические параметры, а четыре последних – электрические параметры системы.
Для решения задачи формировался закон управления по выходу в форме линейного динамического регулятора полного порядка. В качестве измеряемых и управляемых параметров системы рассматривались токи в цепях электромагнитов. В качестве критерия оптимальности использовалась обобщенная -норма линеаризованной системы, позволяющая учесть как внешнее возмущение, так и начальное отклонение ротора.
В качестве математического инструментария использовались техника линеаризации исходной системы нелинейных дифференциальных уравнений [2], аппарат линейных матричных неравенств [3], а также методы теории выпуклой оптимизации [4].
Представлены результаты численных экспериментов математического моделирования динамики вращающегося ротора. Результаты показали, что измеряя только токи в цепях электромагнитов, можно синтезировать закон управления по выходу в форме линейного динамического регулятора полного порядка.
1.Мухин А.В. Математическое моделирование процесса стабилизации жесткого ротора, вращающегося в электромагнитных подшипниках // Труды НГТУ им. Р.А. Алексеева. 2020 (в печати).
2.Понтрягин Л.С. Обыкновенные дифференциальные уравнения. М.: Физматлит, 1974.
3.Баландин Д.В., Коган М.М. Синтез законов управления на основе линейных матричных неравенств. М.: Физматлит, 2007.
4.Gahinet P., Nemirovski A., Laub A. J., Chilali M. The LMI Control Toolbox. For Use with Matlab. User’s Guide.‑ Natick, MA: The MathWorks, Inc., 1995.
Алексей Валерьевич Мухин
Механико-математический факультет МГУ имени М.В. Ломоносова, Москва; НИИ механики МГУ имени М.В. Ломоносова, Москва
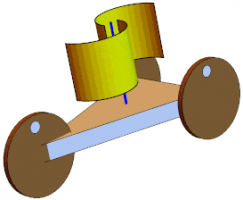
В работах [1-3] предложен феноменологический метод описания аэродинамических сил и моментов, действующих на ротор Савониуса в воздушном потоке. Данный метод позволяет описать аэродинамическое воздействие потока на ротор в виде функциональной зависимости сил и моментов от мгновенных значений обобщенных координат и скоростей, а также параметров систем, содержащих в своем составе ротор Савониуса. Как следствие такой подход дает возможность исследовать сложные механические системы, используя малопараметрические модели.
На основе упомянутого метода в данной работе исследуется динамика механической и электромеханической систем, в состав которых входит рассматриваемый тип ротора. А именно, построены математические модели ветроэнергетической установки на базе ротора Савониуса и ветродвижителя с ротором Савониуса. В первом случае энергия ветра преобразуется в электроэнергию, во втором – в полезную работу – движение ветромобиля, а ротор всегда выступает в качестве ветроприемного элемента. Описаны характеристики установившихся режимов движения и переходных процессов в зависимости от параметров и начальных условий.
Данное исследование в отличие от работы [4] учитывает зависимость аэродинамического воздействия на ротор и от угловой скорости вращения, и от угла поворота относительно набегающего потока. Обсуждается, какие свойства динамики изучаемых объектов можно уловить, используя не только усредненное значение момента на обороте, как это принято делать в таких случаях.
1. Мастерова А.А. Моделирование динамики малогабаритной ветроэнергетической установки на базе ротора Савониуса/ Труды конференции-конкурса молодых ученых. 13-17 октября 2017 г. / М.: Издательство Московского университета, 2018. – 140-147 с.
2. Мастерова А.А. Моделирование динамики колесной тележки, приводимой в движение с помощью ротора Савониуса/ Труды конференции-конкурса молодых ученых. 15-17 октября 2018 г. / М.: Издательство Московского университета – 98-105 с.
3. Мастерова А.А. Эмпирический подход к описанию воздействия потока на ротор Савониуса/ Тезисы конференции-конкурса молодых ученых Научно-исследовательского института механики МГУ имени М.В. Ломоносова 21-25 октября 2019 г. – с. 21.
4. Мастерова А.А. Динамика колесной тележки с ротором Савониуса / Всероссийская конференция молодых ученых-механиков YSM-2018. Тезисы докладов (4 − 14 сентября 2018 г., Сочи, «Буревестник» МГУ) / M.: Издательство Московского университета, 2018. – 116-116 с.
Анна Андреевна Мастерова
АО "ОКБМ Африкантов"
Для транспортировки и хранения радиоактивных материалов применяют специально разработанные для этого контейнеры, которые входят в состав транспортных упаковочных комплектов (ТУК).
В АО «ОКБМ Африкантов» разрабатывается ТУК, предназначенный для транспортировки и хранения отработанного ядерного топлива. В основу разработки ТУК легло выполнение требований нормативной документации (НП-061-05, НП-018-05, НП-001-15) и анализ напряженно-деформированного состояния конструкции при динамических воздействиях высокой интенсивности [1].
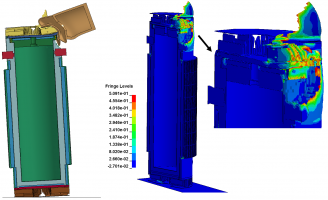
Оценка безопасности при падении самолета является важным проблемным вопросом при проектировании ТУК. Наиболее тяжелые последствия для конструкции могут быть вызваны прямым ударным воздействием двигателя (турбины) самолета. В данной работе рассматриваются вопросы моделирования высокоскоростного соударения турбины самолета с ТУК.
Корпус и несущие элементы ТУК смоделированы в полном соответствии с разработанной геометрией. При проектировании упрощенной конструкции, моделирующей турбину самолета, использовался график динамической нагрузки, полученный при ударном воздействии двигателя самолета Boeing 747 на жесткую стенку, из литературы [2].
В случае высокоскоростного динамического нагружения, сопровождающегося значительным пластическим деформированием, необходимо иметь истинные диаграммы деформирования, получаемые на основе расчетно-экспериментальных исследований путем определения параметров математической модели деформирования материалов. В данной работе использовались свойства конструкционных материалов, полученные из результатов экспериментальных исследований в условиях сжатия и растяжения при различных скоростях деформации и температурах.
Анализ соударения турбины самолета с ТУК был выполнен с использованием аттестованного программного комплекса ANSYS/LS-DYNA, основанного на методе конечных элементов и предназначенного для расчетного анализа высоконелинейных динамических процессов. Результаты проведенного анализа легли в основу формирования конечного облика разрабатываемой конструкции.
1. Виленский О.Ю., Душев С.А., Лапшин Д.А., Татарский А.М. Применение математического анализа при проектировании демпфирующих устройств для ТУК // Материалы XXI Международной конференции по вычислительной механике и современным прикладным программным средствам (ВМСППС’2019). 2019 г. С. 245-247.
2. K Shirai et al. Safety analysis of dual purpose metal cask subject to impulsive load due to aircraft engine crash // Journal of Power and Energy Systems, 3. 2009 г. P. 72-82.
Алексей Максимович Татарский
Институт физики прочности и материаловедения СО РАН
Технологические особенности получения аддитивных материалов приводят к образованию сложной микроструктуры, характеризующейся наличием границ раздела разного типа и геометрии, механической и кристаллографической текстур. Поскольку в рамках макромеханического подхода анализ деформационного поведения аддитивных материалов весьма затруднителен, разумным является использование многоуровневого моделирования с явным учетом микроструктуры материала [1]. В рамках подхода многоуровневого моделирования характеристики, полученные на нижележащих масштабах, использовались в качестве входных данных на более крупном масштабном уровне (рис. 1).
Согласно литературным данным зерна исследуемого сплава представляют собой дендриты, ветви которых отделены тонкой эвтектической прослойкой. Для определения свойств эвтектики (Al+Si) было проведено двумерное моделирование для фрагментов эвтектики, полученных путем графической обработки экспериментальных изображений (рис. 1а). Осредненные по объему характеристики были заданы в качестве кривой нагружения для эвтектической фазы на масштабе дендритной структуры зерна. На этом масштабе структура представляла собой ячейки дендритов, отделенные каркасной прослойкой эвтектической фазы (рис. 1б). Осредненные на этом масштабе характеристики деформационного отклика были использованы для описания упрочнения зерен трехмерной структуры на мезоуровне (рис. 1в).
Трехмерная модель поликристаллической структуры аддитивного алюминиевого сплава была сгенерирована методом пошагового заполнения. В соответствии с данными EBSD анализа модельный поликристалл содержал два характерных типа зерен – равноосные зерна по границам областей, имитирующих ванны расплава, и радиально направленные вытянутые зерна в их центральных частях (рис. 1в). Для описания деформационного отклика зерен были использованы определяющие соотношения физической теории пластичности для ГЦК кристаллов.
Для модельной трехмерной зеренной структуры в масштабе нескольких ванн расплава, была проведена серия расчетов растяжения вдоль, поперек направления сканирования и в направлении наращивания слоев. Проанализирована эволюция полей напряжений и пластических деформаций на мезоуровне. Показано, что на мезоуровне картины локализации пластической деформации и распределения напряжений коррелируют с областями равноосных и вытянутых зерен. Наибольшее отклонение локальных характеристик напряженно-деформированного состояния от среднего уровня наблюдалось для случаев растяжения вдоль направления сканирования и в направлении роста слоев.
1. Micromechanical Model of Deformation-Induced Surface Roughening in Polycrystalline Materials, Phys. Mesomech., 20, No. 3 (2017) 81.
Екатерина Дымнич
Федеральное государственное бюджетное образовательное учреждение высшего образования «Московский авиационный институт (национальный исследовательский университет)»
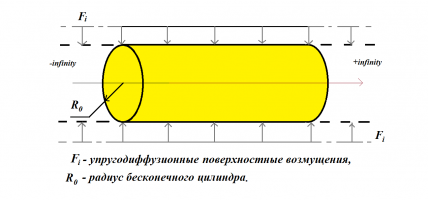
В представленной работе рассматривается одномерная полярно-симметричная связанная задача, целью которой является исследование НДС (напряженно-деформированного состояния) сплошного ортотропного многокомпонентного однородного бесконечного цилиндра, находящегося под действием равномерно распределенных нестационарных поверхностных возмущений упругодиффузионного характера. В работе учтено время релаксации диффузионных потоков в выбранном теле, что является существенным при моделировании быстропротекающих нестационарных процессов.
Математическая постановка задачи включает в себя дифференциальное уравнение движения сплошной среды и N неоднородных дифференциальных уравнений массопереноса. Замыкают математическую постановку задачи краевые условия, задаваемые на всей поверхности цилиндра. Начальные условия принимаются равными нулю.
Решение задачи в интегральной форме представляет собой свертки функций влияния данной задачи с функциями, задаваемыми в правых частях граничных условий. Для нахождения функций Грина используются разложение искомых в задаче функций в ряды Бесселя, а также интегральное преобразование Лапласа по времени. Оригиналы функций влияния определяются с помощью вычетов и таблиц операционного исчисления.
Николай Андреевич Зверев