О движении континуума плавящихся частиц

Автор: Олег Олегович Иванов

Соавторы: А.Н. Голубятников

Организация: Механико-математический факультет МГУ имени М.В. Ломоносова

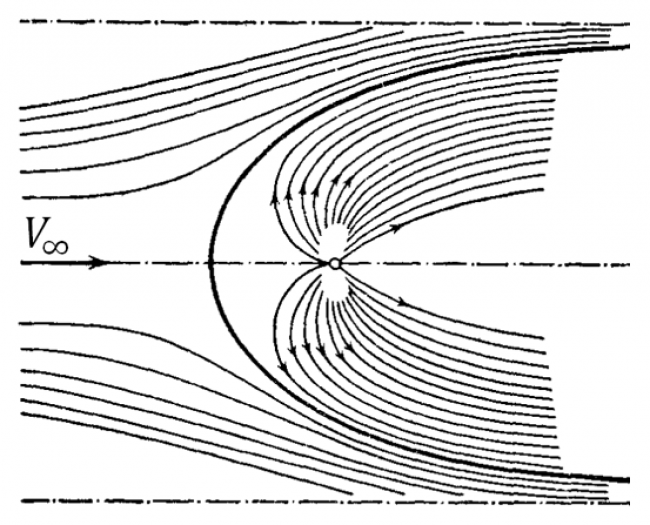
Известно, что при обтекании точечного источника (рис.1) с массовым расходом ρQ набегающим потоком со скоростью V, на источник будет действовать сила -ρQV. При движении сферической плавящейся частицы в собственном расплаве также необходимо   учитывать   изменение размеров частицы. Учет этих эффектов приводит к тому, что в уравнения движения частицы необходимо вводить реактивную силу, которая может существенно влиять на характер движения, как это было отмечено в [1] для случая идеальной жидкости. В работе [2] показано, что при наличии достаточно большого перепада температуры между частицей и расплавом данная сила может превышать силу вязкого сопротивления, что приводит к   ускорению. частицы. Получен простой критерий, определяющий характер движения частицы в зависимости от относительного перепада температуры, числа Прандтля и относительной разности плотностей расплава и частицы.

           На основании выведенных уравнений решается задача о случайном движении частицы, причём плавящейся за конечное время. Обнаружено, что среднеквадратичное отклонение такой частицы от начального положения за время плавления может быть даже неограниченно велико при больших перепадах температуры.

           Уравнения движения частицы в вязком расплаве при отсутствии внешних сил допускают интеграл движения, учитывающий изменение кинетической энергии, который может быть использован при построении общей статистической теории плавящихся частиц. Решается уравнение Лиувилля для системы невзаимодействующих частиц и выводится выражение для давления как функции плотности сохраняющегося числа частиц и общей равновесной температуры расплава. В результате получена гиперболическая система уравнений движения континуума частиц на фоне механических и тепловых параметров расплава.

           Для исследования особенностей движения континуума частиц решаются одномерные задачи с плоскими волнами: об однородном движении плавящихся частиц при нестационарном изменении температуры неподвижного расплава, а также о стационарном движении при постоянной температуре, проявляющая свойство запирания, связанное с невозможностью перехода через скорость звука, аналогичная газодинамической задаче о точечном источнике.

Работа частично поддержана грантом РФФИ № 17-01-00037.

1. А. Н. Голубятников. О взаимодействии плавящихся частиц о моделировании гравитации. // Вестник Нижегородского университета им. Н. И. Лобачевского, 2011. №4 (3). С. 728-729.

2. О. О. Иванов. К движению плавящейся частицы. // Вестник Московского университета. Сер. Математика. Механика, 2018 (в печати).