Обобщенная производная и ее использование для анализа микроструктуры гетерогенной среды
Автор: Алексей Владимирович Мишин
Организация: ИТПМ, НГУ
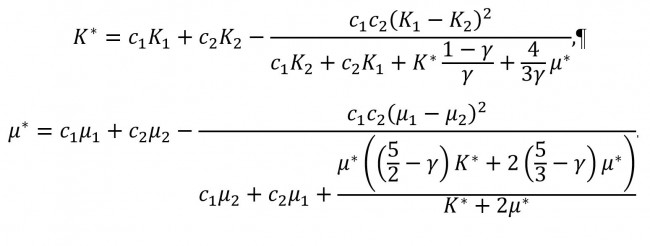
Одним из принципиальных нерешенных вопросов аналитического моделирования гетерогенных сред является учет микроструктуры системы (геометрии и физических свойств фаз). Введенной математической концепцией, направленной отобразить микроструктуру гетерогенной системы, выступает производная в обобщенном смысле [1]. Соответствующая производная содержит обычную и сингулярную составляющие. Сингулярная часть выражает разрывы поля на поверхности, что является естественным следствием анализа гетерогенной среды, характеризуемой развитой системой внутренних границ, разделяющих фазы с разными физическими свойствами. Проведение осреднения результата действия на поле производной в обобщенном смысле приводит к пространственной теореме осреднения в рамках теории смесей [2]. Описание гетерогенной среды осуществляется в рамках метода условных моментов [3]. Функционал данного подхода базируется на формализме функций Грина, условном осреднении и преобразовании Фурье. Методом условных моментов удается получить осредненные уравнения с эффективными коэффициентами упругости для среды в целом и для каждой фазы отдельно. Функция Грина, определяемая действующим оператором, отображает отклик поля в среде на приложенное воздействие. Исходя из этого ее роль в анализе характера распространения исследуемого поля по неоднородной системе является ключевой. В результате модификации операторов в исходной модели линейной теории упругости функция Грина характеризует микроструктурные особенности системы. Используя преобразованный в работе метод условных моментов, получены интегралы, содержащие осредненную функцию Грина и корреляционную функцию геометрии структуры. На основании этих членов микроструктура системы интегрально учтена во входящих в осредненные уравнения эффективных коэффициентах упругости.
1. Шварц Л. Математические методы для физических наук / Пер. с франц. М.: Мир, 1965.
2. Нигматуллин Р.И. – Основы механики гетерогенных сред // М. Наука., 1978.
3. Хорошун Л.П. О математической модели неоднородного деформирования композитов // Прикладная механика. 1996. №5 Том 32. С. 22-29.
2.
3.
