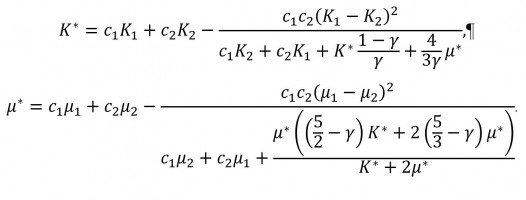НИИ механики МГУ имени М.В. Ломоносова
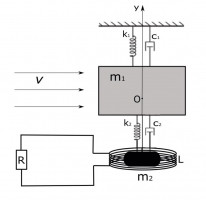
Рассматривается электромеханическая система, которая состоит из твердого тела (имеющего форму прямоугольного параллелепипеда), соединенного с помощью пружины с постоянным магнитом. Магнит и тело могут совершать возвратно-поступательное движение вдоль неподвижной горизонтальной прямой. Магнит находится внутри катушки индуктивности, а катушка включена в цепь, выходы которой замкнуты через нагрузочное сопротивление. Соответственно, при движении магнита в цепи возникает электрический ток. Система помещена в стационарный поток среды. Воздействие потока на магнит и катушку считается пренебрежимо малым.
Исследована устойчивость положения равновесия. Проведен параметрический анализ, получены достаточные условия устойчивости и неустойчивости. Путем численного моделирования были определены зависимости амплитуды и частоты колебаний тела, а также вырабатываемого тока и мощности от внешнего сопротивления и скорости потока. Показано, что в системе, поведение которой ближе к поведению системы с одной степенью свободы, амплитуда колебаний и вырабатываемая мощность меньше.
1. S. Tornincasa, M. Repetto, E. Bonisoli, F. Di Monaco. Energy harvester for vehicle tries: Nonlinear dynamics and experimental outcomes // Journal of Intelligent Material Systems and Structures, 2011, vol. 23, pp. 3-13.
2. T. Massai, J. Zhao, D. Lo Jacono, G. Bartoli, J. Sheridan The effect of angle of attack on flow-induced vibration of low-side-ratio rectangular cylinders // Journal of Fluids and Strustures, 2018, vol. 82, pp. 375-393.
Азим Эдгарович Курбанов
Федеральный исследовательский центр Институт прикладной физики РАН, Институт проблем машиностроения, Нижний Новгород
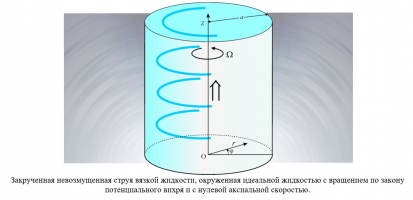
Исследуются свойства инерционных возмущений в закрученной струе вязкой жидкости как часть проблемы гидродинамической устойчивости. В невозмущенном состоянии в струе наблюдается линейное распределение азимутальной скорости и постоянная аксиальная скорость. Вне области центрального вихревого течения закрученной жидкости движение остального объема жидкости потенциальное. Жидкость во внешней области считается идеальной и имеет плотность, отличную от плотности вязкой жидкости струи (см. рис.). Жидкости предполагаются неэмульгирующими и несмешивающимися между собой. Сколь важна проблема устойчивости вихревых течений хорошо известно; менее известно, что еще Кельвин рассматривал инфинитезимальные возмущения цилиндрической поверхности колоннообразного вихря и показал, что этот вихрь без осевого течения и без учета вязкости нейтрально устойчив. Неустойчивость возникает, когда есть достаточно быстрое осевое течение в ядре, что было показано в работах Chandrasekhar S. и Krishnamoorthy V. Позднее Moore D.W. и Saffman P.G., Uberoi M.S. с соавт., Lessen M. с соавт., Loiscleux с соавторами выполнили более детальные исследования неустойчивости. Влияние вязкости жидкости во внутренней области вихря на устойчивость, за исключением очень частных случаев ранее не рассматривалось. Показано, что линеаризованная гидродинамическая задача допускает точные решения, поле скоростей в центральной области представляется в виде суперпозиции трех парциальных волн, во внешней области используется известное решение. Получено и исследовано дисперсионное уравнение в пределе коротких и длинных волн. Анализ дисперсионного уравнения в промежуточной области достаточно сложен, но, и это является одним из основных результатов работы, можно получить оценки параметров, при которых стационарное движение жидкости является устойчивым, без детального исследования дисперсионного уравнения.
1. Soldatov I.N., Klyueva N.V. Effects Of Viscosity On Inertial Waves In Swirling Jets //Heat and Mass Transfer and Hydrodynamics in Swirling Flows. AIP 2211, 030007 (2020); pp. 030007-1– 030007-6.
Злата Павловна Мишустова
НИИ механики МГУ
Движение по воде наземных транспортных средств вызывает большой интерес. Они не только являются амфибиями, то есть могут двигаться одновременно по воде и по суше, но и при движение по воде, значительно экономят топливо. В работе рассматривается машинка с гусеницей, которая оснащена грунт зацепами и при взаимодействии с водой создаёт тягу больше, чем колесо. Рассматривается плоскопараллельное движение и во всё время объект наклонён к горизонтальной поверхности под некоторым постоянным углом (в данной задаче рассматривались малые углы наклона). Таким образом, имеется две степени свободы – это координаты центра масс. Вертикальная указывает, насколько машинка погружена в воду, изменение горизонтальной координаты – линейную скорость. Эти два параметра будут основными, при изучении движения данного объекта.
На машинку действуют сила тяжести, подъёмная сила и сила сопротивления со стороны воды на её погруженную часть, а также тяга создаваемая гусеницей. В модели учитывается погружение машинки, это приводит к изменению сил, связанных с взаимодействием с водой. Тяга и подъёмная сила моделируются на основе данных экспериментов, которые проводились на водоканале НИИ механики МГУ. Дана оценка начальной скорости и угловой скорости вращения гусеницы, при которой машинка не будет тонуть. Приведены результаты моделирования и получен диапазон значений, при которых возможно движение по поверхности воды.
Андрей Петрович Голуб
Донской государственный технический университет , Ростов на Дону , Россия.
Индентирование — испытание материала методом вдавливания в поверхность образца специального инструмента — индентора, применяемое, для таких структур, как тонкие плёнки, микроструктуры, различные биологические ткани (зубные, костные и даже глазные).
Несмотря на их высокую прочность они часто ломаются или выходят из строя, как в результате естественного износа, так и из-за неаккуратных действий оператора
Производством данных узкоспециализированных инденторов занимаются всего несколько фирм и стоимость их продукции высока. Поэтому процесс получения новых инденторов затруднен, и это негативно влияет на динамику исследовательской работы.
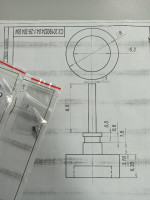
Авторами, был сконструирован специальный сферический индентор, состоящий из двух частей -сферы и держателя.
Сферы изготавливались отдельно из керамики и сапфира. Держатель был изготовлен для идеальной фиксации в индентометре NANOTEST 600 PLATFORM 3 (Micro Materials Ltd).
За основу корпуса держателя был взят вытачиваемый на металлообрабатывающем станке корпус из нержавеющей стали Х13. Были изготовлены корпуса для установки сферических наконечников различных диаметров: 200 мкм, 400 мкм, 500 мкм, 790 мкм, 1000 мкм, 5000 мкм, 6350 мкм.
Для установки сферы в держатель и максимально точного их позиционирования друг относительно друга, была разработана специальная методика. Сфера устанавливалась неподвижно в специальную форму из PLA, заливалась эпоксидной смолой и выдерживалась сутки для полной полимеризации. Получившуюся конструкцию устанавливали в шлифовальный станок MetaServ 250 (BUEHLER) и стачивали сферу на 1/20 диаметра. Далее, проводили совмещение усеченной сферы с держателем при помощи микрометрического винта. Связующим звеном между усеченной сферой и держателем был цианакрилат смешанный с ОСЧ ацетоном в объемной пропорции 1:1. Проверка качества соединения и позиционирования проводилась при помощи рентгеновского томографа Xradia 520 Versa (Carl Zeiss X-ray Microscopy, inc).
Иван Олегович Харчевников
Донской Государственный Технический Университет
Индентирование — испытание материала методом вдавливания в поверхность образца специального инструмента — индентора, применяемое, для таких структур, как тонкие плёнки, микроструктуры, различные биологические ткани (зубные, костные и даже глазные).
Несмотря на их высокую прочность они часто ломаются или выходят из строя, как в результате естественного износа, так и из-за неаккуратных действий оператора.
Производством данных узкоспециализированных инденторов занимаются всего несколько фирм и стоимость их продукции высока. Поэтому процесс получения новых инденторов затруднен, и это негативно влияет на динамику исследовательской работы.
Авторами, был сконструирован специальный сферический индентор, состоящий из двух частей -сферы и держателя.
Сферы изготавливались отдельно из керамики и сапфира. Держатель был изготовлен для идеальной фиксации в индентометре NANOTEST 600 PLATFORM 3 (Micro Materials Ltd).
За основу корпуса держателя был взят вытачиваемый на металлообрабатывающем станке корпус из нержавеющей стали Х13. Были изготовлены корпуса для установки сферических наконечников различных диаметров: 200 мкм, 400 мкм, 500 мкм, 790 мкм, 1000 мкм, 5000 мкм, 6350 мкм.
Для установки сферы в держатель и максимально точного их позиционирования друг относительно друга, была разработана специальная методика. Сфера устанавливалась неподвижно в специальную форму из PLA, заливалась эпоксидной смолой и выдерживалась сутки для полной полимеризации. Получившуюся конструкцию устанавливали в шлифовальный станок MetaServ 250 (BUEHLER) и стачивали сферу на 1/20 диаметра. Далее, проводили совмещение усеченной сферы с держателем при помощи микрометрического винта. Связующим звеном между усеченной сферой и держателем был цианакрилат смешанный с ОСЧ ацетоном в объемной пропорции 1:1. Проверка качества соединения и позиционирования проводилась при помощи рентгеновского томографа Xradia 520 Versa (Carl Zeiss X-ray Microscopy, inc).
Алексей Сергеевич Леднов
НИИ Механики МГУ
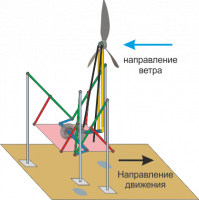
Рис.: Стопоходящая машина с ветроприводом
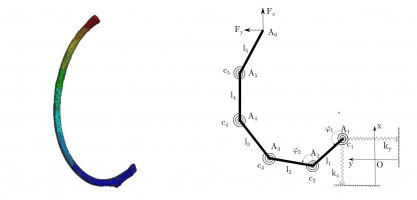
Рассматривается задача о движении стопоходящей машины Чебышева [1] с пропеллерной ветротурбиной по абсолютно шероховатой горизонтальной плоскости в стационарном потоке ветра, направленном вдоль линии движения корпуса. Ветроприёмная установка преобразует энергию ветра в энергию вращения и передаёт её рабочему валу стопоходящей машины (рис.1). Другие источники энергии отсутствуют. Целевым режимом является режим, при котором корпус машины перемещается против ветра с постоянной средней скоростью.
Детально описана кинематика стопоходящего механизма. В частности, показано, что вертикальные смещения центра масс на два порядка меньше характерного размера механизма. Описаны дополнительные допущения, которые позволяют рассматривать механизм как систему с одной степенью свободы.
При описании динамики системы использована квазистатическая модель аэродинамического воздействия [2].
Построена математическая модель, составлены уравнения движения в форме динамической системы второго порядка. Исследованы установившиеся режимы движения, найдены неподвижные точки и условия их устойчивости. Показано, что в некотором диапазоне параметров существует притягивающий установившийся режим движения, при котором корпус машины перемещается против ветра. Проанализировано влияние коэффициента лобового сопротивления корпуса.
1. Чебышев П. Л. Избранные труды. М.: Изд-во Академии Наук СССР, 1955. 929 с.
2. Локшин Б. Я., Привалов В. А., Самсонов В. А. Введение в задачу о движении тела в сопротивляющейся среде. М.: Изд-во МГУ, 1986. 86 с.
Михаил Андреевич Гарбуз
Томский государственный университет
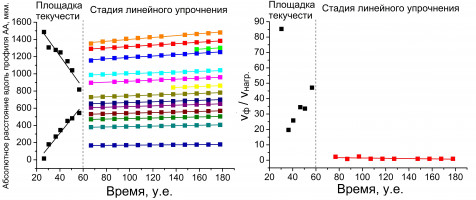
Проведён численный анализ стадий пластической деформации: площадки текучести и стадии линейного деформационного упрочнения низкоуглеродистой стали. При пластическом течении одни максимумы пластической деформации исчезают, а другие становятся ведущими. Последние обеспечивают основу для формирования раннего макроскопического очага разрушения. На основе полученных кинетических диаграмм выявлены особенности локализации пластической деформации на стадии линейного упрочнения. Применяется конечно-разностный анализ на основе микроструктуры. Был применён метод пошагового заполнения для получения представительного объёма поликристаллического образца.
Показано, что полосы Людерса распространяются неоднородно, со средним отношением скорости фронта к скорости нагружения равным ≈35, что хорошо согласуется с данными, полученными в экспериментах. Также показано, что абсолютное положение максимумов распределения пластической деформации изменяется со скоростью, равной скорости нагружения. Последнее свидетельствует о том, что взаимное расположение максимумов не меняется в процессе пластического течения.
Артём Олегович Чирков
Тюменский Научный Центр СО РАН
При проектировании и сооружении зданий, скважин, трубопроводов, а также других объектов, постоянно находящихся в условиях отрицательных температур, необходимо учитывать промерзание и протаивание грунтов. В тёплый период поверхностный слой грунта, подстилаемый многолетнемерзлыми породами, чаще всего высокопористый песок, оттаивает и образует переувлажненный слой породы. Для стабилизации грунта используют термостабилизаторы — охлаждающие устройства необходимые для повышения несущей способности грунта путём охлаждения и замораживания [1]. При охлаждении протаявшего слоя термостабилизатором, в пористой среде возникают градиенты температуры, приводящие к конвекции. В большинстве случаев, при моделировании конвективных течений не учитывается наличие максимума плотности воды (в окрестности 4° С), но при охлаждении грунта до 0°С, в высоко проницаемых грунтах этим явлением пренебрегать нельзя.
Цель данной работы - оценить влияние конвективного теплопереноса на процесс охлаждения термостабилизатором насыщенной водой пористой среды при учете явления инверсии плотности и продемонстрировать различия с расчетами, в которых не учитывается данное явление.
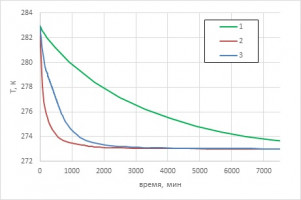
Для этого численно моделируется процесс охлаждения водонасыщенной пористой среды в теплоизолированном сосуде с вертикальным охлаждающим элементом. Проницаемость пористой среды характерна для высокопроницаемых среднезернистых песков и равняется 2,2*10-6 м2[2]. Расчеты выполнены для трёх различных случаев: в первом, расчёты без учёта конвекции; второй, без учета наличия максимума плотности воды и третий, расчёты с учетом максимума плотности воды. На рисунке 1 представлено изменение средних температур для этих случаев.
Конвективное течение значительно влияет на скорость остывания воды в поровом объёме (кривые 1 и 3). Причём, чем выше проницаемость водонасыщенной пористой среды, тем остывание за счёт конвекции происходит быстрее. В нашем случае расчётный объем остывает до температуры 273,5К за 1 сутки 4 часа, а без учета движения жидкости остывание происходит за 5 суток 14 часов (медленнее в 4,8 раза). При этом, если не учитывать максимум плотности воды (кривая 2), то средние скорости значительно выше, течение не замедляется, остывание в объёме происходит быстрее, за 18 часов.
Из проведенного исследования следует, что при решении теплотехнических задач в системах, содержащих высокопроницаемые влагонасыщенные грунты, необходимо учитывать конвективные течения, и предпочтительнее использовать модели воды, учитывающие её максимум плотности, так как ошибка при определении времен остывания может быть значительна (в наших расчётах в 1,5 раза).
Людмила Николаевна Филимонова
Институт автоматизации проектирования РАН, Москва
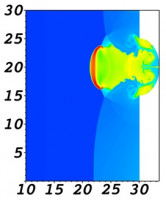
В данной работе проводится математическое моделирование воспламенения газовой смеси в канале с торцевой стенкой, состоящей из двух эллиптических участков, разнесенных плоской стенкой [1]. Математическая модель основана на решении системы уравнений Эйлера, дополненной моделью кинетики горения водородно-кислородной смеси. Рассматривается применение как глобальной одностадийной модели с параметрами [2], так и детальной модели горения [3],. В начальный момент времени на торцевую стенку подается УВ. Расчеты проводятся с использованием неструктурированных треугольных сеток.
Для обеих моделей распространение УВ по области с отражателем приводит к формированию таких структур, как тройные точки, ножки Маха, контактные разрывы с вихрями С1 и С2, отраженные волны (см. Рисунок). Отражение волны сопровождается образованием струи, направленной от торца. Струя формирует грибовидные структуры и неустойчивости Кельвина-Гельмгольца (K), которые воспламеняются при достижении газодинамическими параметрами повышенных значений. В работе обсуждаются результаты, полученные с использованием двух моделей химической кинетики.
Александр Игоревич Лопато
МГУ имени М.В.Ломоносова
Была поставлена глобальная задача моделирования грудной клетки для применения в лечении пациентов с килевидной деформацией. Подобное моделирование, особенно с помощью программ конечно-элементного анализа1, является своевременным и отвечающим запросам современной медицины.
В данном исследовании была построена механическая модель плоского ребра под нагрузкой, приложенной к его концу. Модель ребра состоит из 5 абсолютно твердых стержней, соединенных между собой спиральными пружинами и расположенных в одной плоскости. Спиральная пружина в начале первого стержня препятствует повороту этого стержня в плоскости. Также начало первого стержня соединено цилиндрическими пружинами с двумя перпендикулярными друг другу неподвижными плоскостями, что моделирует податливость в синовиальном суставе головки ребра. В изначальном положении все пружины не деформированы.
Для данной системы были получены уравнения равновесия под действием плоской силы, приложенной к свободному концу ребра. При известных жесткостях пружин и геометрических параметрах ребра данная система позволит быстро вычислять деформированное состояние ребра. Геометрические параметры, а именно длины стержней и углы между ними в недеформированном состоянии были найдены с помощью специализированной медицинской программы 3D Slicer, позволяющей сегментировать необходимые области по КТ сканам пациентов. Для нахождения решения уравнений равновесия необходимо идентифицировать параметры – жесткости пружин.
Жесткости пружин находились из гипотезы равенства перемещений свободного конца ребра в стержневой модели и в модели ребра как криволинейной линейно-упругой однородной изотропной плоской балки. Перемещения в балочной модели находились численно с помощью интеграла Мора.
Также было произведено моделирование ребра в программе конечно-элементного анализа Ansys. Ребро моделировалось линейно-упругим изотропным материалом. Механические характеристики материала, такие как модуль Юнга, были взяты из литературы1. Для конечно-элементной модели было найдено напряженно-деформированное состояние. Различие перемещений свободного конца в рассмотренных моделях составляет не более 10%.
Иван Викторович Алпатов
НИИ механики МГУ имени М.В. Ломоносова
Работа металлических конструкций при повышенных температурах в условиях растяжения иногда приводит к потери устойчивости. Изучение этого процесса при повышенных температурах представляет собой большой интерес, особенно поиск момент локализации деформаций. Известные на сегодняшний день критерии появления локализации деформаций в образце можно разделить на четыре группы: три детерминированных критерия - максимальной силы [1, 2], деформационные [3] и временные критерии [4, 5], а так же критерии, основанные на глубоком машинном обучении [6] и др.
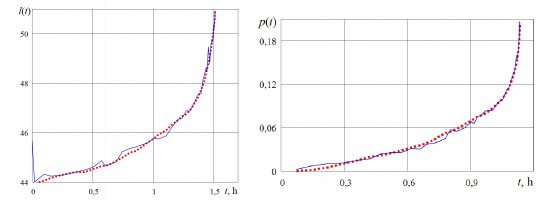
Экспериментальные испытания проводились при постоянной температуре 400°С с постоянной растягивающей нагрузкой в НИИ механики МГУ им. М.В. Ломоносова. Разработанный бесконтактный метод измерения [7] использован для измерения параметров образца. Полученные механические характеристики моделируются градиентным бустингом и нейронными сетями по фотографиям процесса деформирования. Промоделированы: длина образца, деформация образца и время локализации деформаций.
Моделирование методом градиентного бустинга показало, что алгоритм потерял обобщающую способность уже на уменьшенном наборе данных, поэтому в дальнейшем не рассматривался. Пример зависимости p(t) для экспериментов № 13 приведен на рисунке слева.
Нейросетевой анализ продольной деформации дал общую ошибку ~10 %. Для дальнейшего снижения ошибки была построена линейная регрессия на прогнозах трех нейронных сетей с наилучшими наборами гиперпараметров. Это позволило снизить ошибку моделирования до 3,6 % на всей выборке. Пример полученного результата для эксперимента №17 приведен на рисунке справа.
Времена локализации моделировались искусственной нейросетью для размерного и безразмерного значения. Использовались нейросеть с четырьмя выходами и четыре отдельных нейросети с одним выходом. Последняя показала лучший результат – 1.5 % на всей выборке данных.
1.Hora P, Tong L, Berisha B. Modified maximum force criterion, a model for the theoretical prediction of forming limit curves. Int. J. Mater. Form., 2013; 6: 267-279. https://doi.org/10.1007/s12289-011-1084-1.
2. Aretz H. An extension of Hill’s localized necking model. Int. J. Eng. Sci., 2010; 48:312-331.
3. Martínez AJ, Vallellano C, Morales D, Garc-Lomas FJ. On the Experimental Detection of Necking in Stretch‐Bending Tests. AIP Conference Proceedings 1181, 2009; 79: 500-508. https://doi.org/10.1063/1.3273668.
4. Wilshire В, Burt Н. Long-term creep design data for forged ICr—lMo—0,25V steel. Strength, Fracture and Complexity, 2006; 4: 65-73.
5. Srinivas B, Janaki P, Ganesh R. Application of a few necking criteria in predicting the forming limit of unwelded and tailor-welded blanks. Strain Analysis for Engineering Design, 2010; 45(2): 79-96.
6. Applications of Deep Learning for Computer Vision. Retrieved from https://machinelearningmastery.com/applications-of-deep-learning-for-computer-vision; 3 May 2019.
7. Teraud WV. An experimental research of high temperature strain localization and a method for non-touch measurements at a high temperature experiments. In: Proceedings of the First International Conference on Theoretical, Applied and Experimental Mechanics. Structural Integrity. Springer, Cham, 2018; 5: 124-130.
Валентин Викторович Терауд
Московский авиационный институт НИИ
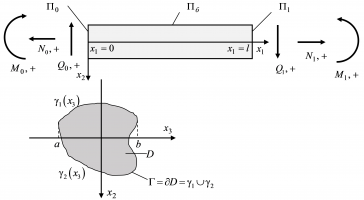
Для надежной работы ряда технических систем, в том числе летательных аппаратов, очень важным является учет взаимодействия множества различных параметров, характеризующих разнообразие видов внешних воздействий. При этом комплексное описание воздействия нагрузок различной физической природы на конструкцию и её отдельные элементы требует более глубокого понимая сути протекающих при этом процессов. В данной работе на примере нестационарного изгиба свободно опертой балки, как одного из основных элементов строительных конструкций, исследуется взаимосвязь механического, температурного и диффузионного полей.
Рассматриваемый вопрос очень важен при расчете корпусов авиадвигателей, фюзеляжей самолётов и ракет, для которых динамические изменения, связанные с внутренним переносом вещества при воздействии критических температур, и под действием механической нагрузки, могут привести к катастрофическим последствиям. Правильное понимание и применение законов диффузии, теории упругости и законов, описывающих температурное воздействие, позволяет избежать непредсказуемых и нежелательных изменений в авиаконструкциях, происходящих под влиянием нестационарных нагрузок различного характера.
Для постановки задачи используется модель связанной термоупругой диффузии для однородного ортотропного многокомпонентного континуума [1-4]. Модель нестационарного изгиба для упругодиффузионной балки Эйлера-Бернулли строится с помощью вариационного принципа Даламбера [3-5]. При этом предполагается, что:
1. Поперечные прогибы считаются малыми. Сечения, перпендикулярные к оси балки до деформации, остаются плоскими и после деформации (гипотеза плоских сечений);
2. Поперечные сечения после деформации остаются нормальными к изогнутой оси балки (гипотеза Бернулли- Эйлера);
3. Боковая поверхность балки свободна от нагрузок и тепломассоперенос на ней отсутствует, что позволяет считать балку несжимаемой в поперечном направлении.
Для решения полученной задачи, используется интегральное преобразование Лапласа по времени и разложение в ряды Фурье по пространственной координате. Обращение преобразования Лапласа осуществляется аналитически с помощью вычетов и таблиц операционного исчисления. Для расчетного примера, иллюстрирующего взаимодействие физических полей, рассматривается балка прямоугольного сечения, выполненная из трехкомпонентного материала, состоящего из алюминия (93,5%), меди (4,5%) и цинка (2%).
1.Aouadi M., Miranville A. Quasi-stability and global attractor in nonlinear thermoelastic diffusion plate with memory // Evolution equations and control theory. 2015. Vol. 4. No 3. P. 241-263
2.Bhattacharya D., Kanoria M. The influence of two temperature generalized thermoelastic diffusion inside a spherical shell // International Journal of Engineering and Technical Research (IJETR). - 2014. - Vol. 2, Is. 5. - P. 151-159
3. Tarlakovskii D.V., Zemskov A.V. An Elastodiffusive Orthotropic Euler-Bernoulli Beam with Considering Diffusion Flux Relaxation // Math. Comput. Appl. – 2019. – Vol. 24, Is. 1, 23; doi:10.3390/mca24010023
4. Zemskov A.V., Tarlakovskii D.V. Unsteady Vibration Model of the Euler-Bernoulli Beam Taking into Account Diffusion // IOP Conf. Series: Journal of Physics: Conference Series. – 2019. – Vol. 1158. – 042043 doi:10.1088/1742-6596/1158/4/042043
5.Le, K.C., Vibrations of shells and rods, Springer Verlag, Berlin, 1999
Георгий Михайлович Файкин
ИТПМ, НГУ
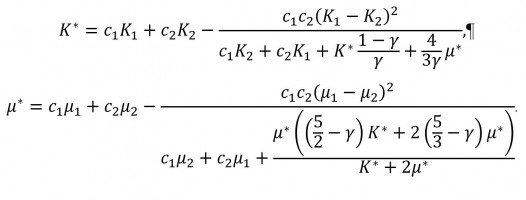
Одним из принципиальных нерешенных вопросов аналитического моделирования гетерогенных сред является учет микроструктуры системы (геометрии и физических свойств фаз). Введенной математической концепцией, направленной отобразить микроструктуру гетерогенной системы, выступает производная в обобщенном смысле [1]. Соответствующая производная содержит обычную и сингулярную составляющие. Сингулярная часть выражает разрывы поля на поверхности, что является естественным следствием анализа гетерогенной среды, характеризуемой развитой системой внутренних границ, разделяющих фазы с разными физическими свойствами. Проведение осреднения результата действия на поле производной в обобщенном смысле приводит к пространственной теореме осреднения в рамках теории смесей [2]. Описание гетерогенной среды осуществляется в рамках метода условных моментов [3]. Функционал данного подхода базируется на формализме функций Грина, условном осреднении и преобразовании Фурье. Методом условных моментов удается получить осредненные уравнения с эффективными коэффициентами упругости для среды в целом и для каждой фазы отдельно. Функция Грина, определяемая действующим оператором, отображает отклик поля в среде на приложенное воздействие. Исходя из этого ее роль в анализе характера распространения исследуемого поля по неоднородной системе является ключевой. В результате модификации операторов в исходной модели линейной теории упругости функция Грина характеризует микроструктурные особенности системы. Используя преобразованный в работе метод условных моментов, получены интегралы, содержащие осредненную функцию Грина и корреляционную функцию геометрии структуры. На основании этих членов микроструктура системы интегрально учтена во входящих в осредненные уравнения эффективных коэффициентах упругости.
1. Шварц Л. Математические методы для физических наук / Пер. с франц. М.: Мир, 1965.
2. Нигматуллин Р.И. – Основы механики гетерогенных сред // М. Наука., 1978.
3. Хорошун Л.П. О математической модели неоднородного деформирования композитов // Прикладная механика. 1996. №5 Том 32. С. 22-29.
2.
3.
Алексей Владимирович Мишин
Кафедра теоретической механики и мехатроники, механико-математический факультет МГУ
Введение: Исследование капсульных водных роботов - одна из актуальных проблем современной науки. Такие роботы могут применяться даже в медицинских целях. Подробный обзор исследований жидких капсульных роботов можно найти в [1]. Среди классических результатов в этой области можно отметить такие работы, как [2-3].
Описание системы: Исследуется подводный капсульный робот с одиночным внутренним маховиком. Робот совершает плоскопараллельное движение. Таким образом, система имеет четыре степени свободы и один управляющий вход. Математическая модель построена в виде динамической системы 5-го порядка. Для этого применяется квазистатическая модель взаимодействия с жидкостью. Эта модель позволяет не только проводить эффективный параметрический анализ, но и выявлять особенности движения, связанные с наличием боковой составляющей гидродинамической силы. Построена стратегия управления.
Результаты: Показано, что боковая сила обеспечивает возможность необратимого движения центра масс в желаемом направлении. Таким образом, перспективно создание подводных капсульных роботов и алгоритмов управления ими на основе использования боковой силы. Результаты моделирования подтверждены экспериментами с прототипом капсульного робота. Подтверждено качественное соответствие модели и экспериментов.
Ключевые слова: подводный робот, движение внутренней массы, квазистатическая модель,
[1] KILIN A, KLENOV A, TENENEV V: Controlling the movement of the body using internal masses in a viscous liquid. Computer research and modeling 2018, 10(4):445-460.
[2] KOZLOV V, RAMODANOV S: The Motion of a Variable Body in an Ideal Fluid. Prikl. Mat. Mekh. 2001, 65(4):592–601 (in Russian).
[3] CHERNOUS'KO F: The optimal periodic motions of a two-mass system in a resistant medium. J. of Applied Mathematics and Mechanics 2008, 72(2):116-125.
Сергей Александрович Голованов
ФТИ им. А.Ф. Иоффе РАН, СПбПУ им. Петра Великого
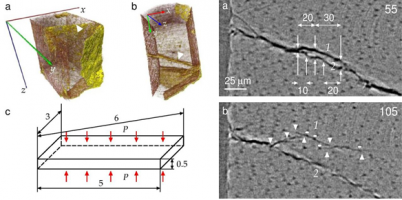
Дентин – природный пористый материал с иерархической структурой, включающей в себя не менее семи масштабных уровней. Например, дентинные каналы представляют собой вытянутые микрополости диаметром 2-5 мкм, располагающиеся на расстоянии 10 мкм друг от друга.
В течение многих десятилетий прочность и ударная вязкость дентина были в центре внимания обширных исследований, однако их происхождение до сих пор не ясно. Частично это объясняется тем, что ни один метод визуализации не может отображать по крайней мере несколько структурных уровней дентина одновременно. Среди других важных тем, связанных с дентином человека, большой интерес вызывают процессы распространения в нем трещин. Исследования в этой области показали, что основным механизмом упрочнения является перекрытие трещин связками без трещин [1]. Так называемые «мостики» неповрежденного материала наблюдались непосредственно с помощью оптического и сканирующего электронного микроскопов и рентгеновской томографии [2]. Были представлены доказательства взаимодействия каналов с растущей микротрещиной. Однако не было предложено никакого механизма, объясняющего, как образуются вторичные (сателлитные) микротрещины и как микротрещина притягивается к каналу.
В данной работе представлены экспериментальные доказательства и теоретическая модель распространения трещин поперечного сдвига в дентине при одноосном сжатии. Экспериментальные наблюдения образцов дентина размером несколько миллиметров проводились методом рентгеновской томографии с использованием синхротронного излучения. 2D-срезы (томограммы) выявили доминирующие и сателлитные трещины поперечного сдвига в образцах дентина после нагрузки: оба типа трещин распространяются по дентинным каналам [3].
Сделан вывод о том, что растягивающие напряжения на поверхности дентинных каналов, расположенных вблизи вершины заторможенной магистральной трещины, достаточны для образования сателлитных трещин. Процесс раскрытия трещины в дентине происходит за счет последовательных перемещений ее вершины от одного канала к другому (рис. 1) в плоскости действия максимальных локальных растягивающих напряжений; это сопровождается раскрытием сателлитных трещин в окрестности вершины заторможенной магистральной трещины.
Работа выполнена при поддержке гранта Российского фонда фундаментальных исследований № 19-29-12041.
1.Kinney J. H. et al. Age-related transparent root dentin: mineral concentration, crystallite size, and mechanical properties //Biomaterials. – 2005. – Т. 26. – №. 16. – С. 3363-3376.
2.Nalla R. K., Kinney J. H., Ritchie R. O. Effect of orientation on the in vitro fracture toughness of dentin: the role of toughening mechanisms //Biomaterials. – 2003. – Т. 24. – №. 22. – С. 3955-3968.
3.Argunova T. S., Gudkina Z. V., Gutkin M. Y. A Model of Microcrack Development in Human Tooth Dentin Using Data of Microtomography //Technical Physics Letters. – 2020. – Т. 46. – №. 5. – С. 505-509.
Жанна Вадимовна Гудкина