Обратная нестационарная задача о реконструкции нагрузки для модели балки Тимошенко
Автор: Яна Андреевна Вахтерова
Соавторы: Федотенков Г.В.
Организация: Московский авиационный институт (национальный исследовательский университет)
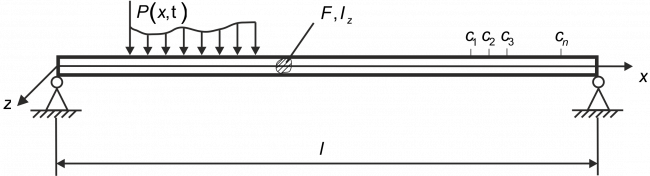
В прямоугольной декартовой системе координат рассматривается однородная изотропная балка конечной длины, исследование поперечных колебаний которой производится на основе уточненной теории, соответствующей модели С.П. Тимошенко. В качестве граничных условий используются условия шарнирного опирания. Начальные условия нулевые. В начальный момент времени к балке прикладывается распределенная нагрузка, зависящая от координаты и времени. Требуется идентифицировать нестационарную нагрузку, воздействующую на балку Тимошенко.
В основу методики решения прямой задачи положен принцип суперпозиции, при котором перемещения и контактные напряжения связаны посредством интегральных операторов по пространственной переменной и времени. При этом ядрами последних являются функции влияния для балки Тимошенко [1] (рисунок 1). Эти функции представляют собой фундаментальные решения систем дифференциальных уравнений движения исследуемой балки. Их построение представляет собой отдельную задачу. Функции влияния находятся с помощью преобразования Лапласа по времени и разложений в ряды Фурье по системе собственных функций.
Решение обратной задачи сводится к решению системы независимых интегральных уравнения Вольтера I-го рода, которая является некорректной по Ж. Адамару вследствие вырожденности ядер интегральных операторов. Для регуляризации обратной задачи применяется дифференцирование левых и правых частей уравнений, приводящие к системе интегральных уравнений с невырожденными ядрами [2].
Для решения системы разрешающих обратную задачу интегральных уравнений разработан и реализован на ЭВМ численно-аналитический алгоритм, основанный на методе средних прямоугольников.
Выполнена проверка полученных результатов. Приведены примеры расчетов.
Работа выполнена при финансовой поддержке РФФИ (проекты № 18-58-00008, 16-08-00260).
1. Горшков А.Г., Медведский А.Л., Рабинский Л.Н., Тарлаковский Д.В. Волны в сплошных средах. — М.: ФИЗМАТЛИТ, 2004. — 472 с.
2. Вахтерова Я.А., Серпичева Е. В., Федотенков Г.В. Обратная задача об идентификации нестационарной нагрузки для балки Тимошенко // Известия Тульского государственного университета. Технические науки. — 2017. — № 4. — С. 82–92.


