Одномерная задача пьезоэлектромагнитоупругой диффузии для слоя

Автор: Николай Андреевич Зверев_old

Соавторы: Земсков Андрей Владимирович, к.ф.-м.н., доцент, Тарлаковский Д.В., д.ф.-м.н., профессор

Организация: Московский авиационный институт (национальный исследовательский университет)

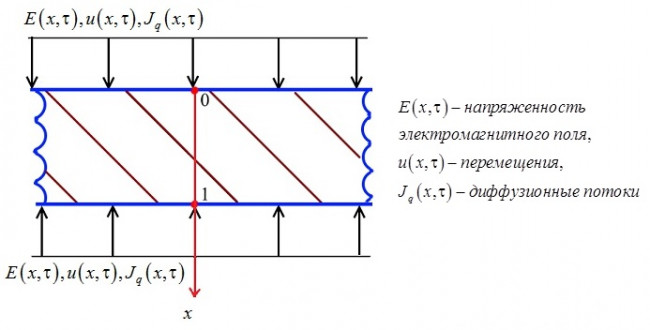
Математическая постановка задачи представляет собой связанную систему уравнений, состоящую из линейного уравнения движения сплошной среды, линейных уравнений массопереноса и уравнений Максвелла.  Физические соотношения строятся с помощью метода термодинамических потенциалов для среды с произвольной анизотропией с использованием квадратичного приближения свободной энергии как функции деформаций, изменения концентрации веществ, входящих в состав среды и компонент векторов электрической и магнитной индукций. Предполагается, что упругая среда является идеальным твердым раствором. Кроме того, прямой пьезоэлектрический, пьезомагнитный и диффузионно-электрический эффекты слабо выражены. Это позволяет рассматривать задачу электродинамики отдельно. Её решение ищется в интегральной форме, представляющей собой свертку функций Грина с правыми частями граничных условий. Для построения функций Грина задачи электродинамики используется преобразование Лапласа и разложение в тригонометрические ряды Фурье. Найденные таким образом электромагнитные поля включаются в объемные возмущения задачи упругой диффузии, решение которой известно.