Плоские контура с максимальной тягой в неизэнтропическом потоке
Автор: Альберт Ришатович Мустаев
Соавторы: Остапенко Н.А.
Организация: Научно исследовательский институт механики МГУ им. М. В. Ломоносова
Аналитически и численно поставлены и решены плоские задачи о контуре и сопле максимальной тяги в сверхзвуковом потоке с ударными волнами.
Постулируется, что оптимизируемый контур, соединяющий две заданные точки А и C, причем ХA < XC и YA < YС, состоит из двух отрезков. Первый из них прямолинейный разворачивает однородный сверхзвуковой поток, имеющий место при X=XA и Y<YA, в волне разрежения Прандтля-Майера с центром в точке А на некоторый, заранее неизвестный угол Q, разгоняя его до значительных сверхзвуковых скоростей. Второй – в общем случае криволинейный, с неизвестной формой следует за первым с изломом в точке сопряжения В, XA < XB < XC, где образуется ударная волна, повышающая давление на этом отрезке контура.
Первая из рассмотренных задач носит модельный характер и относится к оптимальному профилированию хвостовой части тела с плоской нижней (или верхней) поверхностью, не возмущающей сверхзвуковой поток. В некоторой точке А указанная поверхность терпит излом, за которым контур тела должен прийти в некоторую точку С. В соответствии с высказанным постулатом ищется контур, соединяющий точки А и С, генерирующий ударную волну в своей точке излома и доставляющий максимум функционалу тяги. Взаимодействие сверхзвукового потока за волной Прандтля-Майера со стенкой на участке ВС моделируется по формуле Ньютона. Показано, что экстремаль состоит из двух отрезков прямых, причем второй составляет с первым угол Q/2. В зависимости от числа Маха М невозмущенного потока и удлинения профилируемой кормовой части тела λ = (XC - ХA)/(YС - YA) построены области существования экстремалей, соответствующие разным Q. Установлено, что каждому углу Q в плоскости параметров (М, λ) отвечает ограниченная кривая, концы которой при λ > 0.5 соответствуют коническому профилю – отрезку прямой, соединяющему точки А и С. Между указанными точками при изменении, например, одного из параметров – числа М достигается максимум отношения Т = ТO/ТС, где ТО – тяга оптимального, ТС – тяга конического контура, в некоторых случаях превышающий единицу на несколько десятков процентов. Точное решение соответствующей оптимизационной задачи в классе отрезков прямых значительно расширяет область существования "ударных" контуров и увеличивает их преимущество по сравнению с коническими контурами.
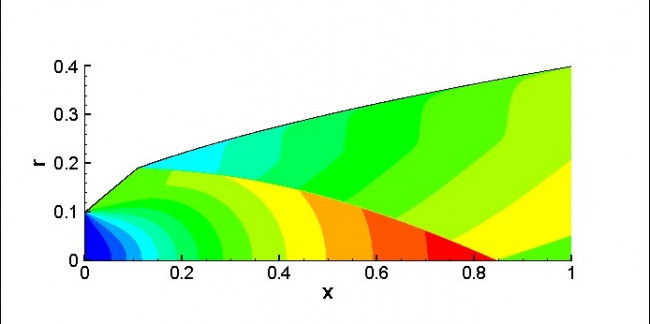
Вторая задача относится к построению плоского сверхзвукового сопла максимальной тяги с заданными координатами входа (ХA = 0, YA > 0 – критическое сечение сопла, в котором задано число Маха потока, несколько превышающее единицу: М=1.01) и выхода (XC, YС). Для приближенного определения формы экстремали на отрезке [XВ,XС] рассмотрена задача об оптимальной форме указанного отрезка при моделировании потока в сопле на отрезке [XА, XС] потоком от плоского сверхзвукового источника со звуковой линией, проходящей через точку А. Взаимодействие потока от источника со стенкой сопла на отрезке [XВ, XС] моделируется по формуле Ньютона. Показано, что каждый луч, выходящий из центра источника под некоторым углом φ ≤ Q, составляет в точке пересечения с элементарным отрезком экстремали угол φ/2. Следовательно, криволинейный отрезок экстремали является параболой, в фокусе которой располагается центр источника. С использованием построенного вычислительного кода, в котором использован метод Годунова, проведены параметрические расчеты течения в сверхзвуковой части сопла, состоящего из конического с углом Q и параболического участков, и его тяги, которая сравнивается с тягой эквивалентного конического сопла. Установлено, что в зависимости от определяющих параметров задачи тяга оптимального сопла, состоящего из прямолинейного отрезка и сопрягающегося с ним отрезка параболы, может превышать на несколько процентов тягу эквивалентного сопла с прямолинейной стенкой.
Работа выполнена при частичной финансовой поддержке РФФИ (проект № 18-01-00182).


