ПОСТРОЕНИЕ ФУНЦИОНАЛЬНО-ИНВАРИАНТНЫX РЕШЕНИЙ ДЛЯ НЕСТАЦИОНАРНОЙ КОНТАКТНОЙ ЗАДАЧИ С ПОДВИЖНЫМИ ГРАНИЦАМИ
Автор: Роман Дмитриевич Пряжевский
Соавторы: Тарлаковский Д.В., Федотенков Г.В.
Организация: Московский авиационный институт (национальный исследовательский университет), Москва
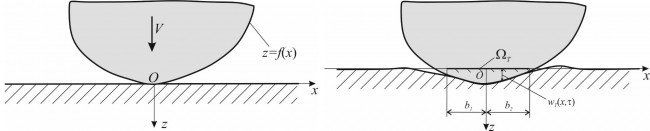
Рис. Расчетная схема внедрения.
В данной работе рассматривается плоская нестационарная задача с подвижными границами. Построено аналитическое решение на различных режимах взаимодействия посредством функционально-инвариантного метода решений. В начальный момент времени полуплоскость считается недеформированной, закон внедрения штампа -произвольный. Форма штампа является гладкой. Внутри границы области контакта перемещения полностью определяются формой ударника и законом внедрения. Напряжения вне границы полагаются равными нулю. Решение указанной задачи сводится к решению краевой задачи Гилберта [1]. При постулировании однородности функций упругих потенциалов посредством метода функционально-инвариантных решений исходная задача сводится к краевой задаче Шварца. Найдены выражения для перемещений вне контактной области и напряжений непосредственно под штампом. Как частный случай, рассмотрен случай нестационарного внедрения клина в упругое полупространство.
1. Ломунов А.К., Пряжевский Р.Д. Нестационарная контактная задача для абсолютно твердого гладкого штампа и упругой полуплоскости на дорелеевском интервале движения границ области взаимодействия. Проблемы прочности и пластичности, т. 79, № 1, С 5-15. РФФИ 16-38-50238 мол_нр, 16-08-00260 А.


