Применение метода перевала в задаче об асимптотике локализованного возмущения слоя вязкой жидкости на склоне
Автор: Юлия Сергеевна Зайко
Организация: НИИ механики МГУ имени М.В. Ломоносова
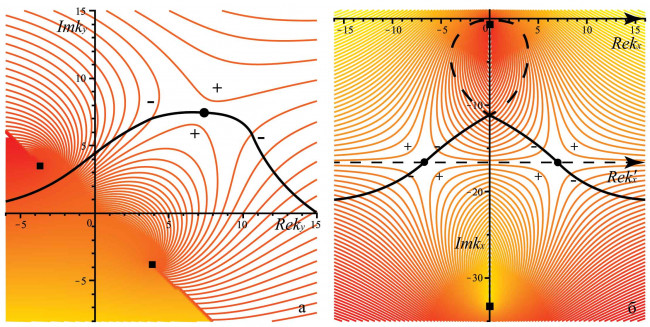
В докладе подробно описывается применение метода перевала к задаче об асимптотическом поведении локализованного возмущения потока ньютоновской среды на склоне постоянного уклона α. Движение жидкости происходит под действием силы тяжести и описывается уравнениями в гидравлическом приближении. Система уравнений имеет аналогию с системой уравнений газовой динамики, следовательно, является гиперболической. Все малые возмущения такой системы лежат внутри конуса характеристик (x-c0t)2+y2≤c02t2, который выделяет на плоскости U1,V1 круг единичного радиуса с центром в точке (q,0). Здесь U1=U/c0, V1=V/c0, q=u0/c0, x=Ut, y=Vt, u0 — модуль скорости невозмущённого течения, с0 = (ghcosα)1/2 — скорость распространения малых мелкомасштабных возмущений относительно частиц среды, оси x, y лежат в плоскости склона, невозмущённая скорость направлена вдоль оси x. С помощью метода перевала исследуется характер неустойчивости (конвективная или абсолютная неустойчивость) вдоль каждого луча x=Ut, y=Vt (U, V вещественные). В рассматриваемой задаче метод перевала применяется сначала в комплексной плоскости ky, затем в комплексной плоскости kx (возмущение считается двумерным и задаётся интегралом Фурье по всем вещественным волновым числам). С помощью метода перевала найдена форма области, занятой растущим возмущением. На рис. приведены картины линий уровня функции Im(ω(kx,ky))=const в комплексных плоскостях волновых чисел kx, ky, показаны деформированные контуры интегрирования, проходящие через перевальные точки функции ω(kx,ky) (здесь ω — комплексная частота).
Работа частично поддержана грантами РФФИ (проекты № 18-31-20057, № 18-29-10020).
