РАСЧЕТ НАПРЯЖЕНИЙ ОТ ДИЛАТАЦИОННОЙ НИТИ В УПРУГОМ КЛИНЕ
Автор: Жанна Вадимовна Гудкина
Соавторы: С.А. Красницкий, М.Ю. Гуткин, Т.С. Аргунова
Организация: ФТИ им. А.Ф. Иоффе РАН, СПбПУ им. Петра Великого
Исследование деформаций и напряжений несоответствия, связанных с полупроводниковыми наногетероструктурами сложной архитектуры, является важной проблемой материаловедения и наномеханики. Эти деформации и напряжения определяются различиями параметров решетки и коэффициентов теплового расширения контактирующих материалов, а также их химическими неоднородностями. Снижение напряжений несоответствия за счет образования различных дефектов часто сопровождается ухудшением функциональных свойств гетероструктур и их последующим разрушением. Поэтому тщательный анализ напряжений несоответствия в гетероструктурах с учетом их реальной формы огранки имеет большое значение для создания бездефектных полупроводниковых устройств с повышенными характеристиками. С этой целью мы нашли аналитическое решение краевой задачи в классической теории упругости для клиновидного тела, содержащего прямолинейную нить, подверженную трехмерному растяжению собственной деформации, которая является так называемой «дилатационной нитью».
Для определения поля напряжений этого дефекта введем функцию напряжений Эйри в виде суммы ψ = ψel + ψpl, где ψel - аналитическое решение бигармонического уравнения в упругой задаче для клина, а ψpl - частное решение, которое соответствует дилатационной нити. Интегральное преобразование Меллина используется для вывода системы уравнений для функции напряжения Эйри. В результате желаемые компоненты напряжения находятся в интегральной форме по мере обратного преобразования Лапласа-Меллина [1]. Анализ полученного решения проводился численно с использованием графиков напряжений.
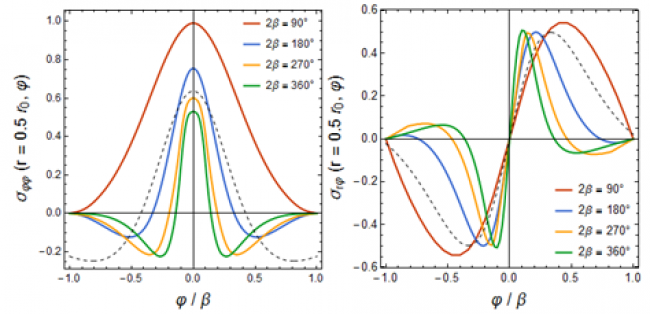
Примеры двух графиков напряжений показаны на рис. 1 для случая r = 0.5r0 и различных значений угла раскрытия клина 2β. Графики показывают, в частности, выполнение граничных условий на свободных поверхностях тела.
Найденное решение удовлетворяет уравнениям равновесия и граничным условиям на свободных поверхностях клиновидного тела. Свободные поверхности сильно влияют на распределение поля напряжений.
Работа выполнена при поддержке гранта Российского фонда фундаментальных исследований № 19-29-12041.
1.Gudkina Z. V. et al. The misfit stresses of dilatation line in semiconductor nanoheterostructures with angular boundaries //Journal of Physics: Conference Series. – IOP Publishing, 2020. – Т. 1695. – №. 1. – С. 012014.
