Существование и устойчивость пространственных колебаний в окрестности положений относительного равновесия спутника с переменным распределением масс
Автор: Анастасия Алексеевна Кириенко
Соавторы: Буров А.А, Косенко И.И.
Организация: Московский Авиационный Институт (национальный исследовательский университет)
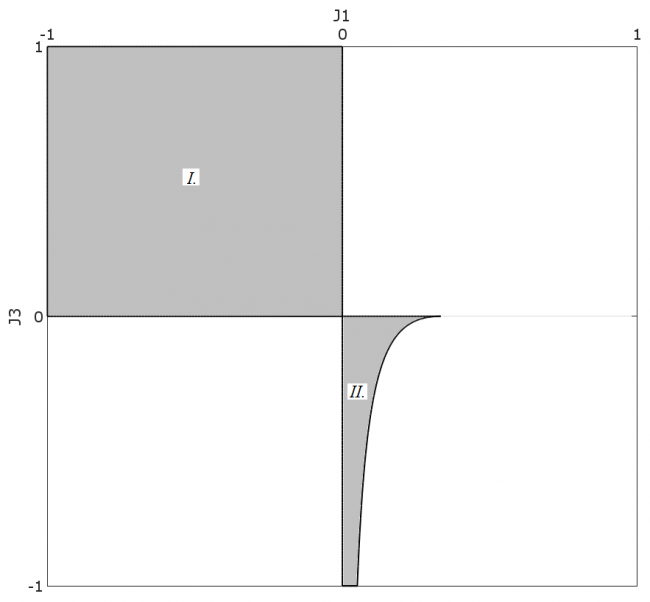
На заре изучения динамики спутников, в так называемом «спутниковом приближении», то есть в случае, когда размеры спутника значительно меньше расстояния до притягивающего центра, является частичным разделением движения: ориентационное движение спутника вокруг центра масс существенно не влияет на движение Кеплеровского центра масс спутника. В то же время движение центра масс спутника существенно влияет на изменение его положения. Использование истинной аномалии в качестве независимой переменной, вероятно, происходит на основании работы Бине, что дает возможность интегрировать задачу Кеплера и одно из двух тел. Впоследствии аналогичная переменная была применена в задаче о трех телах Леви-Чивита и Нехвилла.
Такое свойство движения центра масс, которое наблюдалось, позволило Белецкому использовать после упомянутой классики истинную аномалию в качестве независимой переменной. Было выведено так называемое «уравнение Белецкого», которое было успешно применено для описания динамических свойств движения спутника по круговой и эллиптической орбитам. Вероятно, необходимость компенсировать колебания спутника, возникающие из-за перераспределения внутренних масс, например смещения экипажа, циркуляции жидкостей, привела к идее принудительного перераспределения масс спутника в зависимости от его положения на Кеплеровской орбите. Начало исследований существования относительных равновесий спутников и их устойчивости при периодическом распределении внутренних масс было найдено в перечисленных выше работах.
В данной работе рассмотрена задача исследования динамики относительного движения спутника с переменными свойствами инерции, объектом исследования является притягивающий центр, неподвижный в пространстве со спутником с пульсирующим тензором инерции. Для решения поставленной задачи были выдвинуты основные предположения: спутниковое приближение (центр масс движется вдоль постоянной предписанной Кеплеровой орбиты) и деформация спутника таковы, что главные центральные оси инерции неподвижны относительно его «твердого» каркаса (меняться могут только величины моментов инерции). После проведения ряда вычислений были получены численные и графические решения в поставленной задаче.


