ЭКСПЕРИМЕНТАЛЬНОЕ ИССЛЕДОВАНИЕ ВЛИЯНИЯ РЕЖИМОВ ТЕЧЕНИЯ НА УСТОЙЧИВОСТЬ УПРУГОЙ ТРУБКИ
МГУ имени М.В. Ломоносова
Известно, что взаимодействие кровотока с биологическими сосудами и их возможная потеря устойчивости являются значительными проблемами в механике сердечно-сосудистой системы. В связи с этим, исследованием колебаний упругих трубок, используемых в качестве моделей сосудов, занимаются различные группы в течении десятилетий [1,2].
На данный момент существует несоответствие между большим количеством экспериментальных исследований с турбулентным течением жидкости в упругой трубке [3,4] и биомеханическими применениями, где поток в большей части сердечно-сосудистой системы ламинарный. Следовательно, изучение влияния режимов потока на возникновение и характер колебаний модельного кровеносного сосуда представляет большой интерес.
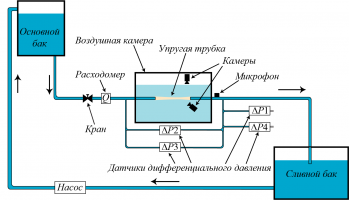
Сначала производится подбор разных жидкостей таким образом, чтобы их числа Рейнольдса соответствовали равным перепадам давления, одинаковым средним скоростям и равным трансмуральным давлениям (разность внутреннего и внешнего давлений), обеспечивающим совпадение форм трубки. В результате эти потоки будут отличаться только режимом течения, ламинарный или турбулентный. Данные потоки были организованы с использованием воды на турбулентном режиме и растворов глицерина на ламинарном режиме.
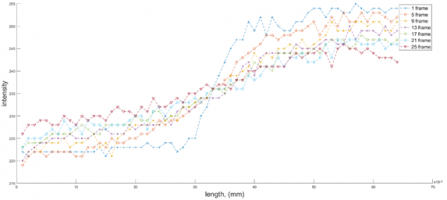
Было проведено сравнение границ устойчивости и были выявлены четыре типа колебаний, наблюдаемые по датчикам перепада давления, датчику выходного давления и визуализации режимов колебаний трубки.
1. J.B. Grotberg, O.E. Jensen. Biofluid mechanics in flexible tubes // Ann. Rev. Fluid Mech., 2004, 36, 121-147.
2. Порошина А.Б., Веденеев В.В. Существование и единственность стационарного состояния упругой трубки при протекании через нее степенной жидкости // Российский журнал биомеханики, 2018, издательство Перм. нац. исслед. политехн. ун-т (Пермь), том 22, № 2, с. 196-222.
3. Gavriely N., Shee T.R., Cugell D.W. & Grotberg J.B. Flutter in flow-limited collapsible tubes: a mechanism for generation of wheezes // J.Appl. Physiol. 1989. V. 66(5). P. 2251-2261.
4. Bertram C.D., Elliott N. S. J. Flow-Rate Limitation in a Uniform Thin-Walled Collapsible Tube, With Comparison to a Uniform Thick-Walled Tube and a Tube of Tapering Thickness // J. Fluids Struct. 2003. V. 17(4). P.541-559.