НИИ механики МГУ, Москва
Графическая аннотация – рисунок, привязанный к каждому докладу на сайте конференции, - важный визуальный элемент, разъясняющий в научно-популярном стиле суть научной работы участника конференции. Из быстрого просмотра графической аннотации на сайте конференции каждый участник нашей конференции, не специализирующийся в данной области механики, должен получить общее представление о содержании доклада. Графическая аннотация должна по возможности ответить по крайней мере на один из следующих вопросов:
- В чем заключается суть предлагаемого метода исследования некоторой научной проблемы? В чем состоит актуальность и научная новизна?
- Какова область практического приложения результатов исследований? Какая выгода от использования результатов исследований?
Если не удается подготовить графическую аннотацию, отвечающую на эти вопросы, то в качестве графической аннотации можно использовать цветной рисунок, иллюстрирующий
- результаты расчётов, излагаемых в докладе;
- постановку эксперимента;
- схему исследуемого физического явления;
- другой иллюстративный материал, который будет излагаться в докладе.
Графическая аннотация должна быть рисунком в формате JPEG или PNG, размер которого не превышает 0.5 Мб.
С графическими аннотациями конференций 2017 и 2018 годов можно ознакомиться на сайте нашей конференции.
Оргкомитет
НИИ механики МГУ, Москва
Каждому участнику конференции предоставляется возможность сделать не более одного устного доклада и 1-2 стендовых доклада. На устном докладе участник представляет основное содержание своей работы. Ожидается, что изложение устного доклада даётся в научно-популярном стиле, понятном для широкой аудитории. На стендовых докладах, дополняющих устный доклад, участник делает сообщение о частных узкоспециализированных проблемах и результатах. Продолжительность устных докладов будет определяться исходя из числа участников (но не более 20 минут). Участнику необходимо направить в адрес Оргкомитета отдельную аннотацию для каждого доклада (и устного, и стендовых).
Оргкомитет
Математический институт им. В.А. Стеклова Российской академии наук, Москва
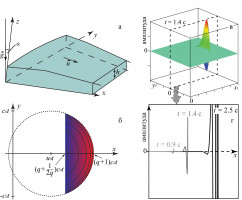
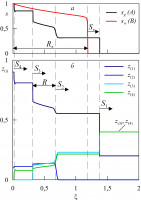
Течения потоков жидкости по наклонным поверхностям часто встречаются в природе и различных технических приложениях. С первой четверти XX века устойчивость таких потоков и развитие возмущений в них активно изучались аналитически, экспериментально, а позже и численно (см., например, [1, 2]). В настоящей работе аналитически в линейном приближении с помощью метода перевала изучается асимптотическое поведение локализованного по пространству и времени возмущения слоя линейно-вязкой жидкости на наклонной плоскости. Течение описывается уравнениями в гидравлическом приближении, то есть осреднёнными по глубине уравнениями МСС с учётом некоторых предположений (см., например, [3]). Рассматривается однородный неустойчивый поток на склоне постоянного уклона α (рис. 1а). Ранее эволюция трёхмерного локализованного возмущения открытого потока на вертикальной стенке исследовалась методом перевала в работах [2, 4]. В [2] (Глава 11, с. 327) рассматривалось течение, описываемое обобщённым уравнением Курамото-Сивашинского; в [4] — течение, описываемое системой уравнений Капицы-Шкадова.
Локализованное возмущение представляется суммой двойных интегралов Фурье, где интегрирование ведётся по всем вещественным волновым числам kx, ky (kx, ky — компоненты волнового вектора), суммирование — по корням дисперсионного уравнения (см. [5]). В начальный момент времени возмущение задаётся дельта-функцией. С помощью метода перевала определены размеры и форма области пространства, занятой растущим возмущением (рис. 1б), и поведение волны внутри этой области. (Обозначения: g — ускорение свободного падения, h — глубина потока, q = u0/c0, c0 = (gh0cosα)1/2, u0 — скорость невозмущённого потока, направленная вдоль оси x, нижний индекс «0» отмечает величины, относящиеся к невозмущённому течению.) Возмущение растёт внутри сегмента круга радиуса c0t с центром в точке x = u0t, y = 0. Гребни растущих волн — дуги окружностей с центром в той же точке (показаны серым на рис. 1б). Длина волны стремится к нулю при приближении к точке x = (q+1)c0t. Фазовая скорость возмущения превосходит групповую. Визуализация возмущения в пространстве приведена на рис. 1в.
Исследование выполнено за счет гранта Российского научного фонда (проект № 19-71-30012).
1. Алексеенко С.В., Накоряков В.Е., Покусаев Б.Г. Волновое течение пленок жидкости. — Новосибирск: ВО «Наука». Сибирская издательская фирма, 1992. — 256 с.
2. Chang H.-C., Demekhin E.A. Complex Wave Dynamics on Thin Films. D. Möbius and R. Miller. Elsevier. Amsterdam. 2002.
3. Эглит М.Э. Неустановившиеся движения в руслах и на склонах. — М.: Изд-во Моск. ун-та, 1986. — 96 с.
4. Demekhin E.A., Kalaidin E.N., Kalliadasis S., Vlaskin S.Yu. Three-dimensional localized coherent structures of surface turbulence. II. Λ solitons // Phys. Fluids. 2007. V. 19. 114104.
5. Zayko J., Eglit M. Stability of Downslope Flows to Two-Dimensional Perturbations. // Phys. Fluids. 2019. V. 31. 086601.
Юлия Сергеевна Зайко
Радиофизический факультет ННГУ имени Н.И. Лобачевского, Н. Новгород
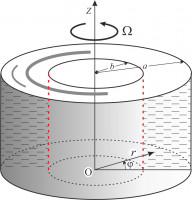
Исследуются основные свойства инерционных (гироскопических) волн во флотирующей вязкой жидкости, образующей центрифугированный слой на твердой стенке цилиндрической полости центрифуги (см. рис.). Наиболее детально рассмотрены азимутальные гироскопические волны. Флотирующая жидкость – это жидкость с инерционной поверхностью, образуемой плавающими на её свободной поверхности и не взаимодействующими между собой частицами, обладающими малой массой. Её движения описываются обычными уравнениями гидродинамики (за исключением того, что в правой части уравнения движения появляются два члена, связанные с действием кориолисовой и центробежной сил, поскольку рассмотрение ведется в неинерциальной системе отсчёта)
(1)
( – динамическая вязкость, – угловая скорость центрифуги, остальные обозначения стандартны), но граничные условия на свободной поверхности являются неклассическими
, ,
где , , , E – число Экмана, – уравнение свободной поверхности, T – вектор, определяющий реакцию частиц инерционной поверхности, в цилиндрической системе координат имеет вид
.
В отличие от традиционного подхода с применением погранслойных функций при решении задач с малым параметром при старших производных, мы ищем не приближенное, а точное решение гидродинамической задачи. Для построения решения используется суперпозиция собственных функций несамосопряженного оператора rot. Собственные вектор-функции v(x) оператора в пространстве соленоидальных полей, определяются из несамосопряженной задачи на собственные значения в двусвязной области. Получено и исследовано дисперсионное уравнение. Показано, инерционная поверхность оказывает дестабилизирующее действие. Получены оценки параметров, при которых стационарное движение жидкости является устойчивым.
Мария Андреевна Свешникова
МГУ имени М.В. Ломоносова
Гидравлическим прыжком называется резкое изменение толщины слоя жидкости, текущего по твердой поверхности, данное явление соответствует ударной волне при аналогии между течениями тонкого слоя и газовой динамикой. В настоящей работе рассматриваются круговые гидравлические прыжки, которые возникают при растекании вязкой жидкости по горизонтальному диску в радиальном направлении; струя жидкости падает в центр диска с постоянным расходом.
Рассматривается задача об определении положения гидравлического прыжка в случае, когда горизонтальная поверхность вращается. Положение прыжка определяется балансом сил инерции, трения и гидростатического давления, вращение передает дополнительные импульс жидкости за счет центробежной силы и силы Кориолиса.
Теоретическое исследование ограничено случаем стационарного осесимметричного течения. С помощью осреднения уравнений тонкого слоя с учетом вязкости, градиента гидростатического давления, центробежной и Кориолисовой сил получена система обыкновенных дифференциальных уравнений относительно толщины слоя, радиальной и окружной компоненты скорости. Проведен качественный анализ решений этой системы уравнений, получена классификация режимов течения. Получено, что при увеличении скорости вращения гидравлический прыжок смещается к периферии диска, при этом изменение толщины слоя на прыжке монотонно уменьшается до нуля. При определенной скорости вращения прыжок исчезает и решение, описывающее течение, становится непрерывным. Выявлено четыре качественно различных режима течения, которые различаются наличием и расположением зон докритического течения, где радиальная скорость течения меньше скорости распространения малых возмущений по поверхности жидкости.
Показано, что гидравлический прыжок расположен ближе к оси вращения, чем точка потери устойчивости течения по отношению к малым осесимметричным возмущениям [1].
В НИИ Механики МГУ имени М.В. Ломоносова построена экспериментальная установка для изучения подобных течений. Получено качественное соответствие между результатами расчетов и экспериментальными данными. Вместе с тем, наряду со стационарными осесимметричными режимами течения обнаружены волновые режимы (стационарные спиральные, осесимметричные капиллярные).
Работа выполнена по госбюджетному плану МГУ при частичной поддержке РФФИ (гранты 18-01-00762, 18-51-00006).
1.Могилевский Е. И., Шкадов В. Я. Течения тонких пленок вязкой жидкости по криволинейным вращающимся поверхностям // Изв. РАН. МЖГ. 2009. — № 2. — С. 18–32
Евгений Ильич Могилевский
МГУ имени М.В. Ломоносова
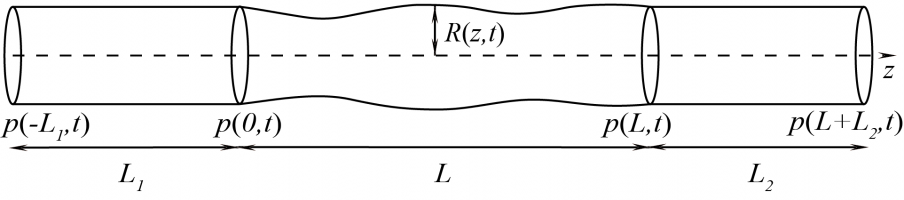
В биологических приложениях при течении жидкостей в моделях кровеносных сосудов возникают различные явления, которые оказывают влияние на характер течения и на деформацию стенок, что влечёт за собой дисфункциональные изменения в организме человека или животного.
Ранее в литературе исследовались, в основном, течения ньютоновской (линейно-вязкой) или идеальной жидкости [1, 2]. Хотя, кровь в средних и мелких сосудах обладает неньютоновскими свойствами. При этом одномерное моделирование течения крови по кровеносным сосудам является удобным инструментом для изучения динамики биологической жидкости в системе кровообращения.
Данное исследование проводилось классическими методами теории устойчивости, на основе ранее разработанной одномерной модели [3, 4]. Для трубок бесконечной длины рассматривались решения в виде бегущих волн и выводилось дисперсионное уравнение. Анализом его корней находились области неустойчивости в пространстве параметров.
Поскольку критерий устойчивости для сколь угодно большой длины трубки не совпадает с критерием устойчивости для бесконечно длинной трубки, то для определения границ устойчивости задача была исследована на нахождение области глобальной неустойчивости. В данном случае использовался асимптотический метод глобальной неустойчивости, разработанный А.Г. Куликовским [5].
Кроме того, для трубок конечной длины была решена задача на собственные значения. Граница устойчивости исследовалась численно с учетом упругости стенки трубы, продольного натяжения и длины трубки.
1.Grotberg J.B., Jensen O.E. Biofluid mechanics in flexible tubes // Ann. Rev. Fluid Mech. 2004. Vol.36. P.121–147.
2. Heil M., Hazel A.L. Fluid-Structure Interaction in Internal Physiological Flows // Ann. Rev. Fluid Mech. 2011. Vol.43. P.141–162.
3. Порошина А.Б., Веденеев В.В. Существование и единственность стационарного состояния упругой трубки при протекании через нее степенной жидкости // Российский журнал биомеханики. 2018. Т. 22. № 2. С. 196–222.
4. Веденеев В.В., Порошина А.Б. Устойчивость упругой трубки, содержащей текущую неньютоновскую жидкость и имеющей локально ослабленный участок // Труды МИАН. 2018.
Т. 300. С. 42–64.
5. Куликовский А.Г. Об устойчивости однородных состояний // Известия АН СССР. ПММ. 1966. Т. 30. Вып. 1. С. 148-153.
Анастасия Борисовна Подопросветова
Московский государственный университет имени М.В.Ломоносова
Потоки на склонах, такие как снежные лавины, грязекаменные сели, оползни, подводные мутьевые потоки, в процессе движения разрушают подстилающую поверхность и уносят массу вниз по течению. В случае селевых или подводных мутьевых потоков интерес представляет глубина разрушения склона, так как потоком могут быть разрушены элементы инфраструктуры, изменена форма русла. В случае снежных лавин разрушение подстилающей поверхности изучается для определения изменения массы потока, так как в процессе движения масса потока может измениться в несколько раз, это важно учитывать при проектировании заградительных сооружений.
Для моделирования разрушения потоком и вовлечения в движение материала склона используется многофазный подход. Методом контрольных объёмов рассчитывается движение 3 фаз: материал подстилающей поверхности, материал движущегося потока, воздух. Используется решатель multiphaseInterFoam пакета OpenFOAM. В качестве механизма захвата рассматривается захват при превышении напряжения на дне потока некоторого порогового значения, описанный в работах [1, 2]. Материал потока представлен средой Хершеля-Балкли, использование данного реологического закона позволяет смоделировать процесс отложения материала потока на поверхности склона, а также остановку потока.
Для верификации полученной модели течения рассчитывается снежная лавина в 22 очаге на горе Юкспор (Хибины). Последний раз катастрофическая лавина сошла здесь в 2017 году, тогда были засыпаны автомобильная и железная дороги, выбиты окна в близлежащем доме, погибли 3 человека. В работе используются данные о лавине из этого очага, сошедшей в 1965 году. Для этой лавины известна масса сорвавшегося снега и масса лавинных отложений, что позволяет оценить количество захваченного потоком материала.
Дарья Игоревна Романова
НИИ механики МГУ им. М.В. Ломоносова
Исследуется эффективность газового воздействия на нефтяной пласт, в рамках моделирования смешивающегося вытеснения в пористой среде при закачке углеводородного (УВ) газа. Для описания течения в пористой среде, используется композиционная модель фильтрации, позволяющая учесть изменения компонентного состава жидкостей и газов в пласте, теплофизические свойства которых задаются уравнением состояния Ван-дер-Ваальсового типа. Эффективность нефтеотдачи сравнивается с получаемой при применении традиционной технологии заводнения. Для проведения исследований разрабатывающийся авторами комплекс программ MUFITS [1,2] дополнен модулем для композиционного моделирования фильтрации. На данном примере демонстрируются его обновленные функциональные возможности.
В модели учитывается, что в зависимости от давления и температуры УВ смесь находится либо в однофазном состоянии газа или жидкости (нефти), либо в двухфазном состоянии газ–нефть. Вода же не смешивается с УВ, образуя отдельную компоненту жидкости. Давление во всех фазах считается одинаковым – капиллярное давление пренебрежимо мало, изменение температуры – тоже. Течение происходит в тонком горизонтальном пласте, влиянием силы тяжести пренебрегается.
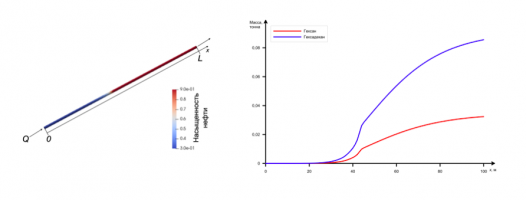
Рассматриваются модельные составы нефти и вытесняющего газа, совпадающие с одними из предложенных в [3] – случай A. По постановке задача является автомодельной задачей Римана. Её решение состоит из последовательности сильных разрывов (S), на которых рвутся распределения насыщенностей газа sg и воды sw, полные концентрации компонент смеси zi; центрированных волн Римана (R) и областей однородного распределения параметров, распространяющихся от входной границы внутрь области (S4-S3RS2-S1). В случае B в пласт закачивается вода, а решение содержит только один разрыв и одну волну Римана (R*S*) – случай B. Результаты численного моделирования приведены на рис. (рис. Распределения насыщенностей газа и воды в случаях А и B (а) и полных мольных концентраций в задаче А (б), соответственно.)
Исследованы характерные времена, на которых закачка газа позволяет извлечь наиболее ценные УВ компоненты нефти. Показано, что закачка воды в целом более эффективный метод повышения нефтеотдачи из пластов, насыщенных нефтью рассмотренного модельного состава. Газовое воздействие позволяет извлечь дополнительное количество промежуточных компонент УВ ряда только после закачки 3 поровых объемов газа. Однако, это дополнительное количество мало и, по-видимому, не имеет практической значимости. Еще меньший эффект достигается при вытеснении тяжелых компонент.
1. Afanasyev A.A. Hydrodynamic modelling of petroleum reservoirs using simulator MUFITS// Energy Procedia. 2015. V. 76. P. 427–435.
2. Afanasyev A., Kempka T., Kühn M., Melnik O. Validation of the MUFITS reservoir simulator against standard CO2 storage benchmarks and history-matched models of the Ketzin pilot site // Energy Procedia. 2016. V. 97. P. 395–402.
3. Orr F.M. Theory of gas injection processes. Holte, Denmark: Tie-Line Publications, 2007. 381 p.
Елена Анатольевна Веденеева
ИПФ РАН
Морской аэрозоль в приповерхностном слое играет огромную роль в процессах обмена импульсом, теплом и газообмена. В настоящий момент мелкомасштабные быстропротекающие процессы обуславливающие механизмы образования брызг при ветро-волновом взаимодействии изучены слабо. В натурных условиях это сделать практически невозможно, поэтому прибегают к моделированию на крупномасштабных ветро-волновых каналах. При этом наиболее перспективными методом регистрации событий представляется высокоскоростная видеосъемка со специальной визуализацией.
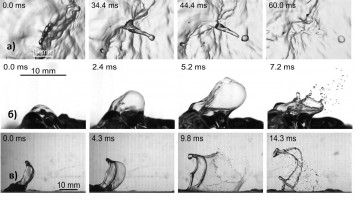
В настоящей работе приведены исследования, выполненные на Ветро-Волновом Термостратифицированном бассейне (ВВТСБ) ИПФ РАН [1]. С помощью высокоскоростной видеосъемки и теневой подсветки были получены изображения, характеризующие процессы образования брызг. Теневые фотографии типичных событий, приводящих к генерации капель, показаны на Рис. 1 (а-в). Мможно предложить их следующую классификацию:
1. Дробление жидких "пальцев" (Рис. 1а). В районе гребней обрушающихся волн развиваются небольшие выступы воды, которые затем растягиваются в «пальцы» и разрываются на одну-две капли диаметрами несколько миллиметров.
2. Разрыв подводных пузырей (Рис. 1б). Подводные пузыри, формирующиеся у гребней обрушающихся волн, всплывают из-за положительной плавучести и разрываются при достижении поверхности воды, генерируя брызги.
3. Дробление типа "парашют" (Рис. 1в). Это явление начинается с появления мелкомасштабного возвышения водной поверхности, затем развивающегося в «микро-парус», который раздувается разрывается, образуя сотни брызг.

Рис. 1. Фотографии событий, сопровождающих генерацию брызг: а) дробление жидких "пальцев" (вид сверху); б) разрыв подводных пузырей (вид сбоку); в) нижний ряд фотографий – формирование и разрыв «парашюта» (вид сбоку)
Максим Игоревич Вдовин
Центральный аэрогидродинамический институт им. проф. Н.Е. Жуковского, Московский государственый университет имени М.В. Ломоносова

Использование гидрофобных покрытий представляет интерес в широкой области технических и бытовых приложений, в частности в задачах противодействия обледенению летательных аппаратов. Гидрофобные поверхности обладают своеобразными функциональными свойствами, к которым следует отнести водонепроницаемость, стойкость к коррозии, устойчивость к биообрастанию, к неорганическим, а в ряде случаев и к органическим загрязнениям. Благодаря многообразию управляемых свойств создание гидрофобных тел в настоящее время интенсивно развивается. Такие покрытия, как правило, эффективно работают при незначительных числах Вебера, рассчитанных по характерным размерам H рельефа поверхности We = HρV2/σ, (ρ – плотность жидкости, σ – коэффициент поверхностного натяжения, V – скорость удара капли). Однако при превышении поверхностной плотности кинетической энергии (переохлаждённой капли) некого критического значения, льдофобные свойства приводят к отрицательным эффектам ввиду проникновения жидкости в углубления и застывания в них. В случае динамического воздействия свойства гидрофобных/льдофобных покрытий определяются коэффициентами отскока капель в зависимости от числа Вебера. Достоверность полученных результатов обоснована сравнением с теоретическими и экспериментальными оценками других исследователей. Проведены параметрические исследования прилипания жидкости к рельефным покрытиям твердого тела, которые сформированы из комбинации гидрофобных и льдофобных материалов.
Иван Алексеевич Амелюшкин
НИИ механики МГУ, Москва
Рассматривается закачка смесей воды, углекислого газа, метана и пропана в геологический пласт, насыщенный нефтью. Исследуется в каком порядке и в течение каких интервалов времени нужно закачивать указанные газы и воду для максимального вытеснения наиболее ценных бензиновых фракций нефти.
Оптимальные режимы закачки газов исследуются в рамках одномерной постановки задачи. Предполагается, что при пласт насыщен нефтью заданного состава. При через границу закачивается вода, углекислый газ, метан и пропан с заданным объёмным расходом , а нефть, таким образом, вытесняется через границу . Определяются составы газов, позволяющие максимизировать для данного момента времени вытеснение наиболее ценных компонент углеводородного ряда. Для определения оптимального состава вытесняющей смеси сначала рассматривается закачка каждого вещества по отдельности, а затем – их смеси. Показано, что вода – более эффективный вытесняющий агент на начальном этапе закачки, однако ряд газов (как, например, CO2) оказываются более эффективными на поздних этапах. Проведены оптимизационные расчеты, позволившие определить наиболее эффективные смеси на различных этапах разработки месторождений.
Для практики представляет интерес вытеснение более тяжелых компонент нефти бензиновой и лигроиновой фракции, использующихся при производстве топлив. Первый рассмотренный состав нефти содержит пентан (C5H12) и пентадекан (C15H32), а второй – гексан (C6H14) и гексадекан (C16H34). Для первого состава была рассмотрена закачка воды, углекислого газа и метана, а во втором случае к этому составу был добавлен пропан. В зависимости от количества закачиваемых поровых объёмов получен оптимальный состав закачиваемого вещества. Отметим, что для второго состава нефти оптимальным оказался состав закачиваемого вещества, не содержащий углекислого газа.
Анна Александровна Чернова
НИИ Механики МГУ
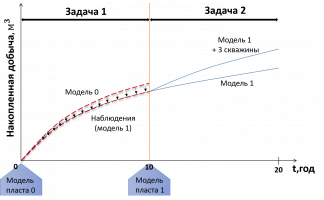
При разработке нефтяных месторождений часто необходимо определять параметры подземных пластов по измеряемым параметрам в скважинах и оптимизировать саму разработку месторождений. Для этого необходимо решать, в частности, обратные задачи, позволяющие найти неизвестные параметры гидродинамических моделей пластов при помощи их калибровки (адаптации) к наблюдаемым данным. Рассмотрим эту проблему на примере двух задач: 1) определение проницаемости пласта по забойному давлению и измерению расхода нефти через скважины и 2) определение оптимальной расстановки скважин, позволяющей максимизировать добычу нефти в течение заданного интервала времени.
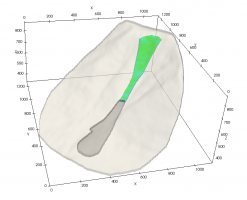
Эффективность предлагаемого метода оценивается на примере трехмерной синтетической модели нефтяного месторождения – пласта, состоящего из 3-х более тонких пропластков, которые могут быть насыщенны водой и нефтью. На этом месторождении установлены 6 добывающих скважин. Данная гидродинамическая модель пласта (модель 0) построена в момент времени t=0 лет, в течение 10 лет велась разработка месторождения (рис.). В момент времени t=10 лет (настоящее время) замечено, что данные наблюдений не совпадают с данными модели 0. С помощью метода оптимизации была проведена корректировка модели (модель 1) – уточнения значений проницаемостей пластов. Для увеличения добычи нефти в течение последующих 10 лет, используя скорректированную модель 1, расставляются 3 нагнетающие скважины оптимальным образом так, чтобы добыча была максимальной. Таким образом, была увеличена добыча нефти на 7% по сравнению с тем, если бы разработка велась бы все 20 лет без нагнетающих скважин.
Анна Игоревна Андреева
НИИ механики МГУ
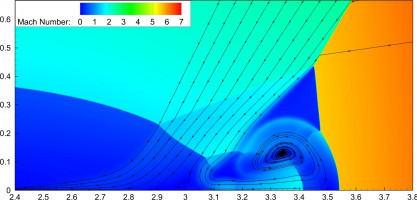
В работе исследуется структура автомодельного течения при отрицательном маховском отражении ударных волн от клина - когда падающая и отраженная ударные волны расположены по разные стороны от прямолинейной траектории движения тройной точки [1]. Такие режимы для умеренных значений числа Маха реализуются в газах с показателем адиабаты, близким к единице (в экспериментах – для тяжелых газов со сложной молекулярной структурой).
Численное моделирование в рамках уравнений Эйлера для нестационарных двумерных течений идеального газа выполнено с использованием TVD модификации явной конечно-разностной схемы с использованием сквозного метода расчета газодинамических разрывов. Для аналитического исследования полученного численного решения применены метод замороженной системы координат, связанной с набегающей ударной волной (автомодельное поле скоростей) [2], который позволяет построить линии тока в каждой точке пространства и метод ударных поляр.
Изучено поведение маховских конфигураций при приближении к критическому значению угла клина в области перехода к регулярному отражению. Исследовано влияние различных неоднородностей и препятствий вблизи поверхности клина на устойчивость режима многократного маховского отражения.
Андрей Николаевич Максимов
НИИ механики МГУ им. М.В. Ломоносова, Институт теории прогноза землетрясений и математической геофизики РАН
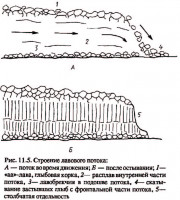
Лавовые потоки зачастую движутся по уже извергнутому ранее материалу, на их поверхности за счет остывания может образовываться «корка», которая растрескивается и обрушивается перед потоком. В результате, в застывших потоках наблюдается подслой в виде лавобрекчии – породы, представляющей собой обломки лавы, ей же сцементированные [1], см. рис. При движении этот подслой, содержащий значительную долю обломков остывшей породы, в значительной мере не сцеплен с подстилающей поверхностью. В простейшей постановке это явление было учтено в рамках осесимметричной модели растекания лавы [2].
Трещинные вулканы, или линейные вулканы, характеризуются тем, что излияние лавы на земную поверхность происходит по протяженным трещинам, они могут иметь вид цепи конусов. Извержения происходят вдоль всей трещины или в отдельных её частях.
В настоящей работе в плоской двумерной постановке рассматривается задача о растекании лавы как несжимаемой неньютоновской жидкости по плоской наклонной подстилающей поверхности – склону от точечного источника. На поверхности ставится обобщенное условие Навье – скорость на поверхности считается степенной функцией трения. Аналогично [2], в приближении тонкого слоя задача сводится к решению одного нелинейного дифференциального уравнения в частных производных второго порядка с интегральным условием. При существенном ограничении на параметры задачи найдено автомодельное решение, в общем случае решение строится численно. Рассматривается влияние параметров задачи на скорость распространения лавовых потоков и их толщину.
Решение такой модельной задачи о течении вязкой жидкости с частичным проскальзыванием представляет интерес не только с точки зрения рассматриваемой проблемы. Частичное проскальзывание встречается для неньютоновских жидкостей, представляющих собой многокомпонентные системы, таких как концентрированные суспензии, эмульсии, гели и т.п., вязкие жидкости проскальзывают вдоль супергидрофобных поверхностей – см., например, [3].
1. Короновский Н. В., Якушова А. Ф. Основы геологии: Учеб. для географ. спец. вузов. М.: Высш.шк., 1991. 416 с.
2. Веденеева Е. А. Растекание лавы во время вулканических извержений при условии частичного проскальзывания на подстилающей поверхности // Изв. РАН. МЖГ. 2015. № 2. C. 27-40.
3. Malkin A. Ya., Patlazhan S. A. Wall slip for complex liquids – Phenomenon and its causes // Advances in Colloid and Interface Science. 2018. V. 257. P. 42-57.
Елена Анатольевна Веденеева
ИФТТ РАН, ИТФ РАН
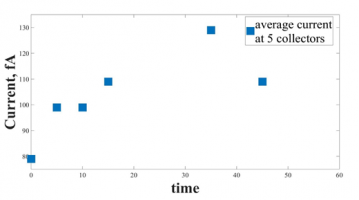
На рисунке: Зависимость суммарного тока от времени. Usours=350В,Uside1=6В,Uside2=6В,Uup=5В,Udown=25В, Freq=13Гц,A=10В
Вихревое движение может быть создано волнами на поверхности жидкости. При движении двух неколлинеарных волн под углом друг к другу формируется решетка вихрей.[1] Первоначально эксперименты по генерации вихрей волнами проводились на воде. Однако в природе, помимо классических жидкостей, существуют и квантовые жидкости, в которых вихревое движение квантовано. К таким жидкостям относится гелий-4 при температуре ниже 2,17 К. При температурах около 1,3 К плотность сверхтекучей компоненты доминирует. Инжектированные заряды являются хорошими пробными частицами для изучения вихревых течений в сверхтекучей жидкости, поскольку они взаимодействуют с квантовыми и нормальными вихрями[2].
Основной целью данной работы является изучение формирования квантовых вихревых структур поверхностными волнами в широком диапазоне температур, а также изучение эволюции вихревых структур при изменении условий накачки волн. Исследования проводились в гелиевой ячейке, находящейся в гелиевом криостате. В ходе эксперимента измерялся ток, приходящий на сборный коллектор. Волны на поверхности возбуждались двумя перпендикулярными плунжерами.
Чтобы оценить поведение вихревой структуры после отключения накачки, мы измерили временную зависимость величины общего тока, поступающего на все 5 сегментов. Точки на рисунке демонстрируют результаты измерений, выполненных через 0, 5, 10, 15, 35, 45 минут после выключения откачки. Видно, что суммарный ток линейно увеличивается со временем примерно на 30%. Можно предположить, что доля зарядов не достигла коллекторов из-за взаимодействия с вихрями. По-видимому, в результате взаимодействия заряды могут отклоняться от прямой траектории и перемещаться к боковым граням.
Разработан метод исследования поведения вихревой системы в сверхтекучем гелии-4 с помощью инжектированных зарядов. Первые эксперименты показывают, что волны на поверхности сверхтекучего гелия генерируют вихри, которые проникают в объем. В будущих экспериментах мы планируем более детально изучить взаимодействие зарядов с квантовыми вихрями.
Работа выполнена при поддержке гранта Министерства науки и высшего образования РФ #075-15-2019-1893
1. S.V. Filatov, V.M. Parfenyev, S.S. Vergeles, M.Y. Brazhnikov, A.A. Levchenko, V.V. Lebedev // Physical Review Letters. – 2016. – V. 116. – I. 5. – P. 054501.
2. P. M. Walmsley, A. I. Golov, H. E. Hall, A. A. Levchenko, and W. F. Vinen, PRL 99, 265302 (2007)
Мадина Рафаиловна Султанова