НИИ механики МГУ имени М.В. Ломоносова
При моделировании течений смеси газ-частицы необходимо задавать начальное распределение частиц на плоскости (в пространстве). При этом частицы должны быть расположены достаточно равномерно, но хаотично – иначе влияние начального распределения частиц на течение смеси может быть существенно.
В [1] предложен метод равномерного заполнения n-мерного пространства одинаковыми частицами (заданный одним параметром – желаемым расстоянием между центрами частиц). В этой работе на основе метода, предложенного в [1], строится метод равномерного заполнения области на плоскости (в пространстве) частицами разного размера (двух различных диаметров). Исследуется зависимость получаемой в результате концентрации частиц от заданного расстояния между частицами (параметра метода). В результате решается обратная задача построения равномерного распределения частиц двух разных диаметров на плоскости (в пространстве) в зависимости от заданной концентрации частиц и доли крупных частиц.
Работа выполнена при поддержке гранта РФФИ 16-05-00004 А
1. Robert Bridson. Fast Poisson Disk Sampling in Arbitrary Dimensions // ACM SIGGRAPH. 2007. Article No. 22. DOI: 10.1145/1278780.1278807
Наталья Владимировна Горохова
НИИ механики МГУ, Москва
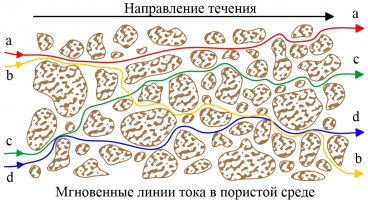
Многокомпонентные течения жидкостей и газов в пористых средах сопровождаются перемешиванием, приводящим к выравниванию полей концентрации – компонентного состава жидкости. К перешиванию приводит, во-первых, молекулярная диффузия, вызывающая перенос компонента жидкости в направлении противоположном градиенту его концентрации. Вторым механизмом перемешивания является механическая дисперсия в пористой среде, связанная с переменчивостью на масштабе отдельных пор поля скорости жидкости и соответствующим ветвлением траекторий движения элементарных частиц (Рис.) [1,2]. Интенсивность перемешивания из-за механической дисперсии зависит от направления и абсолютной величины средней скорости жидкости. В направлении, совпадающим с вектором средней скорости, интенсивность определяется различной скоростью движения частиц вдоль различных траекторий, а в перпендикулярном направлении – частотой ветвления траекторий. Во многих приложениях, как, например, при развитии слоистой конвекции в неизотермических фильтрационных течениях солёной воды, интенсивность перемешивания из-за механической дисперсии может на несколько порядков превышать интенсивность молекулярной диффузии.
В настоящей работе проведено расширение функциональных возможностей комплекса программ MUFITS [3] для численного моделирования неизотермических многокомпонентных многофазных течений в пористой среде. Разработан новый модуль для расчёта однофазной фильтрации с учётом механической дисперсий. Тестирование методов расчёта механической дисперсии, реализованных в модуле, проведено на одномерных и двухмерных задачах двухкомпонентной фильтрации соленой воды, допускающих аналитическое решение. Получены оценки для размеров шагов сетки по пространству и времени, при которых механическая дисперсия на порядок величины превосходит численную дисперсию. Обсуждаются особенности применения разработанного модуля к расчёту слоистой конвекции в пористой среде. Даны оценки скорости перемешивания из-за молекулярной диффузии и механической дисперсии при развитии конвекции.
Работа выполнена при финансовой поддержке РНФ (грант № 16-17-10199).
Рисунок: Схематическое изображение процесса механической дисперсии в пористой среде. В установившемся «осредненном» течении частицы жидкости, выпущенные в различные моменты времени из одно и той же точки (a/b; c/d), перемещаются вдоль различных траекторий.
1. Whitaker S. Diffusion and dispersion in porous media// AIChE J. 1967. V.13. P.420–427.
2.Sahimi M., et al. Dispersion in flow through porous media – I. One-phase flow// Chem. Eng. Sci. 1986. V.41(8). P.2103–2122.
3. Afanasyev A. MUFITS Reservoir Simulation Software. http://www.mufits.imec.msu.ru/
Андрей Александрович Афанасьев
Волгоградский государственный технический университет
Одной из актуальных проблем развития современных транспортных средств, в том числе шагающих машин и роботов, является проблема интеллектуализации систем управления ими.
Принимается гипотеза о том, что реализуемые системой управления роботом законы являются оптимальными по тому или иному комплексному критерию оптимальности. Для удобства интерпретации человеком этих показателей и взаимодействия человека и робота их удобно сопоставлять с чертами характера человека и представлять как набор нечётко-логических описаний динамических характеристик робота.
Ярослав Владимирович Калинин
ФИАН им. П.Н. Лебедева
Рассматриваются свойства симметричной части тензора градиентов скорости, называемого тензором скоростей деформации, в развитом турбулентном потоке несжимаемой жидкости. На основании анализа численных данных [1, 2] обнаружена симметрия распределения тензора в однородном изотропном турбулентном потоке. Аналогичная симметрия получена аналитически для случая гауссового распределения скоростей [3].
Используя аналитическое выражение симметрии удается показать, что функция распределения нормированного собственного значения тензора [4, 5] имеет универсальный характер в обоих случаях.
Показано, что искажение симметрии распределения для малоинтенсивных пульсаций может быть связано с влиянием гауссовой крупномасштабной силы (или иного стохастического источника, поддерживающего стационарность потока), поскольку имеет ярко выраженный гауссов характер.
Исследование выполнено во ФГУП «Центральный аэрогидродинамический институт имени профессора Н.Е. Жуковского» за счет гранта Российского научного фонда (проект №17-11-01271)
1. Perlman E., Burns R., Li Y., Meneveau C. Data Exploration of Turbulence Simulations using a Database Cluster // Supercomputing SC07, ACM, IEEE., 2007.
2. Li Y., Perlman E., Wan M., Yang Y., Burns R., Meneveau C., Burns R., Chen S., Szalay A., Eyink. G. A public turbulence database cluster and applications to study Lagrangian evolution of velocity increments in turbulence // Journal of Turbulence, 2008, т. 9, № 31.
3. Kopyev A. V. Degeneracy of velocity strain-rate tensor statistics in random isotropic incompressible flows // Phys. Rev. Fluids, 2018, т. 3, 024603.
4. Kerr R. M. Histograms of helicity and strain in numerical turbulence // Phys. Rev. Lett., 1987, т. 59, № 7, 783-786.
5. Lund T. S., Rogers M. M., An improved measure of strain state probability in turbulent flows // Phys. Fluids, 1994, т. 6, № 5, 1839-1847.
Алексей Викторович Копьев
ФИАН им. П.Н. Лебедева

Известно, что турбулентность характеризуется перемежаемостью, что проявляется, в частности, в развитии неизотропных нестационарных интенсивных мелкомасштабных вихревых структур [1]. В работе показано, что исходя из общих уравнений динамики жидкости, можно дать количественные оценки явлению раскручивания и вытягивания небольших жидких частиц из инерционного интервала изотропной турбулентности. Само явление, названное ранее пируэт-эффектом [2], раскрывает механизм образования интенсивных структур в мелкомасштабной турбулентности. На основании [3] в работе построена линейная стохастическая лагранжева модель, в которой получено кинетическое уравнение на функцию распределения квадрата косинуса угла между завихренностью и собственным вектором тензора скоростей деформации жидкой частицы, а также аналитически посчитаны асимптотики зависимости от времени этой величины при больших и малых временах [4]. Результаты находятся в хорошем согласии с результатами проведенных ранее экспериментов и численных расчетов [2, 5]. Проведенный анализ показывает, что линейные процессы, возможно, играют основную роль в некоторых процессах принципиально нелинейного явления изотропной турбулентности.
Важность представленных результатов заключается в самом факте применимости линейной стохастической модели в принципиально нелинейном процессе турбулентности. Показано, что линейные эффекты возможно играют главную роль в пируэт-эффекте, который раскрывает механизм образования интенсивных вихревых структур в мелкомасштабной турбулентности.
Исследование выполнено во ФГУП «Центральный аэрогидродинамический институт имени профессора Н.Е. Жуковского» за счет гранта Российского научного фонда (проект №17-11-01271)
1. Кузнецов В.Р., Сабельников В.А. Турбулентность и горение, М: Наука, 1986, 288 с.
2. Xu H., Pumir A., Bodenschatz E. The pirouette effect in turbulent flows // Nat. Phys., 2011, 7, 709.
3. Зыбин К.П., Сирота В.А., Ильин А.С., Гуревич А.В. Генерация мелкомасштабных структур в развитой турбулентности // ЖЭТФ, 2007, 132, 2 (8), 510-523.
4. Зыбин К.П., Копьев А.В. Теоретическая модель возникновения вихревых структур в изотропном турбулентном потоке, основанная на линейном механизме // Изв. РАН. МЖГ, 2018, 4, в печати.
5. Pumir A., Bodenschatz E., Xu H. Tetrahedron deformation and alignment of perceived vorticity and strain in a turbulent flow // Phys. Fluids, 2013, 25, 035101
Алексей Викторович Копьев
Объединенный институт высоких температур Российской академии наук, Москва
Неустойчивость фронта пламени – одна из актуальных задач современной механики жидкости и газа. В зависимости от процессов, определяющих рост неоднородностей, для свободного сферического пламени различают гидродинамическую (Дарье-Ландау), термодиффузионную и неустойчивость Рэлея-Тейлора. Условиям для развития последней и посвящена данная работа.
Неустойчивость Рэлея-Тейлора возникает на границе раздела двух жидкостей или газов разной плотности при наличии ускорения, направленного от более легкого к тяжелому. При распространении пламени менее плотные разогретые продукты горения двигаются с ускорением в более плотном газе. Когда вектор ускорения и градиент плотности на фронте пламени сонаправлены, происходит развитие неустойчивости. Основным параметром, определяющим скорость развития этой неустойчивости, является число Атвуда. В ходе работы было рассчитано число Атвуда и обнаружено, что на границе раздела продуктов сгорания и горючей смеси оно зависит от начального содержания водорода.
Для исследования развития неустойчивостей была проведена серия экспериментов. Прозрачные латексные оболочки наполнялись предварительно подготовленной водородно-воздушной смесью. В различных сериях экспериментов менялось процентное содержание водорода. Инициирование пламени производилось искровым разрядом с энергией 1мДж, разрядником, расположенным в центре оболочки. Регистрация распространения фронта пламени производилось с использованием теневого метода реализованного в теневом приборе ИАБ-451 и высокоскоростной камеры ВидеоСпринт. Видеосъемка процесса производилась с частотой от 500 до 1000 кадров в секунду с экспозицией в 500 мкс. С целью автоматизации обработки полученных изображений в среде Matlab написана программа, преобразовывающая набор изображений расширяющегося фронта пламени в зависимость среднего радиуса от времени.
Обнаружено, что на начальной стадии распространения возникают как ускорения, так и замедления фронта пламени. Экспериментально полученные параметры распространения фронта пламени дополнены расчетами, проведенными по аналитической модели из литературы.
Работа выполнена при поддержке Российского Научного Фонда, грант №14-50-00124.
Артём Евгеньевич Ельянов
Пермский Национальный Исследовательский Политехнический Университет
При определении усилий в жевательных мышцах и в ВНЧС имеет место проблема статической неопределимости: в общем случае имеется шесть уравнений равновесия при порядка двадцати неизвестных усилиях.
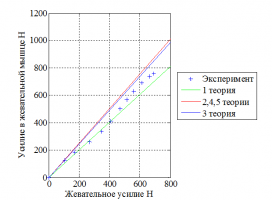
Сравнивается пять способов теоретического определения усилий в жевательных мышцах и реакции в височно-нижнечелюстном суставе (ВНЧС) с помощью упрощённой симметричной модели Канга [1]. Упрощённая модель предполагает определение только основных мышечных усилий: усилия в височной мышце и суммарного усилия жевательной и внутренней крыловидной мышц, а также величины и направления реакции ВНЧС. Рассматривалось два варианта упрощённой модели – без учёта действия мышц-открывателей и наружной крыловидной мышцы [1] и с их учётом. Для раскрытия статической неопределённости использовались пять теорий, основанных на следующих предположениях: 1) мышцы-синергисты функционально равноправны; 2) усилия в мышцах пропорциональны площадям их поперечных сечений; 3) усилия в жевательных мышцах должны обеспечивать минимальное значение реакции в суставе; 4) усилия в жевательных мышцах должны быть таковы, чтобы максимальное по мышцам напряжение было минимально возможным; 5) усилия в жевательных мышцах должны быть таковы, чтобы максимальное по мышцам отношение усилия к его максимальному значению было минимально возможным.
Показана эквивалентность 2, 4 и 5 теорий в рамках используемой упрощённой модели. Показана необходимость учёта мышц-открывателей и наружной крыловидной мышцы. Сравнение результатов расчётов по различным теориям с экспериментальными данными Пруима [2] показали, что предложенная в работе [3] теория, основанная на предположении о функциональной равноправности мышц-синергистов, является предпочтительной (рис.1).
Савелий Евгеньевич Пешин
НИИ механики МГУ
Было создано компактное устройство, формирующее воздушную струю диаметром 0.12 м, которая остается ламинарной на расстоянии 5.5 диаметров от выхода из формирующего устройства при числах Рейнольдса около 10000 [1].
Первым этапом настоящей работы является теоретическое исследование развития малых возмущений в струе с профилями скорости, соответствующими экспериментальным в начальном сечении струи и нескольких сечениях, близких к началу струи. Пространственный анализ устойчивости показал, что существует две ветви растущих возмущений: первая ветвь порождается точками перегиба на профилях скорости, расположенными вблизи границы струи; вторая — точкой перегиба, расположенной недалеко от оси струи. При этом скорости роста возмущений, соответствующих первой ветви, значительно больше скоростей роста возмущений, соответствующих второй ветви. Однако, с удалением от выхода из формирующего устройства, возмущения, соответствующие первой ветви, становятся затухающими (происходит слияние двух точек перегиба на профиле скорости в одну). Тогда неустойчивость продолжает порождаться только второй ветвью. Диапазон частот растущих возмущений для обеих ветвей одинаков и соответствует частотам 0…14 Гц. Частоты наиболее быстро растущих возмущений для обеих ветвей также лежат в одинаковом интервале — от 4 до 6 Гц.
Достаточно большой диаметр и длинный ламинарный участок струи, создаваемой экспериментально, позволяют детально измерять характеристики течения и визуализировать его. Были проведены эксперименты по внесению в струю возмущений посредствам колеблющейся с заданной частотой и фиксированной амплитудой проволоки. Визуализация течения показала, что при частотах, соответствующих теоретически полученному диапазону наиболее быстро растущих возмущений, струя разрушается ближе к выходу из формирующего устройства, чем при воздействии на струю возмущениями с частотами вне указанного диапазона. Были вычислены длины волн, возникающих в струе под воздействием возмущений, вызываемых колеблющейся проволокой. Эти длины волн хорошо коррелируют с длинами волн, полученными теоретически.
Исследование является первым шагом в экспериментальном изучении развития неустойчивости в затопленной струе круглого поперечного сечения и сравнении результатов с предсказаниями модальной теории устойчивости.
Работа поддержана РФФИ, проект №18-38-00745.
На рисунке - Схема устройства для внесения возмущений в струю и системы визуализации потока. Фотографии струи под воздействием возмущений с частотами 5 и 10 Гц.
[1] J. Zayko, S. Teplovodskii, A. Chicherina, V. Vedeneev, and A. Reshmin. Formation of free round jets with long laminar regions at large Reynolds numbers. 2018. Physics of Fluids, 30, 043603.
Олег Олегович Иванов
Пермский государственный национальный исследовательский университет
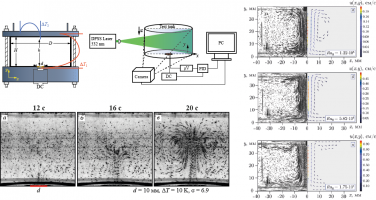
В ходе работы исследованы характеристики стационарного конвективного течения жидкости в цилиндрической полости, вызванного локализованным подогревом нижней границы. Опыты проводились с цилиндрическим слоем, у которого соотношение высоты к диаметру составляет H/D = 1 и 3 (рисунок). Высота рабочего слоя выбиралась равной 40 мм. Снизу полость ограничивалась массивом из оргстекла толщиной 25 мм, а сверху – алюминиевой пластиной толщиной 7 мм, либо оставалась открытой. С боковых сторон слой жидкости окружался трубкой из оргстекла с толщиной стенок 3 мм. Прозрачность боковой границы позволила исследовать структуру конвективных движений методом PIV. Для этого в рабочую полость, заполненную дистиллированной водой (0.97 г/см3), вносились светоотражающие частицы (1.05 г/см3), а при помощи вертикального лазерного ножа с длиной волны 532 нм вырезалась плоскость в центре слоя. Подогрев выполнялся за счет медного нагревателя диаметром d = 10 мм, расположенного в центре нижнего основания. С внутренней стороны медный теплообменник приводился в контакт с резистором. Для измерения температуры нагревателя ΔT1 внутри источника располагался спай дифференциальной термопары. Интенсивность подогрева поддерживалась постоянной за счет регуляции мощности тока, проходящего через резистор.
Имеющиеся результаты в виде термограмм ΔT2(t), зарегистрированных второй термопарой на высоте h = 37 мм над источником тепла, позволяют судить о длительности распространения теплового возмущения после включения источника тепла. Такой подход позволил исследовать зависимость времени достижения всплывающим конвективным факелом от степени подогрева. Однако существенное ограничение результатов этих исследований заключается в том, что, используя лишь сигнал термопары, нельзя получить представление о распространении факела раньше, чем он достигнет датчика температуры. Поэтому в ходе проведенного исследования уточнялась предлагаемая модель для скорости распространения конвективного факела [1]. Для этого применялась визуализация течения, которая позволила оценить продолжительность формирования конвективного течения и получить поправку для скорости распространения конвективной струи. Вместе с этим были исследованы характеристики установившегося течения при различных значениях управляющего параметра, в качестве которого использовалось число Рэлея Ra, а также для полостей с разным аспектным соотношением и граничными условиями на верхней стенке [2]. Кроме этого, на основе известной модели эволюции конвективного факела предприняты попытки обобщить теорию на случай течения в периодически изменяющемся инерционном поле.
Работа выполнена при поддержке РФФИ (проект 18-31-00165 мол_а).
1.Бабушкин И.А. и др. Развитие теплового плюма в узком вертикальном слое // Вестник ТГУ. Математика и механика. 2015. Т. 2, № 34. С. 41–52
2.Aminossadat S.M., Ghasemi B. A numerical study of mixed convection in a horizontal channel with a discrete heat source in an open cavity // European Journal of Mechanics - B/Fluids. 2009. Vol. 28, no. 4, P. 590–598
Иван Олегович Сбоев
НИИ механики МГУ
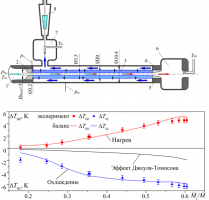
Экспериментально показано, что при истечении сжатого газа через трубку с проницаемыми стенками, возможно получить как минимум два потока с полными энтальпиями (полными температурами) отличными от начальной, т.е. осуществить безмашинное энергоразделение потока. В основе полученного результата лежит известный газодинамический эффект, возникающий при обтекании адиабатной поверхности сжимаемым газовым потоком с молекулярным критерием Прандтля отличным от единицы. Он заключается в перераспределении полной энтальпии в пограничном слое, вызванном дисбалансом между процессами выделения теплоты за счет работы сил вязкости и ее отвода в поток теплопроводностью. Если адиабатную поверхность сделать проницаемой, то возможно организовать вытекание слоев газа с полной энтальпией, отличной от начальной, за счет перепада давлений с внутренней и внешней стороны поверхности [1,2].
На рис.1 приведена схема экспериментального стенда и измеренные значения нагрева/охлаждения потоков в зависимости от массовой доли охлажденного потока. Зафиксировано, что при истечении сжатого воздуха через сверхзвуковое сопло, соединенное с трубкой с проницаемыми стенками, часть потока, просачивающегося сквозь стенки, имеет полную температуру ниже начальной, а оставшаяся часть – выше начальной. Эффект охлаждения почти в пять раз выше эффекта Джоуля – Томпсона для соответствующего перепада давлений и температуры
Андрей Геннадьевич Здитовец
Научно-исследовательский институт механики МГУ им. М.В. Ломоносова, Москва
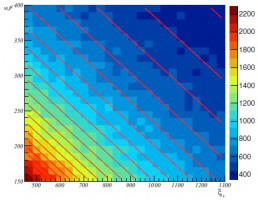
Проведены результаты экспериментальных исследований коэффициентов теплоотдачи и сопротивления на вихреобразующей поверхности в следе за поперечно установленным цилиндром. Коэффициент сопротивления определялся путем непосредственного взвешивания моделей на однокомпонентных тензометрических весах с учетом изменения статического давления на длине плавающих элементов. Для определения коэффициента теплоотдачи применялся метод нестационарного теплообмена с использованием ИК-камеры.
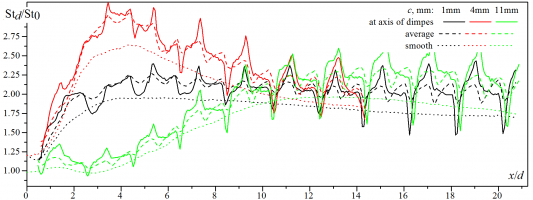
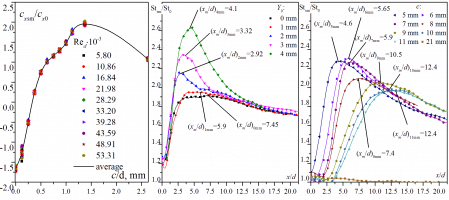
На расстоянии 796 мм от начала рабочего канала (длина 1080 мм, высота 30мм и ширина 300 мм) поперек потока (параллельно нижней стенке) устанавливался цилиндр диаметром d=8 мм. Зазор между нижней стенкой и цилиндром менялся в диапазоне 0-21 мм (цилиндр устанавливался с зазором в 0-11 мм с шагом 1 мм и с зазором 21 мм). Локальные значения коэффициентов теплоотдачи определялись на расстоянии x/d=0-20.625 от задней кромки цилиндра. Осредненные значения коэффициентов сопротивления определялись на участке x/d=12.5-20.625. В экспериментах исследовалась поверхность с шахматной компоновкой лунок с продольным и поперечным шагами 8 и 9 мм (глубина лунок – 1мм, диаметр пятна – 7.75 мм). Получены следующие результаты:
Значения относительного коэффициента сопротивления cxd/cxsm облуненной поверхности при зазоре c=21 мм незначительно превышает значение увеличения сопротивления в невозмущенном потоке. Далее величина cxd/cxsm растет при уменьшении зазора c. Это, по-видимому связано с тем, что величины коэффициентов сопротивления шахматных компоновок в невозмущенном потоке связаны с характерным взаимодействием лунок, расположенных в соседних рядах [1] – внесение крупномасштабных вихревых структур приводит к нарушению данного взаимодействия и увеличению коэффициента сопротивления.
Установка лунок приводит к увеличению неоднородности в поле коэффициентов теплоотдачи в следе за цилиндром в сравнении с гладкой стенкой. В первой части лунки (по направлению потока) наблюдается минимум коэффициентов теплоотдачи (по-видимому, вызванный наличием рециркуляционной зоны в этой области), у задней кромки наблюдаются максимальные значения коэффициентов теплоотдачи (область присоеднинения потока). При рассмотрении полей величин Std/St0 стоит отметить увеличение областей минимальных значений внутри лунок непосредственно за цилиндром (в области возвратных течений). Максимальные значения коэффициентов теплоотдачи при этом расположены при тех же значениях x/d, что и для гладкой стенке. Локальные значения интенсификации теплообмена на облуненной стенке варьировались в диапазоне Std/St0=0.9‑3.2 в зависимости от положения цилиндра.
Работа выполнена при поддержке грантов РФФИ № 18-08-00413 и СП-4006.2018.1.
1. van Nesselrooij M. et al. Drag reduction by means of dimpled surfaces in turbulent boundary layers // Exp. Fluids. Springer Berlin Heidelberg, 2016. Vol. 57, № 9. P. 1–14.
Николай Александрович Киселёв
Научно-исследовательский институт механики МГУ им. М.В. Ломоносова, Москва
Проведены результаты экспериментальных исследований коэффициентов теплоотдачи и сопротивления на гладкой поверхности в следе за поперечно установленным цилиндром. Коэффициент сопротивления определялся путем непосредственного взвешивания моделей на однокомпонентных тензометрических весах с учетом изменения статического давления на длине плавающих элементов. Для определения коэффициента теплоотдачи применялся метод нестационарного теплообмена с использованием ИК-камеры.
На расстоянии 796 мм от начала рабочего канала (длина 1080 мм, высота 30мм и ширина 300 мм) поперек потока (параллельно нижней стенке) устанавливался цилиндр диаметром d=8 мм. Зазор между нижней стенкой и цилиндром менялся в диапазоне 0-21 мм (цилиндр устанавливался с зазором в 0-11 мм с шагом 1 мм и с зазором 21 мм). Локальные значения коэффициентов теплоотдачи определялись на расстоянии x/d=0-20.625 от задней кромки цилиндра. Осредненные значения коэффициентов сопротивления определялись на участке x/d=12.5-20.625.
Получены следующие результаты:
Значения коэффициента сопротивления гладкой поверхности cxsm/cx0, отнесенные к коэффициенту сопротивления гладкой поверхности в невозмущенном потоке cx0 менялись в диапазоне cxsm/cx0=(‑1.65)‑(1.95) в зависимости от положения цилиндра и не зависели от числа Рейнольдса набегающего потока. Минимальные значения cxsm/cx0=-1.65±0.07 соответствуют c=0 мм (цилиндр расположен на стенке), максимальные значения cxsm/cx0= -1.96±0.06 соответствуют c=0 мм (цилиндр расположен на оси канала). При дальнейшем увеличении зазора c величина cxsm/cx0 начинает уменьшаться и достигает величины cxsm/cx0=1.08±0.03 при c=21 mm, т.е. при удалении цилиндра от стенки его влияние на динамический пограничный слой на стенке в канале практически не существенно.
Стоит отметить существенную неоднородность в распределении коэффициента теплоотдачи для всех положений цилиндра (кроме случая c=21 mm): сначала Stsm/St0 увеличивается от минимальных значений Stsm/St0=0.97-1.24 (наблюдаемых непосредственно у задней кромки цилиндра) до максимальных значений Stsm/St0=1.91-2.64 в зависимости от положения цилиндра. Положение максимума Stsm/St0 соответствует точке присоединения потока и, в диапазоне c=2-8 mm, находится в хорошем соответствии с зависимостью, предложенной в работе [1] для течения на пластине.
Работа выполнена при поддержке грантов РФФИ № 18-08-00413 и СП-4006.2018.1.
1. Suzuki K. et al. Study on a Turbulent boundary Layer Disturbed by a Cylinder-Effect of Cylinder Size and Position // Turbul. Shear Flows / ed. Durst F. et al. Berlin, Heidelberg: Springer Berlin Heidelberg, 1991. Vol. 7. P. 119–135.
Николай Александрович Киселёв
Финансовый университет при Правительстве РФ
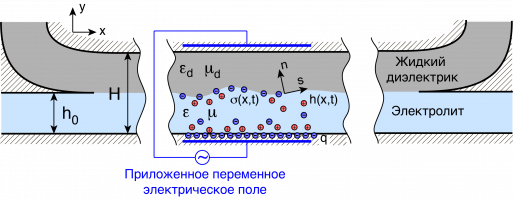
В данной работе рассматривается двухслойная система электролит-диэлектрик со свободной поверхностью раздела под действием внешнего электрического поля. Неустойчивость поверхности раздела является ключевым механизмом, ответственным за перемешивание. В микромасштабах отсутствует классическая гидродинамическая турбулентность, и для эффективного перемешивания в таких условиях необходимо искать другие эффекты, вызывающие неустойчивость одномерных течений и формирование микровихрей.
Для приведения жидкости в движение в микромасштабах обычно используют электрическое поле: оно действует на ионы солей, растворенных в жидкости, и приводит к электроосмотическому течению. Задача перемешивания жидкостей, в принципе, может быть решена аналогично: необходимо только подобрать условия, при которых электроосмотическое течение теряет устойчивость [1]. Существуют и другие способы создания неоднородности, в том числе за счет переменного электрического поля, направленного перпендикулярно каналу с жидкостями [2]. Переменное электрическое поле, особенно высокочастотное, является, к тому же, более предпочтительным по сравнению с постоянным, потому что при этом удается избежать нежелательных химических реакций, приводящих к деградации электродов и появлению пузырьков газа. Для случая, когда электрическое поле направлено вдоль границы раздела, было обнаружено два типа неустойчивости: длинноволновый и коротковолновый, связанные с поверхностными и объемными силами соответственно [3]. Если электрическое поле направлено по нормали к свободной поверхности раздела, то возникает неустойчивость, схожая с неустойчивостью Тонкса-Френкеля [4]. Для случая высокочастотных электрических полей получены асимптотические результаты.
Работа выполнена при финансовой поддержке Совета по грантам Президента Российской Федерации, грант для молодых кандидатов наук МК-5302.2018.1 и РФФИ грант 18-58-15004-НЦНИ_а.
Георгий Сергеевич Ганченко