Механико-математический факультет МГУ имени М.В. Ломоносова, НИИ механики МГУ имени М.В. Ломоносова
Ротор Савониуса – один из широко известных типов вертикально-осевых ветротурбин. Имеет узнаваемую S-образную форму. Его существенным недостатком является то, что он способен развить относительно малую скорость вращения. Вследствие этого генерируемая ротором мощность мала по сравнению с другими распространенными типами роторов, например роторами Дарье или пропеллерного типа. Однако создаваемый ротором Савониуса крутящий момент относительно велик. Этот факт делает ротор пригодным для использования в качестве силового привода. Системы такого типа описаны, например, в [1].
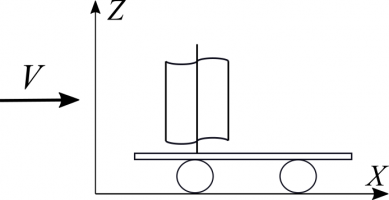
В настоящей работе рассматривается механическая система, состоящая из тележки, на которой установлен ротор Савониуса. Тележка может двигаться вдоль неподвижной оси ОХ и находится в потоке воздуха, движущемся с некоторой скоростью вдоль ОХ. Ось ротора соединена с колесами тележки и приводит их в движение. Предполагается, что колеса тележки могут катиться по плоскости с проскальзыванием. Аэродинамическая нагрузка, действующая на систему, вводится аналогично работе [2].
Получены условия существования и асимптотической устойчивости стационарного режима системы. Исследованы свойства движения тележки в зависимости от величины скорости ветра. Показано, что выбором соответствующих параметров системы, можно изменять направление движения тележки при фиксированной скорости ветра. Проведено численное моделирование системы.
Работа выполнена при поддержке грантов РФФИ (No. 17–08–01366, 18–01–00538).
1.Kassem, Y., Hüseyin, Ç. Wind Turbine Powered Car Uses 3 Single Big C-Section Blades.// Int. Conf. on Aeronautical & Manufacturing Engineering (ICAAME’2015), 2015, pages 42-45.
2. Klimina L.A., Masterova A.A., Selyutskii Yu. D., Hwang S.-S., Lin C.-H. On dynamics of a Savonius rotor-based wind power generator // Engineering Dynamics and Life Sciences (DSTA2017), 2017, pages 275-284.
Анна Андреевна Мастерова
Санкт-Петербургский политехнический университет Петра Великого
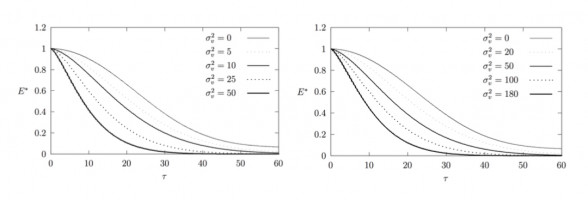
Рассматривается процесс перехода механической энергии в тепловую в нанокристалле без дефектов. Взаимодействие между частицами кристалла – нелинейное, учитывается влияние только ближайших соседей. Начальная температура кристалла задаётся случайными скоростями частиц с нулевым математическим ожиданием и равномерным распределением. Механическая энергия кристалла определяется энергией заданной на нём гармонической волны, после чего численно решается задача Коши для ячейки периодичности с последующим усреднением результатов по ансамблю реализаций [1].
Введение в модель идеального кристалла тепловых скоростей частиц приводит к необратимости распределения энергии волны между частицами, если тепловая энергия кристалла достаточно велика в сравнении с механической энергией [2]. В данной работе для реальных кристаллов показывается необратимость этого перехода, а также сохранение волной её первоначальной формы при уменьшающейся амплитуде. Убывание механической энергии со временем описывается модифицированным экспоненциальным законом, что позволяет определить коэффициент внутреннего трения кристалла и описать движение частиц с помощью уравнения продольных колебаний стрежня.
Результаты работы были получены с использованием вычислительных ресурсов суперкомпьютерного центра Санкт-Петербургского политехнического университета Петра Великого.
1. A. M. Krivtsov. Energy distribution in one-dimensional crystal. Dokl. Phys. 60 (9), page 407, 2015.
2. D. V. Tsvetkov, A. M. Krivtsov. Energy distribution in one-dimensional crystal. Proc. of XXIV ICTAM, pp. 2450-2451.
Егор Борисович Старобинский
НИИ механики МГУ
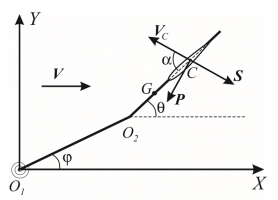
Рассматривается двухзвенный маятник, на втором звене которого закреплено тонкое крыло с симметричным аэродинамическим профилем, как показано в [1]. Вся система помещается в поток с постоянной скоростью V и монтируется таким образом, что обе оси маятника вертикальны. Первое звено маятника снабжено линейной спиральной пружиной. Введём систему отсчета, как показано на Рис.1. Ось абсцисс направлена по скорости потока. Выберем угол между этой осью и первым звеном и угол между этой осью и вторым звеном в качестве обобщенных координат. Предполагается, что пружина не напряжена, когда угол между первым звеном и осью абсцисс равен нулю, т. е. звено ориентировано «вдоль потока».
Чтобы описать аэродинамическую нагрузку на крыло, используется квазистатический подход, как например в [2]. В рамках этого подхода предполагается, что аэродинамическая нагрузка на крыло зависит только от мгновенного состояния движения системы. Получены условия асимптотической устойчивости положения равновесия «вдоль потока». Исследуется влияние положения крыла и жёсткости пружины на устойчивость. Увеличение расстояния, на котором крепится лопасть, ведёт к устойчивости системы, а увеличение жёсткости пружины на первом звене приводит к её потере.
Также, изучаются предельные циклы, возникающие в системе при определённых значениях параметров. Проанализирована зависимость их амплитуды и частоты от жёсткости пружин.
Эксперименты с таким маятником проводились в аэродинамической трубе Института механики МГУ. В ходе испытаний были определены характеристики колебательных режимов для разных скоростей ветра и различных положений крыла на втором звене. Показано, что экспериментальные данные качественно согласуются с результатами численного моделирования.
Работа выполнена при поддержке грантов РФФИ (No. 17–08–01366, 18–01–00538).
1. Голуб А.П., Селюцкий Ю.Д. О влиянии упругого крепления на колебания двух- звенного аэродинамического маятника // Труды Московского физико-технического института. 2017. No. 3. С. 8 – 13.
2. Klimina L., Dosaev M., Selyutskiy Yu. Asymptotic analysis of the mathematical model of a wind-powered vehicle // Applied Mathematical Modelling. Elsevier BV. 2017. Vol. 46. P. 691–697.
Андрей Петрович Голуб
ФИЦ ИПМ им.М.В.Келдыша РАН
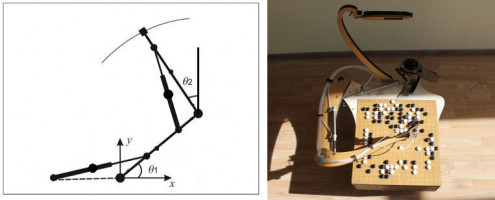
Основные типы приводов для современных робототехнических устройств технологически производятся с известными либо хорошо прогнозируемыми характеристиками. Знание этих характеристик позволяет разработчикам, пользуясь теорией автоматического регулирования, рассчитывать согласованные параметры управления и программы формирования движений. Однако такие методы плохо адаптируются для работы с пневматическими приводами, которые обладают значительными и плохо прогнозируемые упругостями, вызванными сжимаемостью воздуха в полостях пневмоцилиндров. Математическая модель, описывающая динамику пневматического привода, сложна для анализа. Эти обстоятельства затрудняют синтез управления традиционными средствами. Для построения системы управления манипулятора с пневматическими приводами используется нейронная система управления с обучением. В качестве простой экспериментальной модели с трудно формализуемыми свойствами, позволяющей в наглядной форме реализовать управление на основе нейронной сети, выбран двухзвенный манипулятор, кинематическая схема которого представлена на Рис. 1. Крепления звеньев и пневмоцилиндров представляют собой цилиндрические шарниры с одной степенью свободы. Положение системы определяется углами θ1 и θ2, представленными на схеме. В работе реализуется динамическая модель манипулятора с пневматическим приводом и строится система квазистатического позиционного управления, основанная на нейросетях.
Система управления представляет полносвязную нейронную сеть из 4-ех слоев. Входной слой нейросети получает начальные и целевые положения звеньев, в которые должна перейти система. На выходе нейронная сеть выдает вектор времен открытия клапанов пневматических цилиндров, которые переводят манипулятор из начального положения в целевое.
Для данной модели в среде Wolfram Mathematica построена и обучена нейронная система управления, которая позиционирует манипулятор с точностью менее 1 мм. Проведен сравнительный анализ с управлением, основанным на нейроподобном обучении, построенном в статье [2] для этого же манипулятора. В дальнейшем планируется реализовать данные алгоритмы на лабораторном прототипе робота и провести натурные испытание.
Данная работа выполнена при финансовой поддержке РФФИ, проект № 18-08-01441 А.
1. Neural network-based adaptive tracking control of mobile robots in the presence of wheel slip and external disturbance force, Ngoc-Bach Hoang, Hee-Jun Kang, Neurocomputing, 2016, 0925-2312
2. Квазистатическая модель манипулятора манго с нейроподобным управлением. В.Е.Павловский, А.В.Подопросветов, В.С.Смолин. Тр. XIX Международной научно-технической конференции ”Нейроинформатика-2017 Россия, Москва, 2-6 октября 2017. Ч.1, М.: НИЯУ МИФИ, (2017) с.50-59.
Алексей Валерьевич Подопросветов