Бигармонические аттракторы

Автор: Даниил Александрович Рязанов

Соавторы: Провидухина Мария

Организация: МГУ

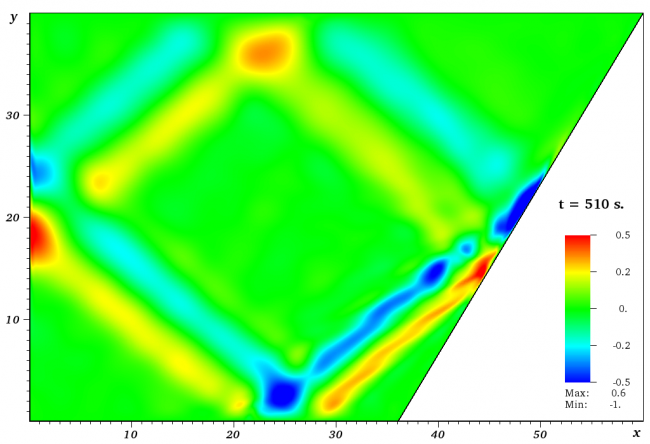
На рисунке: Вертикальная компонента скорости (слева) и динамика средней кинетической энергии (справа) при бигармоническом воздействии на стратифицированную жидкость.

В мировой океан со стороны солнца и луны постоянно поступает механическая энергия за счет приливного воздействия. Ранее были проведены исследования эффекта аккумуляции кинетической энергии стратифицированной жидкости, возникающих из-за особых свойств дисперсионного соотношения внутренних гравитационных волн при монохроматическом воздействии  [1]. Области аккумуляции кинетической энергии характеризуются повышенной скоростью движения жидкости и называются аттракторами. Аттракторы являются распространенным явлением в океане и любых стратифицированных жидкостях [2]. Это явление очевидно оказывает значительное влияние на перемешивание, траекторию движения живых организмов, седиментацию и эрозию поверхностей, с которыми они взаимодействуют. Следует отметить, что появление аттракторов присуще не только стратифицированным жидкостям, но и вращающимся. 

Моделирование аттракторов внутренних гравитационных волн на простой геометрии не требует больших вычислительных затрат и позволяет установить характерные режимы течения, оценить потенциал аккумулируемой энергии и проанализировать спектр компонент скорости [3].

В отличии от предыдущих работ, авторами численно получена картина течения стратифицированной жидкости в трапециевидном резервуаре с волнопродуктором воздействующим на жидкость двумя монохроматическими колебаниями (Рис. 1). Проведен анализ результатов прямого численного моделирования бигармонических аттракторов внутренних волн методом спектральных элементов. Исследован спектр вертикальной компоненты скорости, получена его частотно-временная характеристика и средняя кинетическая энергия в резервуаре в зависимости от времени.

1.      I. N. Sibgatullin, E. V. Ermanyuk, K. A. Vatutin, D. A. Ryazanov, and X. Xu. Numerical simulation of three-dimensional wave attractors. The XXVII workshop of the Council of nonlinear dynamics of the Russian Academy of Sciences, 47(1):112–115, 2019.

2.      Guo, Y., & Holmes-Cerfon, M. (2016). Internal wave attractors over random, small-amplitude topography. Journal of Fluid Mechanics, 787, 148-174. doi:10.1017/jfm.2015.648

3.      C. Brouzet, E. V. Ermanyuk, S. Joubaud, I. Sibgatullin, and T. Dauxois. Energy cascade in internal-wave attractors. Europhysics Letters, 113:44001, 2016.