ФГБОУ ВО "Пермский национальный исследовательский политехнический университет"
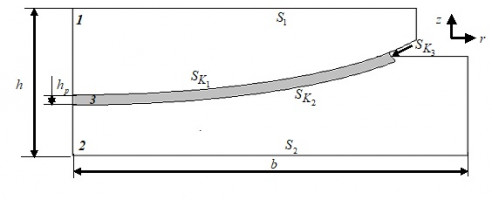
Ранее в [1] был отмечен ряд актуальных задач, связанных с геометрической конфигурацией опорных частей мостов. В работе рассмотрена задача анализа влияния толщины антифрикционного слоя на деформационное поведение конструкции сферической опорной части .
Характерные размеры сферической опорной части: максимальные высота 0,0483 м и ширина 0,155 м конструкции, толщина антифрикционной прослойки 3 0,004 м. В качестве материалов антифрикционной прослойки рассмотрено 6 материалов: три сверхвысокомолекулярных полиэтилена (СВМПЭ) разных производителей (мат. 1-3); два антифрикционных композиционных материала (мат. 4-5); модифицированный фторопласт (мат. 6).
В рамках серии численных экспериментов получены зависисмости распределения контактных параметров, интенсивности напряжения, интенсивности пластических деформаций и нормальных перемещений относительно свободного края слоя скольжения от толщины антифрикционной прослойки.
Установлено, что композиционные антифрикционные материалы больше подвержены деформированию. Данный эффект можно наблюдать на рис. 2: перемещения относительно свободного края прослойки из материалов 4-5 значительно больше и достигают 2,894 мм и 2,68 мм соответственно при толщине прослойки 4 мм, что в среднем в 5,6 раз больше, чем у других рассматриваемых материалов слоя скольжения.
Исследование выполнено за счет гранта Российского научного фонда (проект № 18-79-00147).
1. Adamov A.A., Kamenskikh A.A. The deformation behavior of modern antifriction polymer materials in the elements of transport and logistics systems with frictional contact // Advances in Intelligent Systems and Computing book series: Digital Science. – 2020. – Vol. 1114. – pp. 522-532.
Анна Александровна Каменских
МГУ
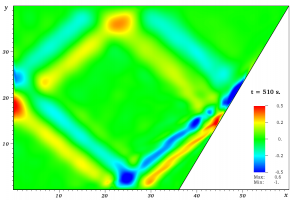
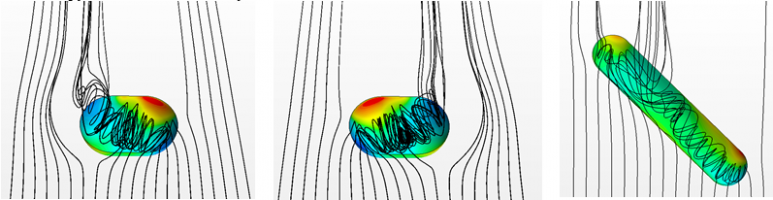
На рисунке: Вертикальная компонента скорости (слева) и динамика средней кинетической энергии (справа) при бигармоническом воздействии на стратифицированную жидкость.
В мировой океан со стороны солнца и луны постоянно поступает механическая энергия за счет приливного воздействия. Ранее были проведены исследования эффекта аккумуляции кинетической энергии стратифицированной жидкости, возникающих из-за особых свойств дисперсионного соотношения внутренних гравитационных волн при монохроматическом воздействии [1]. Области аккумуляции кинетической энергии характеризуются повышенной скоростью движения жидкости и называются аттракторами. Аттракторы являются распространенным явлением в океане и любых стратифицированных жидкостях [2]. Это явление очевидно оказывает значительное влияние на перемешивание, траекторию движения живых организмов, седиментацию и эрозию поверхностей, с которыми они взаимодействуют. Следует отметить, что появление аттракторов присуще не только стратифицированным жидкостям, но и вращающимся.
Моделирование аттракторов внутренних гравитационных волн на простой геометрии не требует больших вычислительных затрат и позволяет установить характерные режимы течения, оценить потенциал аккумулируемой энергии и проанализировать спектр компонент скорости [3].
В отличии от предыдущих работ, авторами численно получена картина течения стратифицированной жидкости в трапециевидном резервуаре с волнопродуктором воздействующим на жидкость двумя монохроматическими колебаниями (Рис. 1). Проведен анализ результатов прямого численного моделирования бигармонических аттракторов внутренних волн методом спектральных элементов. Исследован спектр вертикальной компоненты скорости, получена его частотно-временная характеристика и средняя кинетическая энергия в резервуаре в зависимости от времени.
1. I. N. Sibgatullin, E. V. Ermanyuk, K. A. Vatutin, D. A. Ryazanov, and X. Xu. Numerical simulation of three-dimensional wave attractors. The XXVII workshop of the Council of nonlinear dynamics of the Russian Academy of Sciences, 47(1):112–115, 2019.
2. Guo, Y., & Holmes-Cerfon, M. (2016). Internal wave attractors over random, small-amplitude topography. Journal of Fluid Mechanics, 787, 148-174. doi:10.1017/jfm.2015.648
3. C. Brouzet, E. V. Ermanyuk, S. Joubaud, I. Sibgatullin, and T. Dauxois. Energy cascade in internal-wave attractors. Europhysics Letters, 113:44001, 2016.
Даниил Александрович Рязанов
ИПМ им. М.В. Келдыша РАН.
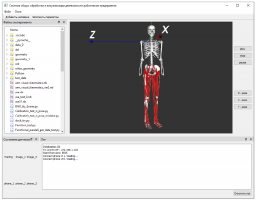
Данное исследование посвящено внедрению экзоскелетов в промышленность. Целью является создание комплекса программных и аппаратных средств для распознавания движений человека, необходимого для проведения экспериментов, направленных на достижения двух основных задач. Во-первых, показать энергоэффективность экзоскелетов для людей, которые используют экзоскелеты в обычных производственных задачах. Во-вторых, создать уникальную интеллектуальную систему управления для автоматической помощи оператору полупассивного экзоскелета, и предоставить рекомендации по ведению рабочих процессов. Проделанная работа заключается в разработке программного комплекса, с алгоритмами сбора и хранения данных, реконструкции траектории движения человека, системы визуализации данных и оптимизации модели человека. Полученная система позволяет быстро и точно собирать данные в производственных условиях для подсчета энергоэффективности экзоскелетов. Данный программный комплекс позволит собрать достаточно данных для применения методов машинного обучения в системе управления экзоскелетом.
Рассматривается упрощённая модель тела человека, состоящая из десяти звеньев, по два на каждую конечность и два звена на спину. Каждое звено неотрывно прикреплено к предыдущему сферическим шарниром. Ориентация каждого звена определяется по показаниям IMU-датчиков соответственно надетых на человека. Предполагается, что на человеке надето столько же датчиков, сколько и звеньев в модели, при том в соответствующих местах. На начальном этапе известна примерная точка крепления датчика на теле, а ориентация датчика может быть произвольной. Для ее вычисления проводится двух этапная калибровка. В рамках разработки системы визуализации решаются задачи оптимизации длин звеньев модели человека и задача восстановления траекторий движения частей тела. Затем производится экспериментальная проверка качества откалиброванной модели. По восстановленным траекториям эксперимента решается прямая задача динамики, и оценивается энергия, затрачиваемая человеком при совершении действий в эксперименте.
1. Подопросветов А.В., Анохин Д.А., Орлов И.А., Алисейчик А.П. Разработка системы управления биомеханическим комплексом помощи работникам производственных предприятий // В сборнике: XII Всероссийский съезд по фундаментальным проблемам теоретической и прикладной механики сборник трудов в 4-х томах. 2019. С. 196-198.
Алексей Валерьевич Подопросветов
НИИ механики МГУ имени М.В. Ломоносова
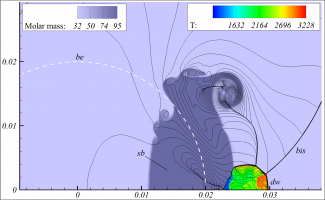
На основе уравнений Эйлера для совершенного газа с неоднородной молярной массой моделируется взаимодействие ударной волны в горючем газе с эллипсоидальным пузырем инертного газа повышенной плотности в двумерной постановке. Рассмотрены различные числа Маха M падающей волны и отношения длин полуосей пузыря. Для численного моделирования применяется конечно-объемный метод типа С.К. Годунова второго порядка аппроксимации, включающий HLLC-решатель локальных задач о распаде разрыва. Реакция горения газовой смеси моделируется с помощью двухстадийной кинетики Коробейникова-Левина.
Описаны различные режимы воспламенения смеси и показана их существенная зависимость как от интенсивности падающей волны, так и от формы пузыря. При достаточно больших числах Маха падающей волны инициирование горения смеси происходит непосредственно за счет разогрева в ударной волне. Для более слабых скачков воспламенение может происходить при отражении падающей ударной волны от границы раздела газов (рис. 1, слева), а для еще более слабых – в области фокусировки поперечных скачков вблизи подветренного полюса пузыря (рис. 1, справа).
Показано, что форма пузыря играет также важную роль, во многих случаях обеспечивая инициирование горения пузыря более слабой волной, или наоборот, отсутствие воспламенения по сравнению со сферическими пузырями.
Работа выполнена в НИИ механики МГУ имени М.В. Ломоносова с использованием ресурсов суперкомпьютерного комплекса МГУ имени М.В. Ломоносова при частичной финансовой поддержке Совета по грантам президента РФ (МК-3012.2019.1) и Российского фонда фундаментальных исследований (18-01-00793).
Олег Георгиевич Сутырин
НИИ механики МГУ им. М.В. Ломоносова
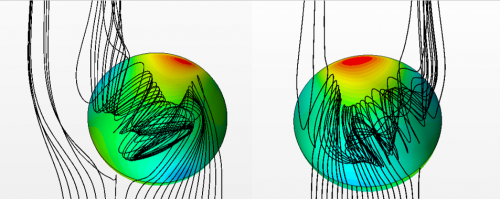
Изучение луночных углублений и их характеристик уже длительное время остается актуальной задачей современной механики и теплофизики. Подобные углубления являются хорошими интесификаторами теплообмена, не вызывающими, при этом существенного роста гидравлического сопротивления [1]. На практике этой свойство применяется при разработке теплообменных устройств макро- и микро-масштабов. Структура обтекания подобных углублений существенно зависит от относительной глубина (H/D). Так называемые «мелкие» лунки (H/D<0.25), характеризуются стационарным режимом обтекания, при котором в большинстве случаев, наблюдаются два симметричных вихря. При повышении отношения H/D до 0.25 стационарная структура потока в окрестности лунки разрушается и наблюдается формирование несимметричного течения с непериодическим чередованием «левостороннего» и «правостороннего» режима.
В настоящем исследовании проводится численное моделирование обтекания глубокой лунки (H/D=0.5) турбулентным потоком вязкой несжимаемой жидкости. Лунка располагается на нижней стенке плоскопараллельного канала, высотой 0.83 D. Входная и выходная границы канала расположены на расстоянии 4.5D, а расстояние от кромки лунки до боковых стенок канала составляет 1.5. Для описания турбулентного течения используется метод моделирования крупных вихрей (LES) c подсеточной моделью WALE [2]. Расчеты проведены для двух чисел Рейнольдса, вычисленных по диаметру лунки, ReD = 10 000 и ReD = 40 000. Для генерации турбулентности на входе использовался метод SEM (Synthetic Eddy Methods) [3].
Проведенные расчеты показали, что на наличие переключающихся режимов, кроме глубины лунки оказывает влияние и число Рейнольдса. Получено, что при ReD = 10 000 внутри лунки формируется практически симметричная вихревая структура, несимметричные переключающиеся структуры отсутствуют. Существенно иная картина формируется при увеличении числа Рейнольдса до 40 000. Наблюдается наличие переключающихся режимов, которые представляют собой одноядерные наклонные вихревые структуры, которые начинаются в одном конце лунки, пересекают продольную плоскость симметрии и выходят с противоположенного конца. Осреднение по трем циклам дает в среднем близкую к симметричной картину, которая при этом отличается от полученной для ReD = 10 000. Кроме того, было проведено осреднение за период существования одного режима, в этом случае получается характерная одноядерная вихревая структура.
Работа выполнена при финансовой поддержке РФФИ (грант № 19-01-00242).
1.Дзюбенко Б.В., Кузма-Кичта Ю.А., Леонтьев А.И., Федик И.И., Холпанов Л.П. Интенсификация тепло- и массообмена на макро-, микро- и наномасштабах. - М.: ФГУП “ЦНИИАТОМИНФОРМ”, 2008, с цв.вкладкой
2.Nicoud, F. and Ducros, F., 1999. “Subgrid-Scale Stress Modelling Based on the Square of the Velocity Gradient Tensor,” Flow, Turbulence and Combustion, 62, pp. 183-200.
3.Jarrin, N., Benamadouche, S., Laurence, D., and Prosser, R. 2006. “A synthetic-eddy-method for generating inflow conditions for large eddy simulations”. International Journal of Heat and Fluid Flow, 27, pp. 585-593
Алексей Юрьевич Чулюнин
НИИ механики МГУ им. М.В. Ломоносова
Исследование механизмов обтекания лунок различной глубины, является актуальной задачей современной механики. Известно, что подобные углубления являются хорошими интенсификаторами теплообмена и не вызывают при этом сильного роста коэффициента гидравлического сопротивления. В зависимости от отношения максимальной глубины H и диаметра пятна D принято различать мелкие (H/D<0.125), умеренные (0.125 <Δ< 0.25) и глубокие (H/D>0.25) лунки [1]. В мелких лунках течение безотрывное, а в умеренных – возникают характерные вихревые структуры в виде симметричной двухъячеистой области рециркуляционного течения. В глубоких лунках стационарные схемы течения оказываются неустойчивыми, наблюдается формирование нестационарного течения с непериодическим чередованием «левостороннего» и «правостороннего» несимметричных режимов. Последние работы (например, [2]) показывают, что эффективная форма вихрегенератора – овально-траншейная лунка (ОТЛ).
В работе на базе численного моделирования исследуется структура течения в глубоких овально-траншейных лунках, расположенных различными углами к набегающему потоку, на нижней стенке плоскопараллельного канала. Траншея представляет собой две половинки полусферической лунки радиуса R, соединенных между собой полуцилиндрической вставкой, длина которой L варьируется в широком диапазоне. Для дискретизации расчетной области применялась неструктурированная сетка размером до 15 млн. элементов. Число Рейнольдса вычисленное по скорости потока на входе в канал и диаметру начального пятна лунки изменяется в диапазоне от 104 до 105.
В ходе проведения вычислительного эксперимента выявлено, что увеличение длины цилиндрической части лунки от 0 до L=R приводит к стабилизации течения, воспроизводятся два устойчивых стационарных состояния, характеризуемые одноядерными вихревыми структурами, начинающимися на внутренних стенках концевых сферических скруглений траншеи и выходящих во внешнюю пристеночную область течения в районе противоположных концов траншеи (Рис.1а, б). Конкретная конфигурация зависит от предыстории установления, в частности – от начальных условий задачи. Дальнейшее увеличение длины лунки, а также поворот лунки относительно набегающего потока устраняет неоднозначность решения и приводит к новым, более сложным вихревым структурам (Рис.1в).
Алексей Юрьевич Чулюнин
НИИ механики МГУ им. М.В. Ломоносова
Исследуется эффективность газового воздействия на нефтяной пласт, в рамках моделирования смешивающегося вытеснения в пористой среде при закачке углеводородного (УВ) газа. Для описания течения в пористой среде, используется композиционная модель фильтрации, позволяющая учесть изменения компонентного состава жидкостей и газов в пласте, теплофизические свойства которых задаются уравнением состояния Ван-дер-Ваальсового типа. Эффективность нефтеотдачи сравнивается с получаемой при применении традиционной технологии заводнения. Для проведения исследований разрабатывающийся авторами комплекс программ MUFITS [1,2] дополнен модулем для композиционного моделирования фильтрации. На данном примере демонстрируются его обновленные функциональные возможности.
В модели учитывается, что в зависимости от давления и температуры УВ смесь находится либо в однофазном состоянии газа или жидкости (нефти), либо в двухфазном состоянии газ–нефть. Вода же не смешивается с УВ, образуя отдельную компоненту жидкости. Давление во всех фазах считается одинаковым – капиллярное давление пренебрежимо мало, изменение температуры – тоже. Течение происходит в тонком горизонтальном пласте, влиянием силы тяжести пренебрегается.
Рассматриваются модельные составы нефти и вытесняющего газа, совпадающие с одними из предложенных в [3] – случай A. По постановке задача является автомодельной задачей Римана. Её решение состоит из последовательности сильных разрывов (S), на которых рвутся распределения насыщенностей газа sg и воды sw, полные концентрации компонент смеси zi; центрированных волн Римана (R) и областей однородного распределения параметров, распространяющихся от входной границы внутрь области (S4-S3RS2-S1). В случае B в пласт закачивается вода, а решение содержит только один разрыв и одну волну Римана (R*S*) – случай B. Результаты численного моделирования приведены на рис. (рис. Распределения насыщенностей газа и воды в случаях А и B (а) и полных мольных концентраций в задаче А (б), соответственно.)
Исследованы характерные времена, на которых закачка газа позволяет извлечь наиболее ценные УВ компоненты нефти. Показано, что закачка воды в целом более эффективный метод повышения нефтеотдачи из пластов, насыщенных нефтью рассмотренного модельного состава. Газовое воздействие позволяет извлечь дополнительное количество промежуточных компонент УВ ряда только после закачки 3 поровых объемов газа. Однако, это дополнительное количество мало и, по-видимому, не имеет практической значимости. Еще меньший эффект достигается при вытеснении тяжелых компонент.
1. Afanasyev A.A. Hydrodynamic modelling of petroleum reservoirs using simulator MUFITS// Energy Procedia. 2015. V. 76. P. 427–435.
2. Afanasyev A., Kempka T., Kühn M., Melnik O. Validation of the MUFITS reservoir simulator against standard CO2 storage benchmarks and history-matched models of the Ketzin pilot site // Energy Procedia. 2016. V. 97. P. 395–402.
3. Orr F.M. Theory of gas injection processes. Holte, Denmark: Tie-Line Publications, 2007. 381 p.
Елена Анатольевна Веденеева
ИПМ им. М.В. Келдыша РАН.
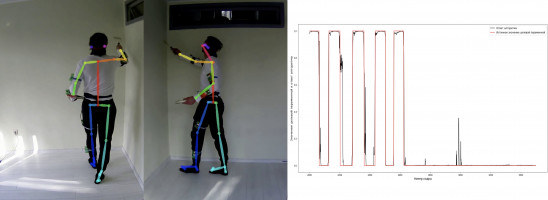
В последнее время возрастает необходимость в улучшении условий работы сотрудников предприятий для повышения эффективности и снижения травмоопасности рабочих процессов. Использование промышленных экзоскелетов стало одной из основных концепций, направленных на решение данной задачи. Наибольшее распространение получили пассивные экзоскелеты, однако они не всегда могут необходимым образом и в нужный момент перераспределить нагрузку. Больший интерес вызывают полуактивные конструкции. Для определения моментов времени включения и выключения экзоскелетов требуется определять как основные действия оператора (ОД – ходьба, поднятие рук, и т.п.), так и переходные действия (ПД – процесс подъёма тяжести).
Целью работы является создание модели классификации действий человека с наилучшей метрикой качества, используя видеопоследовательности. В работе рассматривается задача классификации целевых действий человека по данным, получаемым с оптических датчиков (ранее было рассмотрено решение, основанное на инерциальных датчиках [2]). В качестве примера рассматривается задача покраски стены с двумя целевыми бинарными переменными: угол между плечом и туловищем больше или меньше критического, и целевое состояния – красит человек стену или нет.
В рамках задачи были сняты 5 пар параллельных видео с двух разных ракурсов длительностью по 6 минут каждое, на которых человек занимается покраской стены. Для получения информации с кадра была выбрана система OpenPose [1], которая для каждого кадра видео возвращала координаты ключевых точек человека, изображенного на кадре. Таким образом, была собрана обучающая выборка с номером кадра, двумя бинарными целевыми переменными и координатами 25 ключевых точек на человеке.
По результатам анализа построенных моделей был выбран алгоритм XGBClassifier. Для сравнения моделей были выбраны метрики ROC AUC и Accuracy. Полученные результаты обучения на первом целевом действии дают точность ROC AUC – 98% и Accuracy – 94%, на втором целевом действии – ROC AUC – 99% и Accuracy – 95%.
1. Cao Z. et al. OpenPose: realtime multi-person 2D pose estimation using Part Affinity Fields //arXiv preprint arXiv:1812.08008. – 2018.
2. Подопросветов А.В. и др. Разработка системы управления биомеханическим комплексом помощи работникам производственных предприятий // В сборнике: XII Всероссийский съезд по фундаментальным проблемам теоретической и прикладной механики сборник трудов в 4-х томах. 2019. С. 196-198.
Алексей Валерьевич Подопросветов
АО "ОКБМ Африкантов"
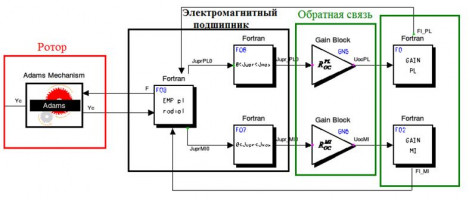
Одной из задач проектирования роторной системы на электромагнитном подвесе является определение и минимизация нагрузок, приходящих на опоры, определение прогибов и напряженного состояния её элементов. Особенности конструкции роторной системы приводят к необходимости разработки алгоритма связного решения задач управления движением и динамики ротора (см. рисунок). Приемлемых результатов моделирования в данном случае можно достичь с использованием комплекса современных программных средств и экспериментальных данных.
В докладе представлено использование технологии компьютерного моделирования вращения гибкого ротора с учетом системы управления электромагнитными подшипниками. При компьютерном моделировании роторной системы учтены особенности взаимодействия гибкого ротора с электромагнитными подшипниками и нагрузки, влияющие на его динамику. Рассмотрено возможное взаимодействие ротора со страховочными подшипниками в случае сейсмического воздействия. При этом определены параметры и особенности взаимодействия ротора со страховочными подшипниками.
1. Белов С.Е., Кодочигов Н.Г., Патрушев В.Л., Руин А.А., Соловьев С.А. Аналитические исследования динамики вращения ротора при отказе резервных подшипников // Вестник Нижегородского университета им. Н.И. Лобачевского.–2011.–№4.–С.63-64.
2. S. Malkin, D. Balandin. On stability of the electromagnetic suspension rotor in space of control parameters // Cybernetics and Physics. –2017.–Vol. 6, NO. 4.–P.147-151.
Константин Александрович Лонин
ЦАГИ, МГУ
На рисунке: Вверху – одна из первых исследуемых в работе компоновок разрабатываемого сверхлегкого самолета; в центре – зависимость подъемной силы от скорости взлета/посадки, внизу – зависимость подъемной силы от скорости полета.
Создание сверхлегких пилотируемых летательных аппаратов представляет практический интерес с точки зрения быстрой, безопасной и экономичной транспортировки грузов и человека.
Разрабатываемый сверхлегкий бесфюзеляжный самолет содержит несущую поверхность, стабилизатор, подвесную систему, систему управления и воздушный винт, отличается тем, что дополнительно содержит балку, крепящуюся к крылу и стабилизатору, четное количество расположенных на несущей поверхности электродвигателей с воздушными винтами, стропы, которые связывают несущую поверхность и балку с подвесной системой, на которой также расположен источник энергии, модуль дистанционного управления и электрическая трансмиссия, связывающая источник энергии с электродвигателями.
Уменьшение размеров летательных аппаратов ограничена размерами и весом летчика и превращает самолет по сути в некое подобие летательного костюма (рис. 1 вверху). Подготовлен обзор известных аналогов, показаны преимущества и области применения разрабатываемого летательного аппарата: например, экономичный и доступный личный транспорт, военные приложения, эвакуация, поисково-спасательные работы, перевозка грузов и оборудования широкого спектра назначения. Проектируемый самолет не требует аэродрома, обладает малым весом (40–45 кг), возможностью разборки для перевозки в личном и в общественном транспорте. Винтовая схема обеспечивает экономичность, дальность и продолжительность полета, при этом шум значительно ниже в отличие от реактивных аналогов. Оригинальная аэродинамическая компоновка обеспечивает низкие затраты электроэнергии двигателей при полном отсутствии вредных выбросов в атмосферу. Модификация аппарата для военных приложений обеспечивает высокую скорость, точность и низкую заметность. Статическая устойчивость в горизонтальном полете дает возможность пилоту освободить руки и использовать их для управления другими действиями. На рис. 1 внизу и в центре представлены результаты расчета зависимости подъемной силы летательного аппарата с крыльями различных конфигураций от скорости полета. Видно, что геометрия 10 обеспечивает достаточную подъемную силу при влете и посадке со скоростью 30–35 км/ч, которую можно снизить за счет применения разработанное ранее адаптивное крыло.
Иван Алексеевич Амелюшкин
Центральный аэрогидродинамический институт им. проф. Н.Е. Жуковского, Московский государственый университет имени М.В. Ломоносова

Использование гидрофобных покрытий представляет интерес в широкой области технических и бытовых приложений, в частности в задачах противодействия обледенению летательных аппаратов. Гидрофобные поверхности обладают своеобразными функциональными свойствами, к которым следует отнести водонепроницаемость, стойкость к коррозии, устойчивость к биообрастанию, к неорганическим, а в ряде случаев и к органическим загрязнениям. Благодаря многообразию управляемых свойств создание гидрофобных тел в настоящее время интенсивно развивается. Такие покрытия, как правило, эффективно работают при незначительных числах Вебера, рассчитанных по характерным размерам H рельефа поверхности We = HρV2/σ, (ρ – плотность жидкости, σ – коэффициент поверхностного натяжения, V – скорость удара капли). Однако при превышении поверхностной плотности кинетической энергии (переохлаждённой капли) некого критического значения, льдофобные свойства приводят к отрицательным эффектам ввиду проникновения жидкости в углубления и застывания в них. В случае динамического воздействия свойства гидрофобных/льдофобных покрытий определяются коэффициентами отскока капель в зависимости от числа Вебера. Достоверность полученных результатов обоснована сравнением с теоретическими и экспериментальными оценками других исследователей. Проведены параметрические исследования прилипания жидкости к рельефным покрытиям твердого тела, которые сформированы из комбинации гидрофобных и льдофобных материалов.
Иван Алексеевич Амелюшкин
ФГБУН Институт прикладной механики РАН
Пляска проводов воздушных линий электропередачи представляет собой самовозбуждающийся колебательный процесс с аэродинамической обратной связью, обусловленной изменением действующей на провод с гололедом подъемной силы при изменении угла атаки. Пляска относится к низкочастотным видам колебаний (0.15–1.0 Гц) и характеризуется значительными амплитудами [1, 2]. Наиболее опасной, как правило, является однополуволновая пляска, при которой амплитуды вертикальных колебаний проводов и соответствующие вариации силы натяжения максимальны [3].
Многочисленные наблюдения и экспериментальные исследования показывают, что при пляске, наряду с выраженными вертикальными движениями проводов, имеют место синхронизированные с ними крутильные колебания. Закручивание сечения провода приводит к дополнительному увеличению подъемных сил и, как следствие, амплитуд пляски по сравнению с «чистым» вертикальным движением проводов по Ден-Гартогу [1].
В модели провод разбивается на конечные элементы, его относительное удлинение записывается с учетом влияния температурного расширения и технологического запаса по длине. Угол кручения сечения и осевые перемещения записываются в пределах элемента по методу Ритца. Считаем, что системы координат сечения льда и провода связаны жестким образом, их начала лежат в центре жесткости системы. Динамика процесса описывается с помощью принципа Д’Аламбера-Лагранжа: вычисляются вариации потенциальной энергии системы, работы инерционных и внешних сил, определяются коэффициенты при вариациях обобщенных координат.
Получившаяся система нелинейных дифференциальных уравнений приводится к форме Коши и интегрируется численно. Начальные условия для интегрирования находятся из решения задачи статики, уравнения которой получаются путем исключения инерционных членов из динамической задачи. Решать задачу статики можно с помощью метода продолжения по параметру.
1. CIGRÉ Technical Brochure 322, "State of the art of conductor galloping", by Task Force B2.11.16, Sept 2003.
2. Виноградов А.А., Данилин А.Н., Рабинский Л.Н. Деформирование многослойных проволочных конструкций спирального типа. Математическое моделирование, примеры использования. – М.: Изд-во МАИ, 2014. – 168 с.
3. Havard D.G. Detuning for controlling galloping of single conductor transmission lines // IEEE Symposium on Mechanical Oscillations of Overhead Transmission Lines. Paper A 79 500-0. – Vancouver, Canada. July 1979.
Руслан Анатольевич Шавня
Научно-исследовательский московский комплекс «Центральный аэрогидродинамический институт им. проф. Н.Е. Жуковского»
Существует широкий класс задач, в которых происходит аэродинамическое взаимодействие движущихся в воздушной или иной сплошной средой тел с близко расположенной неподвижной поверхностью (экраном). Практическими примерами, где реализуются такие течения, являются: летательные аппараты на режиме взлёта/посадки, движение экраноплана в штатном режиме, течения в зазорах между автомобильным транспортом и дорожным полотном, между составом метро или, скажем, аппарата Hyperloop компании Tesla и тоннелем.
В случае экранного эффекта для несущих поверхностей условно можно выделить два случая: область «нормального» экранного эффекта, когда при приближении к экрану с бесконечности до некоторого расстояния подъёмная сила увеличивается, и «аномального», когда, начиная с некоторого расстояния от экрана при дальнейшем приближении, подъёмная сила начинает уменьшаться. Подавляющая часть работ посвящена исследованию в области «нормального» экранного эффекта (например, [1]). При этом при существующей в различных работах параметрике отсутствует разделение на отдельное влияние несущих свойств и толщины (телесности, объёма) исследуемого тела на исследуемый эффект.
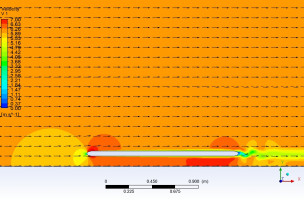
В работе представлена попытка рассмотреть задачу влияния телесности объекта на экранный эффект, для чего проведены серии двумерных аэродинамических расчётов вязкого обтекания плоской телесной пластины над неподвижной безграничной поверхностью. На рисунке приведён пример такого течения. В качестве валидации расчётной методики приведено сравнение с экспериментальными результатами полей скоростей в зазоре между движущейся пластиной и неподвижной поверхностью [1].
Параметрами задачи являлись: толщина пластины, расстояние между пластиной и экраном, число Рейнольдса. Из анализа графиков интегральных аэродинамических сил можно заключить, что даже для не обладающего в безграничном потоке несущими свойствами тела (плоская телесная пластина), экранный эффект сопровождается явлением возникновения подъемной силы. Подробный анализ структуры течения в зазоре между движущейся пластиной и неподвижной поверхностью позволяет выявить причину такого неожиданного поведения, которое в своей основе связано с особенностями обтекания передней и задней кромок пластины.
1. Айрапетов А.Б., Катунин А.В. Анализ средствами математического моделирования особенности аэродинамики моделей ЛА при испытании в АДТ на стендах с различными схемами, моделирующими приэкранную аэродинамику// Сборник докладов XI международной научной конференции по амфибийной и безаэродромной авиации «Гидроавиасалон-2016». М., 2016 г. С. 130.
Андрей Владимирович Катунин
НИИ Механики МГУ, Москва
На активных вулканах часто наблюдаются перемещения поверхности Земли, величина которых может достигать нескольких метров. Периоды подъема и опускания поверхности хорошо коррелируют с периодами повышенной и пониженной вулканической активности [1]. В таких вулканических системах магматический очаг залегает на глубине нескольких километров под поверхностью Земли. При остывании из очага отделяются летучие компоненты, в основном водяной пар и углекислый газ, которые по проницаемым вмещающим породам поднимаются к поверхности. При этом давление и температура жидкости являются источниками напряжений, деформирующих вмещающие породы.
Традиционный полуаналитический подход к моделированию деформаций пород, рассматриваемый в литературе, заключается в том, что каждая ячейка расчетной сетки считается независимым источником деформаций. Для этой ячейки из аналитического решения о нагружении полубесконечной плоскости точечным источником рассчитывается поле перемещений, а полный вектор перемещений в какой-либо точке пространства получается путем суммирования вкладов всех ячеек. Такой подход работает только в предположении плоской поверхности Земли и однородного распределения механических свойств среды по пространству.
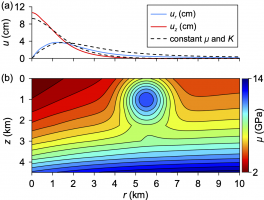
Целью настоящей работы является создание метода, позволяющего рассчитывать деформации пород с учетом механических неоднородностей. Для тестирования этого метода проводится численное моделирование напряженно-деформированного состояния пород в процессе дегазации магматического очага в гидротермальной системе Campi Flegrei. Жидкая и газовая фазы моделируются двухкомпонентной смесью вода-углекислый газ, а твердая фаза, т.е. проницаемые породы, моделируется линейной термопороупругой средой. Расчет фильтрации жидкости и газа производится в симуляторе MUFITS, а расчет напряжений и перемещений пород производится методом конечных разностей в отдельной программе. Обратное влияние деформации пород на механику жидкости не учитывается.
Проведено сравнение нового метода с полуаналитическим подходом, исследовано влияние граничных условий на результаты расчетов. Проведены расчеты деформаций пород для случая неоднородного распределения модуля сдвига и коэффициента Пуассона по пространству. Показано, что в диапазоне значений механических свойств пород, характерных для системы Campi Flegrei, учет наличия неоднородности несущественно влияет на значения перемещений поверхности.
Работа выполнена в рамках проекта РНФ №19-71-10051.
1.Rinaldi A. P., Todesco M., Bonafede M. Hydrothermal instability and ground displacement at the Campi Flegrei caldera // Physics of the Earth and Planetary Interiors. Год 2010. Т. 178. №. 3-4. С. 155-161.
Иван Сергеевич Уткин
ФГБОУ ВО "Пермский национальный исследовательский политехнический университет"
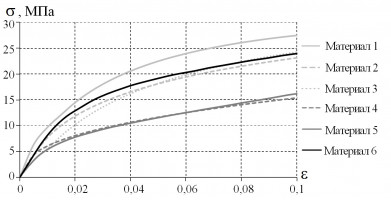
Существует большой набор полимерных материалов и композитов на их основе российского и зарубежного производства, пригодных к использованию в качестве антифрикционных покрытий и прослоек в узлах конструкций, работающих в рамках контактного взаимодействия с трением [1]. Экспериментальное исследование свойств таких материалов и построение численных моделей их поведения в рамках механики контактного взаимодействия являются актуальными направлениями исследования.
В рамках работы выполнено междисциплинарное исследование деформационного поведения ряда современных антифрикционных полимерных материалов и композитов на их основе:
1. Серия натурных экспериментов по определению физико-механических, фрикционных и реологических свойств материалов с идентификацией модели их поведения.
2. Анализ влияния свойств современных антифрикционных полимерных материалов в рамках численных моделей экспериментов на стесненное и свободное сжатие цилиндрических образцов диаметром и высотой 20 мм плитами пресса.
3. Численное моделирование деформационного поведения исследуемых материалов в реальных конструкциях.
При численном моделировании напряженно-деформированного состояния тестовых задач и реальных конструкций было исследовано 6 полимеров и композитов на их основе (материалы 1-6). В качестве первого приближения, для описания модели поведения материалов выбрана деформационная теория упругопластичности (рис. 1).
Установлено, что наилучшими деформационными характеристиками обладает СВМПЭ наполненный углеродом (материал 1), но для построения и идентификации качественной модели его поведения нужны дополнительные экспериментальные исследования с различными историями длительного многоступенчатого нагружения; композиционные материалы на основе фторопласта 4 (материалы 4-5) обладают при стесненном и свободном сжатии более значимыми нелинейными и вязкоупругими эффектами, а также большей податливостью по сравнению с другими исследуемыми материалами, при дендритной форме частиц более заметны реологические эффекты.
Исследование выполнено за счет гранта РФФИ (№18-08-00903).
1. Адамов А.А., Каменских А.А., Носов Ю.О. Математическое моделирование поведения современных антифрикционных полимеров // Прикладная математика и вопросы управления. – 2019. – № 4. – С. 43-56.
Анна Александровна Каменских