КВАЗИПЕРИОДИЧЕСКИЙ РЕЖИМ ТОРМОЖЕНИЯ НЕОДНОРОДНОГО УПРУГОГО ЦИЛИНДРА НА УПРУГОМ ОСНОВАНИИ

Автор: Алёна Николаевна Зотова

Соавторы: А.А. Зобова

Организация: Механико-математический факультет МГУ имени М.В. Ломоносова

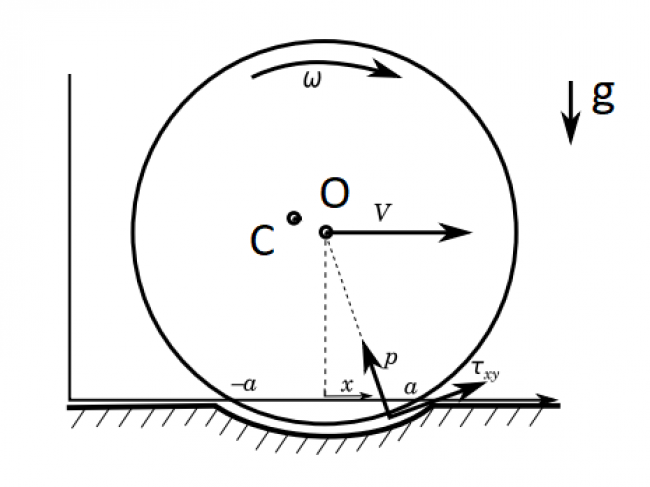
Рассматривается динамическая задача о торможении при качении с проскальзыванием бесконечного неоднородного цилиндра из упругого материала по основанию из того же материала. Ось цилиндра и граница недеформированного основания горизонтальны. Центр масс цилиндра смещен относительно оси цилиндра на малую по сравнению с радиусом цилиндра величину.  Взаимодействие цилиндра и основания описывается моделью Картера, являющейся решением квазистатической задачи теории упругости [1, 2]. Суммарная касательная реакция зависит от относительного проскальзывания,  при малом значении которого возникает сцепление материалов в области контактного взаимодействия, в результате чего суммарная сила трения уменьшается.

Ранее была изучена аналогичная задача для однородного цилиндра [3]. Анализ торможения неоднородного цилиндра был проведен на основании невозмущенного случая с помощью метода малого параметра и теории осреднения.

Аналитически показано, что при достаточно больших значениях угловой скорости цилиндра происходит быстрое убывание проскальзывания к значениям порядка малого параметра аналогично невозмущенной системе. Дальнейшее движение системы -- квазипериодический дрейф вдоль кривой стационарных движений невозмущенной системы.

Изменение среднего периодического движения происходит вследствие диссипации энергии и проявляется при исследовании задачи во втором приближении по малому параметру. Получено автономное дифференциальное уравнение первого порядка, описывающее систематическое изменение периодического движения. Было проведено численное моделирование системы и визуализация полученных результатов. Аналитические выводы полностью подтверждены численным интегрированием полной системы уравнений.

Работа выполнена при поддержке гранта РФФИ №19-01-00140.

[1]   Carter F.W. On the action of a locomotive driving wheel // Proc. R. Soc. A. 1926. V. 112. P. 151—157.

[2]     Горячева И.Г. Механика фрикционного взаимодействия. М.: Наука, 2001. 478 с.

[3]     Горячева И. Г., Зобова А. А. Динамика упругого цилиндра на упругом основании // Прикладная математика и механика. 2019. Т.83 Вып.1. С.39—46.