Метод моментов в задачах математического моделирования полидисперсных систем

Автор: Артур Камилевич Гильфанов

Соавторы: Зарипов Тимур Шамилевич

Организация: Казанский (Приволжский) федеральный университет

Взвешенные в газе частицы представляют собой полидисперсную среду, описывающуюся функцией плотности распределения по фазовым переменным. В случае малых частиц функция плотности является одномерной и характеризуется распределением частиц по размерам. Для частиц крупных размеров дисперсная фаза имеет распределение и по другим переменным: компоненты скорости частиц и др.

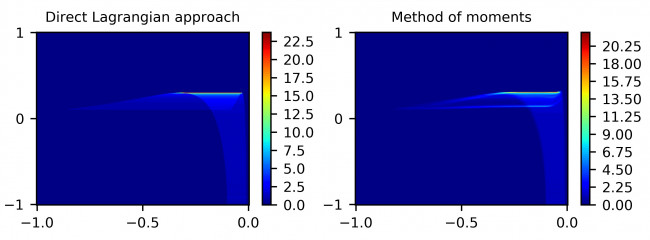
В настоящей работе развит метод условных моментов для моделирования дисперсной фазы, описываемой функцией распределения по двум компонентам скорости в предположении одинакового размера для всех частиц. Моделирование основано на численном решении уравнения Больцмана с учетом силы сопротивления по закону Стокса. Рассмотрены одно-, двух- и трехточечные аппроксимации функции плотности распределения в рамках ее дискретного представления с помощью квадратурных узлов. Модифицирована численная схема расчета адвекции инерционных частиц, гарантирующая физическое правдоподобие аппроксимации функции распределения при решении задачи ее восстановления по значениям моментов. Решена задача о течении инерционных частиц в гиперболическом потоке. Дано сравнение результатов моделирования, полученных методом моментов, прямым лагранжевым и полным лагранжевым подходами. Показано, что одноточечная аппроксимация функции распределения в зоне разворота частиц некорректно учитывает пересечение траекторий, приводящее к схлопыванию потока частиц в этой зоне. Двух- и трехточечные приближения верно отображают образование складки в зоне разворота. Показано, что наилучшее согласие с лагранжевыми подходами дает метод моментов с использованием двухточечной аппроксимации функции распределения. Решена задача о движении инерционных частиц в вихре Ламба. Показано, что метод моментов хорошо предсказывает положение фронта облака частиц, двигающегося от центра вихря, однако значительно занижает значение числовой плотности частиц на фронте. 

Работа выполнена при поддержке Российского фонда фундаментальных исследований (проект № 18-31-00387).