ФГБОУ ВО Пермский национальный исследовательский политехнический университет
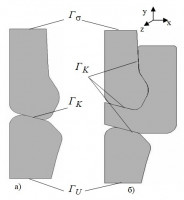
В современной медицине и биомеханике особое внимание уделяется проблемам повышения качества жизни населения. При этом большое количество научных исследований направлено на оптимизацию биомеханических узлов, математическое моделирование их деформационного поведения, а также исследования моделей материалов биомеханических конструкций и определяющих соотношений, описывающих их поведение в процессе деформирования. В данной работе рассмотрено деформирование зубной шины из этиленвинилацетат (Eva) Drufosoft при контактном взаимодействии с зубочелюстной системой человека.
Для моделей с канонической геометрией установлено падение интенсивности напряжений в твердых тканях зубов при их контакте через протетическую конструкцию более чем в 5 раз, чем при контакте без зубной шины. Для модели контакта зубов не канонической формы установлено, что уменьшение интенсивности напряжений для зубов верхнего (более чем в 2 раза) и нижнего зубного ряда (в 0,8 раз) имеет количественное отличие. Для всех вариантов моделей установлены зависимости максимальных интенсивности напряжений в твердых тканях зубов и пластической деформации зубной шины от величины нагрузки.
Анна Александровна Каменских
НИИ механики МГУ
Ветродвигателем называют устройство, преобразующее энергию ветра в энергию вращательного движения главного рабочего органа ветродвигателя -- вертушки. Считается, что первые ветродвигатели появились на Ближнем Востоке, примерно, за 200 лет до н.э. Использовались они для размола зерна. И вот, спустя столько времени человечество продолжает использование ветродвигателей и, кроме того, находит им всё новое и новое применение.
В данной задаче при помощи рассматривается модель катамарана с ветродвигателем. Представлена динамическая модель катамарана. Проведённый анализ показал, что тянущая сила гребного винта может превосходить суммарную силу лобового сопротивления винта и пропеллера, а значит, при установке ветродвигателя на плавающее судно можно ожидать движение любым курсом, с том числе, против ветра.
В настоящей работе представлена динамическая модель системы с ветродвигателем, проведен параметрический анализ модели.
Собраны 2 тестовых варианта катамарана с ветродвигателем:
1) С одним пропеллером и одним винтом, соединёнными валом;
2) С двумя пропеллерами и двумя винтами, подсоединёнными к двум вложенным осям. При этом векторы угловых скоростей вложенных осей противонаправлены.
В силу особенностей конструкции, возможна установка на оси пропеллеров и винтов различной формы.
Проведены серии экспериментов для обоих типов катамарана с различными парами «пропеллер – винт», отличающимися между собой количеством, размером и формой лопастей. Экспериментально определена сила тяги в зависимости от скорости набегающего потока. Наличие установившегося режима движения судна с ветродвигателем подтверждено экспериментально.
Работа выполнена при финансовой поддержке РФФИ (Проект № 17-08-01366).
1. Досаев М.З., Кобрин А.И., Локшин Б.Я., Самсонов В.А., Селюцкий Ю.Д., Селюцкий Ю.Д. Конструктивная теория МВЭУ. Часть I. Москва. Изд-во Моск. ун-та. 2017.
Михаил Андреевич Гарбуз
ФГБОУ ВО Пермский национальный исследовательский политехнический университет
В настоящее время существует большой выбор антифрикционных полимерных материалов российского и зарубежного производства, пригодных в той или иной степени для работы в условиях контактного деформирования в качестве антифрикционных покрытий и прослоек: композиционные материалы на основе фторопласта с различными нанонаполнителями, модифицированный фторопласт, сверхвысокомолекулярные полиэтилены и др. Контактные узлы с антифрикционными покрытиями и прослойками применяются во многих сферах, к таким конструкциям предъявляются повышенные требования относительно прочности, надежности и долговечности, а оптимизация выбора материалов антифрикционного слоя позволит повысить ресурс работы конструкции.
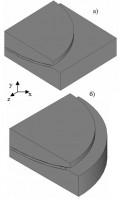
Для эффективного использования антифрикционных полимеров требуется анализ физико-механических, фрикционных, усталостных и эксплуатационных свойств материалов. На базе ПФИЦ УрО РАН д.ф.-м.н. Адамовым А.А. выполнена серия натурных экспериментов, направленная на определение свойств антифрикционных материалов, необходимых для построения математических моделей их поведения.На примере сферической опорной части (рис. 1) с разной геометрией нижней плиты исследовано влияния свойств материалов тонкого антифрикционного слоя на параметры зоны контакта в частности и деформационное поведение конструкции в целом. Реализована трехмерная задача контакта плит опорной части через антифрикционную прослойку с учетом фрикционных свойств материалов, модель включает три контактные поверхности с заранее не известной площадкой контакта и заранее не известным распределением зон контактных состояний [1, 2].
В рамках серии численных экспериментов установлены: зависисмость распределения зон контактных состояний от уровня и вида нагрузки, распределение контактных давления и касательного напряжения для всех вариантов нагружения. При анализе результатов установлено резкое падение контактных напряжений у края прослойки (до 10% общей площади) при действии только вертикальных нагрузок. Зарегистрирована тенденция подъема контактного узла по боковой поверхности опорной части при росте горизонтальных усилий, действующих на конструкцию, что сопровождается негативными эффектами: уменьшением площади полного контактного сцепления поверхностей, ростом площадей скольжения и отлипания, увеличением (до 1,6 раза) максимальных уровней контактного давления.
Анна Александровна Каменских
Лаборатория вибрационной гидромеханики, Пермский государственный гуманитарно-педагогический университет, Пермь
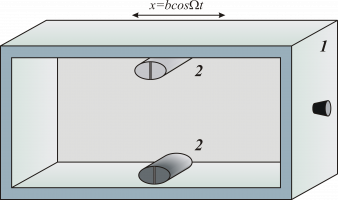
В работе представлены результаты экспериментального исследования вибрационной динамики твердых одиночных и множественных включений в форме эллиптических цилиндров в заполненном вязкой несжимаемой жидкостью прямоугольном контейнере, совершающем поступательные гармонические колебания.
Изучаются особенности поведения тел в зависимости от их относительного размера и плотности, количества тел в объеме жидкости, расстояния между телами и стенкой при различных значениях безразмерной амплитуды и частоты вибраций. Эксперименты проводятся в постановке, ранее описанной авторами в работе [1].
Для выяснения природы взаимодействия тел с границами полости и друг с другом, а также построения траекторий колебаний тел, проводится скоростная видеосъемка процесса с его последующей покадровой обработкой и анализом. С целью изучения структуры осредненных сдвиговых колебаний жидкости применяется P.I.V. методика.
При проведении исследования, наряду с осциллирующим движением тела, особое внимание уделено осредненным эффектам, возбуждаемым в результате колебаний тел в жидкости. В частности, изучению вибрационной подъемной силы, действующей на твердые эллиптические включения в непосредственной близости от твердых границ.
Эксперименты проводятся как с тяжелыми, так и с легкими эллиптическими цилиндрами. Особое внимание уделяется телам с плотностями, мало отличающимися от плотности жидкости, поскольку пробные эксперименты показали, что вибрационная подъемная сила, действующая на тела с относительной плотностью близкой к единице, имеет определенно другую природу, не связанную с инерционными колебаниями включения относительно жидкости.
Результаты исследований обобщаются на плоскости управляющих безразмерных параметров. Исследование проводится при варьировании в широком диапазоне безразмерной частоты и амплитуды вибраций полости. Особое внимание уделено предельному случаю низких безразмерных частот, когда размеры тел оказываются сравнимы с толщиной вязкого пограничного слоя Стокса.
Полученные результаты исследования могут найти активное применение в разработке эффективных методов управления твердыми включениями в вязкой жидкости.
Работа выполнена при финансовой поддержке Российского Научного Фонда (проект 18-71-00122).
1. V.D. Schipitsyn, V.G. Kozlov. Oscillatory and Steady Dynamics of a Cylindrical Body Near the Border of Vibrating Cavity Filled with Liquid // Microgravity Sci. Technol. (2018) 30: 103-112. DOI: https://doi.org/10.1007/s12217-017-9583-4
Виталий Дмитриевич Щипицын
ЦАГИ, МФТИ
Применение научных методов в разработке новых музыкальных инструментов представляет большой практический интерес. Разработана оригинальная концепция нового музыкального инструмента, которая обладает значительными преимуществами в сравнении с аналогами, прототипами и традиционными инструментами. Подготовлены формула изобретения, реферат, выполнен патентный поиск, приведено детальное описание существующих решений. Создана опытная модель нового музыкального инструмента, описаны модификации его конструкции. Уже в таком виде конструкция обладает рядом преимуществ по сравнению с аналогами и прототипами. Приведен обзор существующих решений и описание преимуществ нового инструмента по сравнению с известными аналогами, прототипами и традиционными инструментами. Новый инструмент механический и управляется только за счет действий музыканта.
Иван Алексеевич Амелюшкин
Волгоградский государственный технический университет
В настоящее время потребность в мобильных шагающих роботах достаточно велика. Одной из проблем развития шагающих машин и роботов является характер движения движителей: периодический разгон и торможение неуравновешенных шагающих движителей. Показано, что в таком случае непроизводительные потери энергии пропорциональны квадрату скорости движения корпуса робота, а необходимая для поддержания постоянной скорости движения мощность пропорциональна кубу скорости
Ярослав Владимирович Калинин
ФГБОУ ВО УрГУПС
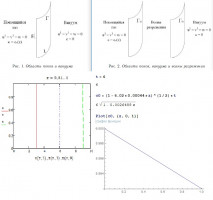
Рассматриваются двумерные изэнтропические течения в условиях действия силы тяжести. В качестве математической модели используется система уравнений газовой динамики. Для постановки задачи о распаде специального разрыва в системе делается вырожденная замена переменных, а именно: зависимые и независимые переменные меняются ролями [1]. В новых переменных для системы ставится начально-краевая задача с данными на звуковой характеристике и дополнительным условием. Доказывается теорема существования и единственности поставленной начально-краевой задачи в окрестности звуковой характеристики. Численно моделируется закон движения звуковой характеристики, отделяющей волну разрежения от неоднородного покоящегося газа.
Далее решение строится в виде степенных рядов. Для определения коэффициентов рядов выписываются и интегрируются системы обыкновенных дифференциальных уравнений. Анализ структуры коэффициентов рядов позволил доказать существование построенного решения в области от звуковой характеристики до границы газ-вакуум включительно. Для определения закона движения границы газ-вакуум выписывается квазилинейная система уравнений с частными производными, которая с помощью характеристического параметра сводится к системе обыкновенных дифференциальных уравнений. Численно моделируется закон движения свободной границы, отделяющей волну разрежения от вакуума.
Анна Сергеевна Кирьянова
МГУ им. М.В. Ломоносова
Рассматривается система уравнений одномерной мелкой воды над неровным дном. Для этой системы уравнений был найден новый закон сохранения, дополнительный к двум основным. Были также найдены все гидродинамические законы сохранения и симметрии для произвольных профилей дна. Система уравнений одномерной мелкой воды над наклонным дном связана точечным преобразованием с линейной системой уравнений, которая может быть получена из исходной формальным отбрасыванием нелинейных слагаемых. В данной работе рассматривается класс алгебраических точных решений линеаризованной системы уравнений одномерной мелкой воды над наклонным дном, который позволяет получить класс точных решений нелинейной мелкой воды с помощью этого преобразования. Описаны эффекты заплеска и усиления амплитуды при отражении волны от берега.
Константин Павлович Дружков
Казанский (Приволжский) федеральный университет
Взвешенные в газе частицы представляют собой полидисперсную среду, описывающуюся функцией плотности распределения по фазовым переменным. В случае малых частиц функция плотности является одномерной и характеризуется распределением частиц по размерам. Для частиц крупных размеров дисперсная фаза имеет распределение и по другим переменным: компоненты скорости частиц и др.
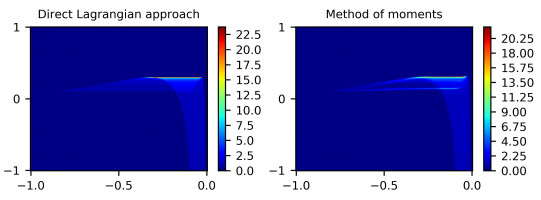
В настоящей работе развит метод условных моментов для моделирования дисперсной фазы, описываемой функцией распределения по двум компонентам скорости в предположении одинакового размера для всех частиц. Моделирование основано на численном решении уравнения Больцмана с учетом силы сопротивления по закону Стокса. Рассмотрены одно-, двух- и трехточечные аппроксимации функции плотности распределения в рамках ее дискретного представления с помощью квадратурных узлов. Модифицирована численная схема расчета адвекции инерционных частиц, гарантирующая физическое правдоподобие аппроксимации функции распределения при решении задачи ее восстановления по значениям моментов. Решена задача о течении инерционных частиц в гиперболическом потоке. Дано сравнение результатов моделирования, полученных методом моментов, прямым лагранжевым и полным лагранжевым подходами. Показано, что одноточечная аппроксимация функции распределения в зоне разворота частиц некорректно учитывает пересечение траекторий, приводящее к схлопыванию потока частиц в этой зоне. Двух- и трехточечные приближения верно отображают образование складки в зоне разворота. Показано, что наилучшее согласие с лагранжевыми подходами дает метод моментов с использованием двухточечной аппроксимации функции распределения. Решена задача о движении инерционных частиц в вихре Ламба. Показано, что метод моментов хорошо предсказывает положение фронта облака частиц, двигающегося от центра вихря, однако значительно занижает значение числовой плотности частиц на фронте.
Работа выполнена при поддержке Российского фонда фундаментальных исследований (проект № 18-31-00387).
Артур Камилевич Гильфанов
Федерального государственного бюджетного образовательного учреждения высшего образования «Комсомольский-на-Амуре государственный университет»

В последнее время в авиастроении в качестве деталей все больше применяются крупногабаритные монолитные и монолитно-сборные панели, которые позволяют повысить прочность и жесткость конструкций с одновременным снижением массы и улучшением аэродинамических характеристик. Задание аэродинамической формы таких монолитных панелей проводится процессами формообразования, осуществляющихся в режимах пластического деформирования, как при обычных, так и при повышенных температурах [1]. Формирование в режиме ползучести и при напряжениях, не превышающих предела упругости материала, обеспечивает более высокий остаточный прочностной ресурс по сравнению с методом обычной холодной штамповки [2]. Экспериментальные результаты позволяют отождествить работу рассеяния с параметром поврежденности [2]. В этом случае процессы формообразования позволяют управлять уровнем поврежденности материала, согласовывать с технологическими ограничениями, за счет оптимального выбора пути деформирования во времени [3].
В качестве примера, рассматривается формование изделий из листов и панелей, с помощью реконфигурируемого стержневого пуансона (матрицы), позволяющего изменять форму заготовки. Точность формы и качество детали, полученной технологиями обработки материалов давлением при заданных параметрах процесса, зависит от точности вычисленной формы оснастки с законом изменения в процессе деформирования, задающей упреждающую форму (рис.1.). Упреждающая форма должна обеспечивать заданную остаточную кривизну панели после освобождения ее от силовой оснастки.
Задача деформирования в ползучести c контактными условиями решается методом конечных элементов. В качестве критерия оптимизации принимается накопленная в процессе деформирования работа рассеяния. Учитывая дискретные по времени уравнения пошаговой процедуры интегрирования и минимизируемую функцию, формулируется дискретная задача оптимального управления. Данная задача решается методом динамического программирования.
Таким образом, разработанный численный метод позволяет находить рациональные процессы формообразования не только для идеальной пластинки или оболочки, но и для таких деталей, как панели крыла.
Работа выполнена при финансовой поддержке РФФИ (16-31-60038 мол_а_дк), совета по грантам Президента РФ (МД-4117.2018.1).
1. Аннин Б.Д., Олейников А.И., Бормотин К.С. Моделирование процессов формообразования панелей крыла самолета SSJ-100 // Прикладная механика и техническая физика. 2010. Т.51. №4. С. 155-165.
2. Соснин О.В., Никитенко А.Ф., Горев Б.В. К обоснованию энергетического варианта теории ползучести и длительной прочности металлов // Прикладная механика и техническая физика. 2010. 51. № 4. 188–197.
3. Бормотин К.С., Олейников А.И. Вариационные принципы и оптимальные решения обратных задач изгиба пластин при ползучести // Прикладная механика и техническая физика. 2012. № 5. 136–146.
Константин Сергеевич Бормотин
ООО "Вычислительная инженерная платформа"
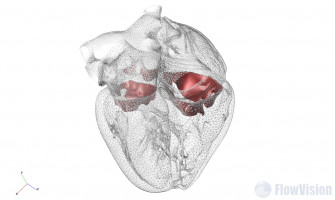
Проект «Живое сердце» - международный проект SIMULIA, в который вовлечены инженеры, медики и ученые со всего мира для работы над реалистичным моделью сердца. Предполагается, что эта модель будет применяться в образовании, конструировании медицинских аппаратов, клинической диагностики реального сердца, а также тестировании уже существующих и будущих инновационных решений, призванных значительно улучшить жизнь человека, страдающего различными пороками сердца.
При разработке стентов, искуственных клапанов или планировании операций на сердце, необходимо моделировать нагруженное состояние устройств и приборов в сложнызх нестационарных условиях. Применение программных комлпексов Abaqus-FlowVision позволяет наиболее точно предсказать поведение перспективного устройства под дейтсвием сложной гидродинамической нагрузки.
Владимир Сергеевич Каширин
ННГУ им. Н. И. Лобачевского
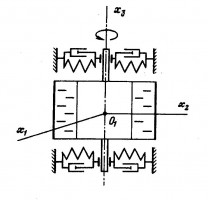
Исследование устойчивости стационарного вращения роторных систем с жидкостью представляет интерес как с общетеоретической, так и с прикладной точек зрения. Ранее был разработан оригинальный метод исследования устойчивости таких систем [1]. Предполагалось, что ось вращения ротора расположена в изотропных вязкоупругих закреплениях, а угловая скорость вращения поддерживается постоянной. В дальнейшем метод удалось обобщить и распространить на системы с анизотропными закреплениями оси ротора [2]. В работе [2] установлено влияние анизотропии жесткости закреплений оси ротора на форму границ областей устойчивости в пространстве параметров.
В данной работе исследуется устойчивость режима стационарного вращения типичной роторной системы с жидкостью, имеющей вязкоупругие закрепления оси ротора с анизотропией сил вязкости. Приведены примеры построения границ областей устойчивости в пространстве параметров и отмечено возникновение механических эффектов, вызванных анизотропией закреплений оси ротора.
1. Дерендяев H.В. Устойчивость вращения роторных систем, cодержащих жидкость: Монография. - Нижний Новгород: Изд-во Нижегородского госуниверситета, 2014.- 154 с.
2. Дерендяев Н. В., Дерендяев Д. Н. Исследование устойчивости стационарного вращения роторных систем с жидкостью. Труды Международной научной конференции «Фундаментальные и прикладные задачи механики». – Москва: изд-во МГТУ им. Н. Э. Баумана, 2017.- 222 с.
Дмитрий Николаевич Дерендяев
Московский Государственный Университет имени М.В. Ломоносова
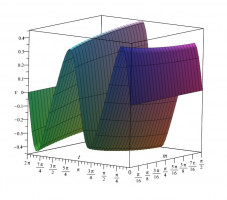
Рассматривается одномерное адиабатическое движение с плоскими волнами совершенного идеального газа в лагранжевых переменных. При этом уравнения движения сводятся с использованием массовой переменной к системе с квадратичной нелинейностью. Решение ищется, в частности, в виде рядов для закона движения газа и давления по степеням косинуса от временной переменной с коэффициентами, зависящими от массы. Для построения ряда требуется задать три первых коэффициента. Все остальные коэффициенты вычисляются рекуррентным образом по заданным при условии ненулевой производной первого коэффициента ряда для закона движения. Преимуществом данного подхода перед разложением решения, например в тригонометрический ряд Фурье, является именно конечность алгебраических рекуррентных соотношений, связанных только с вычислением производных по массе. Проводятся численные расчеты, которые показывают высокую сходимость ряда при определенных ограничениях на производные от задаваемых коэффициентов. Дальнейшим обобщением развитого подхода является представление решения в виде суммы одного ряда по степеням косинуса и произведения синуса на другой аналогичный ряд. При этом условием рекуррентной разрешимости является неравенство нулю разности квадратов производных первых членов, указанных выше рядов. Развивается соответствующий вычислительный процесс. Приводятся примеры, не содержащие особенностей.
Работа частично поддержана РФФИ (проект 17-01-00037)
Рис. Пример графика скорости потока на периоде
Дмитрий Владимирович Украинский
НИИ механики МГУ
Моделирование турбулентных течений жидкости и газа, вероятно, является одной из наиболее распространенных прикладных задач математической физики, для решения которых применяются суперкомпьютеры. Использование вихреразрешающих методов позволяет получить высокую точность результатов моделирования, однако требует больших расчетных сеток и длительных расчетов по времени для набора турбулентной статистики. Одним из способов повышения эффективности таких расчетов является использование алгоритма расчета турбулентных течений, предложенного в [1] и [2], который сочетает традиционный подход на основе осреднения по времени с усреднением по ансамблю реализаций этого течения. Это позволяет уменьшить длину интервала набора статистики для каждой из реализаций и заменить один длительный расчет на расчеты нескольких более коротких интервалов интегрирования по времени.
Особенностью данного алгоритма является необходимость генерации множества некоррелированных статистически стационарных турбулентных полей, используемых в качестве начальных данных при осреднении. Простейшим способом решения данной проблемы является моделирование процесса перестроения течения и выхода на турбулентный режим для различных начальных данных. Этот подход на практике обеспечивает некоррелированность полей скоростей, но требует значительных вычислительных затрат, сокращая преимущества метода. В настоящей работе предлагается оптимизированный способ генерации начальных турбулентных полей, основанный на внесении случайных возмущений в процессе выхода течения на турбулентный режим. Обсуждается область применимости данного подхода и возможное ускорение расчета. Полученные оценки подтверждаются результатами численных расчетов, которые демонстрируют существенное расширение области применимости метода и 10-20% повышение эффективности расчетов в целом.
Работа частично поддержана грантом РФФИ 17-01-00140-а. Для расчетов использовалось оборудование Центра коллективного пользования сверхвысокопроизводительными вычислительными ресурсами МГУ имени М.В. Ломоносова.
1. Makarashvili V., Merzari E., Obabko A., Siegel A., Fischer P. A performance analysis of ensemble averaging for high fidelity turbulence simulations at the strong scaling limit // Computer Physics Communications, vol. 219, p. 236-245, 2017. doi: 10.1016/j.cpc.2017.05.023
2. Krasnopolsky B. An Approach for Accelerating Incompressible Turbulent Flow Simulations Based on Simultaneous Modelling of Multiple Ensembles // Computer Physics Communications, 2018. doi:10.1016/j.cpc.2018.03.023
Борис Иосифович Краснопольский
НИИ механики МГУ
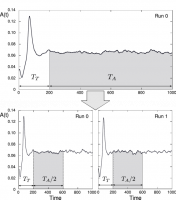
Рост потенциала высокопроизводительных вычислительных систем открывает новые возможности в плане разработки перспективных численных методов для решения задач математической физики. Одними из приложений, где оказываются востребованными высокопроизводительные вычисления, являются задачи моделирования турбулентных течений в рамках вихреразрешающих методов. В [1, 2] был предложен новый подход ускорения расчетов статистически стационарных турбулентных течений, основанный на комбинации осреднения по времени и по ансамблю независимых реализаций одного и того же турбулентного течения. Указанный подход позволяет сократить длительность расчета для каждого из состояний, и, в некотором смысле, распараллелить вычисления по времени.
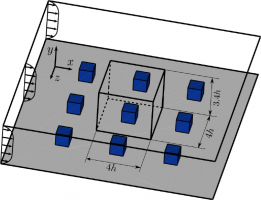
В работах [1] и [2] были использованы различные стратегии для расчета множества состояний течения. В [1] предлагается проводить расчет каждого состояния независимо, и ускорять расчет за счет увеличения количества вычислительных устройств. В [2], наоборот, все расчеты выполняются в рамках одного запуска на заданном количестве вычислительных ресурсов, а ускорение времени решения задачи достигается за счет повышения вычислительной эффективности используемых численных методов. Вообще говоря, указанные публикации реализуют два предельных случая более общей схемы, сочетающей расчет нескольких состояний в рамках нескольких независимых расчетов. В настоящем докладе рассматривается обобщенная расчетная схема и предлагается критерий выбора оптимальной конфигурации расчета [3]. Предложенные теоретические оценки сопоставляются с результатами численных экспериментов, проведенных на примере задачи об обтекании турбулентным потоком массива кубов, расположенных на стенке плоского канала.
Работа частично поддержана грантом РФФИ 17-01-00140-а. Для расчетов использовалось оборудование Центра коллективного пользования сверхвысокопроизводительными вычислительными ресурсами МГУ имени М.В. Ломоносова.
1. Makarashvili V., Merzari E., Obabko A., Siegel A., Fischer P. A performance analysis of ensemble averaging for high fidelity turbulence simulations at the strong scaling limit // Computer Physics Communications, vol. 219, p. 236-245, 2017. doi: 10.1016/j.cpc.2017.05.023
2. Krasnopolsky B. An Approach for Accelerating Incompressible Turbulent Flow Simulations Based on Simultaneous Modelling of Multiple Ensembles // Computer Physics Communications, 2018. doi:10.1016/j.cpc.2018.03.023
3. Krasnopolsky B. Optimal strategy for modelling turbulent flows with ensemble averaging on high performance computing systems // Lobachevskii Journal of Mathematics, vol. 39, № 4, p. 533-542, 2018. doi: 10.1134/S199508021804008X
Борис Иосифович Краснопольский