СРАВНЕНИЕ ВОЗДУШНО-РЕАКТИВНЫХ ДВИГАТЕЛЕЙ С МЕДЛЕННЫМ ГОРЕНИЕМ И ГОРЕНИЕМ В ДЕТОНАЦИОННЫХ ВОЛНАХ

Автор: Александр Николаевич Крайко

Организация: Центральный институт авиационного моторостроения имени П.И. Баранова

Выполнено сравнение термических коэффициентов полезного действия и удельных тяг и импульсов прямоточных реактивных двигателей разных типов с медленным ("дефлаграционным") горением (МГ) и с горением в движущихся (пульсирующих и вращающихся – «спиновых») и неподвижных детонационных волнах (ДВ). Актуальность такого сравнения обусловлена распространенными, особенно в последнее время, утверждениями о возможном увеличении тяговых характеристик воздушно-реактивных двигателей (ВРД) с горением в ДВ (в первую очередь, в пульсирующих – PDE и вращающихся – RDE) на десятки процентов в сравнении с прямоточными ВРД (ПВРД) с МГ при постоянном давлении в дозвуковом потоке. Подобные прогнозы, однако, опираются не на прямой расчет тяг этих двигателей, а на сравнение их идеальных термических коэффициентов полезного действия (кпд) – h_th и на применимые только к стационарным течениям в инерциальных системах координат формулы, связывающие также идеальные удельные тяги и импульсы с идеальными кпд. Для PDE эти формулы неверны из-за нестационарности течения.

В России утверждения о преимуществах детонационного горения (ДГ) нередко сопровождаются ссылками на заметку Я.Б. Зельдовича [1] 1940 г., переведенную на Западе только в начале XXI века. Для незнакомых с этой заметкой ссылки на столь авторитетного ученого производят требуемый эффект в противоположность тому, что писал сам автор. Хотя Я.Б. Зельдович обнаружил некоторое увеличение термического коэффициента полезного действия (КПД) при ДГ, это не вызвало у него эйфории. Напротив, в той же заметке высказаны только скептические соображения о применении ДГ, например: "... поиски циклов с ДГ в погоне за небольшим увеличением принципиально достижимого кпд бесперспективны". Ни в этой, ни в других публикациях Я.Б. Зельдовича высказываний в поддержку ДГ нет.

В развитие [1, 2] выполнен термодинамический анализ разных типов ВРД с ДГ и МГ. В исследуемых далее ВРД горению почти всегда предшествует сжатие в воздухозаборнике поступающего из атмосферы со скоростью V₀ воздуха и всегда заканчивается "расчетным" расширением в сопле продуктов сгорания до давления набегающего потока р₀. В рассматриваемых моделях двигателей предварительное сжатие воздуха в воздухозаборнике и расширение продуктов сгорания в сопле принимаются изэнтропическими и стационарными. По определенным, как в [2], идеальным термическим кпд (h_th) находится отношение V_e/V₀, где V_e – скорость на выходе из сопла при расчетном расширении до р₀. Удельные тяга и импульс пропорциональны разности (V_e/V₀ – 1). Рассмотренные типы ВРД включают двигатели с МГ при постоянном давлении, как в ПВРД (по циклу Брайтона), и постоянном объеме (по циклу Хэмфри), пульсирующие детонационные двигатели (PDE) с горением в ДВ Чепмена - Жуге (ДВ_CJ), ВРД с горением в стационарных ДВ_CJ, в том числе, с предварительным торможением сверхзвукового потока (SDE_y³1, y = Т₃/Т₀, Т₀ и Т₃ – температуры холодного воздуха и горючей смеси перед ДВ) и в косой ДВ – SDE_OSW (при y = 1).

При фиксированных показателях адиабаты воздуха, горючей смеси и продуктов сгорания идеальные характеристики рассмотренных ВРД, предполагающие, как в [2], отсутствие потерь при торможении воздуха в воздухозаборнике, его смешении с газообразным топливом и истечении продуктов сгорания из реактивного сопла, зависят от двух безразмерных параметров: числа Маха полета М₀ и q° = q/(c_pT₀) – безразмерной теплотворной способности горючей смеси (с_р – теплоемкость при постоянном давлении). При q° = 6 и 9 сравнение идеальных кпд h_th и рассчитанных по h_th с помощью упомянутых выше формул (незаконных для PDE) идеальных удельных тяг и импульсов всех рассмотренных двигателей выполнено для М₀ от 0.3 до 8. Для этих q° и М₀ по такой идеальной тяге PDE незначительно превосходит ВРД с горением при постоянном объеме (по циклу Хэмфри), а ПВРД с МГ – намного только при М₀ < 1.5. С ростом М₀ превышение идеальной тяги PDE над идеальными тягами других ВРД за исключением SDE_OSW быстро уменьшается. Так, при q° = 6 и 9 превосходство по идеальной тяге PDE над остальными становится малым при увеличении числа Маха полета М₀.

Пусть PDE имеет n цилиндрических, синхронно работающих групп детонационных камер (ДК) с мгновенно открывающимися и закрывающимися клапанами (входными силовыми стенками). При открытых клапанах в ДК поступает идеально перемешанная горючая смесь. Период работы одной ДК PDE можно разбить на несколько этапов: 1. Открытие клапана, заполнение ДК горючей смесью, мгновенные закрытие клапана и инициирование ДВ волны у входного конца ДК; 2. Приход ДВ на правый конец ДК – сечение входа в идеально регулируемое реактивное сопло; 3. ДВ отражается от правого частично открытого сечения ДК (сужения сопла) как ударная волна (УВ), которая движется к закрытому входному сечению ДК. Далее нестационарные ударные волны, двигаясь по ДК, могут несколько раз отразиться от ее концов. Несмотря на затухание, отражающиеся УВ – не учитываемый при определении идеальных характеристик PDE источник роста энтропии. Клапан мгновенно открывается, когда среднее давление продуктов сгорания в ДК становится меньше давления заторможенного воздуха и идеально перемешанного с ним топлива в объеме перед клапаном.

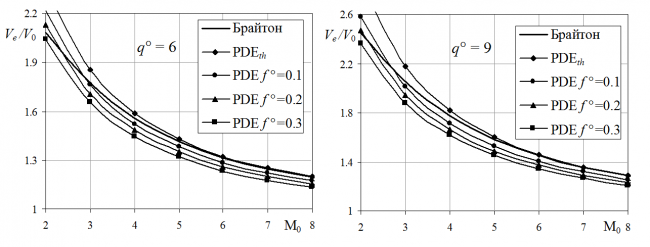
Истечение продуктов сгорания происходит на протяжении всего цикла работы PDE. Течение в расширяющейся части сопла квазистационарное и изэнтропическое, площадь выходного сечения сопла идеально регулируемая. Расчёты проводились в рамках одномерной задачи в приближении уравнений Эйлера. Система уравнений одномерной нестационарной газовой динамики численно решалась с помощью явной монотонной распадной разностной схемы второго порядка (для гладких решений) по пространственной координате х и по времени t. Второй порядок по времени обеспечивался привлечением схемы Рунге - Кутты. При заданных f ° (отношении площади критического сечения сопла к площади поперечного сечения ДК), М₀ и q° в течении периода работы ДК PDE отношение скоростей V_e/V₀ получается как функция времени. Его интегрирование по периоду дает средние значения V_e/V₀ и тяговые характеристики с учетом нестационарности и неизэнтропичности течения продуктов сгорания в детонационной камере.

На рисунке приведены кривые отношений V_e/V₀ для ПВРД (цикл Брайтона, от времени не зависит) и для PDE: посчитанных по идеальному термическому кпд (PDE_th) и для нескольких значений f °, найденных в рамках описанной выше нестационарной модели. Видно, что в типичных ситуациях ПВРД лучше многокамерных PDE с вращающимся клапаном (для f °= 0.3 и 0.1 – при М₀ ³ 2 и М₀ ³ 3). Согласно [3] тяговые характеристики ПВРД заведомо лучше тяговых характеристик и однокамерного PDE, предложенного в [4]. По этим характеристикам уступают ПВРД и все рассмотренные выше ВРД с горением в стационарных ДВ. Из еще не рассмотренных "детонационных" ВРД в последнее время особое внимание уделяется двигателям с вращающейся или спиновой ДВ (RDE). Одно из объяснений такого внимания – переход к стационарному течению во вращающейся со скоростью ДВ системе координат и последующие рассуждения с сохраняющейся в стационарных потоках полной энтальпией. При этом, правда, забывают, что в координатах, вращающихся с угловой скоростью w, вдоль линий тока сохраняется не "обычная" полная энтальпия H, а разность H °= H – (wr)²/2. В кольцевой камере сгорания RDE произведение wr равно скорости детонационной волны. Поэтому величина w так велика, что любые изменения радиальной координаты r при истечении продуктов сгорания заведомо исключают возможность определения отношения V_e/V₀ через h_th ВРД с ДГ. В противоположность этому, в силу сохранения H  удельный импульс I_sp RDE с сужающимся центральным телом и цилиндрической "внешней" образующей сопла заметно уменьшится. То что это так, подтверждают низкие значения I_sp, рассчитанные в [5] для четырех вариантов RDE, летящих с М₀ = 5 в однородной стехиометрической смеси водорода и воздуха с параметрами атмосферы Земли на высоте 20 км. Эти значения I_sp = 1990, 2350, 2300 и 2250 с "традиционно" для авторов [5] (см. [3]) завышены: определяя I_sp, они почему-то не учитывают сопротивления наветренной части центрального тела воздухозаборника. Исправленные значения I_sp близки к 1420, 1830, 1780 и 1720 с, однако даже завышенные величины I_sp заметно меньше I_sp ПВРД, который при тех же условиях по оценке авторов [3] равен 3500¸3900 с. Дополнительное возрастание энтропии в RDE также имеет место – в УВ, примыкающей к ДВ на границе свежей горючей смеси и продуктов сгорания. Правда, интенсивность этой УВ невелика.

Итак, утверждения о возможном увеличении тяговых характеристик ВРД на десятки процентов благодаря использованию ДГ необоснованны. Даже для дозвуковых и малых сверхзвуковых чисел Маха полета, на которых ВРД с МГ может по тяговым характеристикам уступать PDE, последние заведомо уступают ТРД с МГ. Поэтому преимущества ВРД с ДГ, если и возможно, то не по тяговым характеристикам, а по простоте конструкции (как при малых М₀ по сравнению с ТРД) или по меньшей теплонапряженности тракта двигателя (напротив, при больших сверхзвуковых числах Маха М₀ > 5 в сравнении c пульсирующим детонационно-дефлаграционным двигателем [6]).

Работа выполнена при поддержке РФФИ (проект 17-01-00126).

Рисунок: кривые V_e/V₀ ПВРД (цикл Брайтона) и PDE, рассчитанные по идеальному кпд (PDE_th) и по нестационарной модели

1.      Зельдович Я.Б. К вопросу об энергетическом использовании детонационного горения // ЖТФ. 1940. Т. 10. Вып. 17. С. 1453-1461.

2.      Heiser W.H., Pratt D.T. Thermodynamic Cycle Analysis of Pulse Detonation Engines // J. of Propulsion and Power. 2002. V. 18. No. 1. P. 68-76.

3.      Егорян А.Д., Крайко А.Н., Пьянков К.С., Тишин А.П. О расчете характеристик импульсного детонационного двигателя и их сравнении с характеристиками ПВРД // Теплофизика и аэромеханика. 2016. Т. 23. № 2. С. 307-310.

4.      Remeev N.Kh., Vlasenko V.V., Khakimov R.A. Analysis of operation process and possible performance of the supersonic ramjet-type pulse detonation engine // Pulse and continuous detonation propulsion / Eds. G. Roy, S. Frolov. Moskow: TORUS PRESS, 2006. P. 235-250.

5.      Дубровский А.В., Иванов В.С., Зангиев А.Э., Фролов С.М. Трехмерное численное моделирование характеристик прямоточной воздушно-реактивной силовой установки с непрерывно-детонационной камерой сгорания в условиях сверхзвукового полета // Химическая физика. 2016. Т. 35. № 6. С. 49-63. 

6.      Крайко А.Н., Александров В.Ю., Александров В.Г. и др. Способ организации горения топлива и детонационно-дефлаграционный пульсирующий прямоточный воздушно-реактивный двигатель. 2016. Патент РФ № 2585328.